Решение

1. Определяем минимальные моменты инерции сечений первой и вто­
рой тяг. I_min= b · h³ /12 = 10 · 0,53 / 12 = 0,1 мм⁴

Сечение второй тяги состоит из трех частей – двух одинаковых прямо­угольников 1 (2,645 ´ 0,5) и половины кольца 2 диаметром d =3мм :

I_(min)2= 2I₁+I₂= 2 · 2,645 · 0,5³/12 + 0,5 p(3)⁴/64 = 0,055+1,98 = 2,04 мм⁴ (считаем, что нейтральная ось сечения совпадает с осью симметрии прямоугольников).

2. Определяем критические напряжения по формуле (7.4):

минимальные радиусы инерции:

, ;

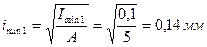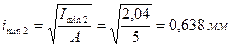гибкости тяг:

, ;

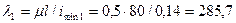критические напряжения:

, ;

3. Поскольку s_кр1 < s_т , первая тяга потеряет устойчивость при s_кр =24,2 МПа, поэтому предельное значение сжимающей силы F_max1 опре­делим из условия проверки на устойчивость (7.6):

F_max1 £ s_кр ×А / [n]= 24,2 × 5 / 1,5 = 80,6 Н.

Принимаем F_max1 = 80 Н.

У второй тяги s_кр2 > s_т, поэтому прежде чем потерять устойчивость, она подвергнется пластической деформации, то есть потеряет прочность. Из условий прочности согласно уравнению (2.7) получим:

F_max2 £ s_кр ×А / [n] = 490 × 5 / 1,5 = 1633 Н.

Принимаем F_max2 =1600 Н.

Вывод : Изменение профиля тяги согласно рис7.3 (что легко можно осу­ществить, например, штамповкой) позволит увеличить величину пре­дельной сжимающей силы в 20(!) раз , причем в первом случае можно опасаться потери устойчивости , а во втором – прочности.

 

8. Сложное сопротивление

 

8.1. Общие сведения. Понятия о теориях прочности

 

Во всех вышерассмотренных случаях в поперечных сечениях деталей под воздействием внешних нагрузок возникало только одно внутреннее усилие: либо продольная сила, либо крутящий или изгибающий момент. Исключение составил лишь плоский поперечный изгиб, когда в поперечных сечениях балки возникают два внутренних усилия — изгибающий момент и поперечная сила. Но и в этом случае при расчете на прочность и жесткость обычно учи­тывают только изгибающий момент.

 

На практике часто встречаются более сложные деформации, когда в попе­речных сечениях действуют два, три и более внутренних усилия одновре­менно. Эти случаи называются сложным сопротивлением.

Порядок решения таких задач:

1) с помощью метода сечений определяют внутренние силовые факто­ры, возникающие в поперечных сечениях стержня (балки, вала);

2) строят эпюры внутренних усилий, позволяющие определить коор­динаты опасного сечения (в ряде случаев двух и более), где внут­ренние усилия максимальны;

3) в опасных сечениях на основании принципа независимости действия сил определяют нормальные и касательные напряжения от каждого внутреннего усилия отдельно;

4) исследуя распределение напряжений по сечению, устанавливают опасные участки (линии, точки), для которых и составляют условие прочности;

5) если окажется, что в опасном участке имеется одноосное напряжен­ное состояние (например, при растяжении и изгибе), то при расчете на прочность сравнивают суммарное нормальное напряжение с до­пускаемым простым, например растягивающим или изгибающим. Если напряженное состояние в точке двухосное (например, кручение и изгиб), расчет выполняют, используя ту или иную теорию (гипоте­зу) прочности.

Суть теорий прочности заключается в том, что при расчете сложных на­пряженных состояний их комбинация условно заменяется одной простой де­формацией, равноопасной (эквивалентной) сложной. В курсе «Сопротивле­ние материалов» рассматриваются такие теории, как «теория наибольших нормальных напряжений», «теория наибольших деформаций», «теория наи­больших касательных напряжений». В «Технической механике» для расчетов деталей авиационных механизмов применяется в основном четвертая, энер­гетическая теория прочности. Согласно этой теории два напряженных со­стояния детали - сложное и эквивалентное ему простое считаются равно-опасными, если равны удельные потенциальные энергии изменения их формы. В основном эта теория применяется при расчетах деталей из пластичных материалов.

 

8.2. Изгиб с растяжением или сжатием

 

Рассмотрим консольную балку длиной l прямоугольного сечения b´ h (рис. 8.1, а), которая подвергается осевому растяжению силой F_х и плоскому поперечному изгибу от силы F_Z.

Задачу определения опасного сечения и дальнейшие расчеты на прочность проведем с помощью принципа независимости действия сил. Согласно этому принципу рассмотрим отдельно изгиб и растяжение. Построим эпюры изгибающих моментов М_и и продольных сил N (рис. 8.1, б).

 

sр

sи

Fz

D

z

 

Рис 8.1

 

Из эпюр видно, что наибольших значений изгибающий момент М_и достигает в сечении АВСD, где он равен F_Zl, а значение продольной силы N = F_х постоянно по всей длине балки. Эпюры напряжений от изгиба s_и и от растяжения в се­чении АВСD показаны на рис. 8.1,в. Как видно, наибольшего значения на­пряжение s_и достигает в слоях АD и ВС, наиболее удаленных от нейтраль­ной оси: s_и = М_и/W_у = F_Zl/(bh²/6). Напряжение s_р одинаково в любом сечении и равно s_р = N / А = F_x / bh.

Нормальные напряжения s_и и s_р, направленные по одной прямой, можно складывать алгебраически. Очевидно, что в итоге наиболее опасным будет сечение в заделке, а в нем наиболее опасным является слой АD, где напряжения s_и и s_р имеют одинаковый знак. Условие прочности балки при этом бу­дет иметь вид:

s_э =s_и + s_р = М_и / W_у+ F_х / А £ [s_и], (8.1)

где s_э - эквивалентное напряжение.

Если сила F_х будет сжимающей, уравнение прочности не изменится, на­пряжения s_и и s_р также будут складываться, но опасным будет слой ВС. По той же причине не имеет значения направление силы F_Z, т.е. знак момен­та М_и в уравнении (8.1) также берется по абсолютной величине.

 

8.3. Косой изгиб (изгиб в двух плоскостях)

 

Изгиб называется косым, если плоскость деформации (расположения изо­гнутой оси балки) не совпадает с плоскостью действия внешних сил и мо­ментов.

Пусть на балку действует сила F, составляющая угол a с осью симметрии сечения z (рис. 8.2, а).

 

 

		Рис 8.2

 

Балка имеет прямоугольное сечение, в котором высота h больше ширины b, вследствие чего и осевые моменты инерции сечения различны:

J_у = bh³/12 >J_z = hb³/12.

В данном случае наибольшие напряжения возникают в точках поперечно­го сечения, наиболее удаленных от нейтральной оси, где напряжение равно нулю. Для определения значений наибольших напряжений в опасном сече­нии АВСД сила F раскладывается на две составляющие — горизонтальную F_у и вертикальную F_Z по направлениям главных осей инерции сечения (рис 8.2, а). В этом случае эпюры напряжений s _гор в горизонтальной и s _верт в вертикальной плоскостях строятся на основании правил и формул, получен­ных ранее для плоского поперечного изгиба (рис. 8.2, б). Максимальные на­пряжения будут в точках опасного сечения, наиболее удаленных от соответствующих нейтральных осей. Так как растягивающим напряжениям припи­сывается знак плюс, а сжимающим - знак минус, то нетрудно увидеть из рис. 8.2, б, что наиболее напряженными будут точки В и Д сечения. Возникаю­щие в них напряжения s_верт и s_гор согласно принципу независимости дейст­вия сил суммируются. Таким образом в рассмотренном случае косого изгиба балки прямоугольного сечения условие прочности в опасном сечении приоб­ретает вид:

(8.2)

 

 

8.4. Изгиб и кручение

 

При нагружении круглого бруса (вала) крутящим М_кр и изгибающим М_и моментами эквивалентное напряжение в рассматриваемом сечении определя­ется на основании энергетической теории прочности при статическом нагру­жении по формуле

(8.3)

Учитывая, что W_р = 2W_у ,получим условия прочности в виде

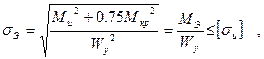(8.4)

где М_Э =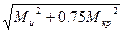 - эквивалентный момент.

При переменных нагрузках проверку на прочность проводят по формуле

(8.5)

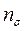где и 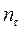- расчетные значения запасов прочности по нормальным и каса­тельным напряжениям (более подробно см. раздел «Переменные напряже­ния»)

 

8.5. Расчет тонкостенных сосудов

 

К тонкостенным сосудам относятся емкости для хранения жидкостей и га­зов, элементы теплообменников, трубопроводов, регуляторов давления, сильфонов, толщина стенок которых не превышает 0,1 минимального радиу­са кривизны. Конструктивные исполнения тонких сосудов может быть раз­личное, а методика расчета на прочность отличается незначительно.

Если сосуды имеют форму тел вращения, то без большой погрешности можно принять, что в стенках возникают только нормальные напряжения (растягивающие или сжимающие) и что эти напряжения распределены рав­номерно по толщине стенки.

Рассмотрим тонкостенный сосуд с толщиной стенки t, находящийся под внутренним давлением р (рис. 8.3).

Вырежем из его стенки элемент площадью dА = d1₁d1₂, радиусы кривизны поверхности сосуда в данном месте r₁ и r₂.

Используя метод сечений, заменим взаимодействие элемента dA c остав­шейся частью сосуда внутренними силами N₁ и N₂, интенсивность которых равна s₁ и s₂. Составим условие статического равновесия элемента, для чего спроецируем силы, действующие на элемент, на направление нормали п - п к поверхности элемента.

Внешняя сила N от внутреннего давления р будет равна N = рdА = рdl₁dl₂ .

Проекция на нормаль п - п внутренних сил N₁ и N₂, действующих попар­но на четырех гранях, равна 2N₁sin(dj ₁/2)+ 2N₂sin(dj ₂/2)=2s₁A₁sin(dj ₁/2)+ +2s₂A₂sin(dj ₂/2).

С учетом ма­лости размеров элемента dА примем sin(dj ₁/2)= dj ₁/2, a sin(dj ₂/2)= dj ₂/2.

Тогда уравнение равновесия элемента записывается в виде

рdl₁dl₂ = 2s₁ A₁ dj ₁ / 2+2s₂ A₂ dj ₂/2=s₁ A₁ dj ₁+ s₂ A₂ dj ₂.

 

 

Из условия dl₁ = r₁dj ₁, dl₂ = r₂dj ₂ выразим dj ₁ = dl₁/r₁, dj ₂ = dl₂/r₂ . Подставив эти значения в уравнение с учетом того, что A₁ = t dl₂, а A₂ = t dl₁ (см. рис. 8.3) получим:

рdl₁dl₂ = s₁ tdl₂ dl₁ / r₁+s₂ t dl₁dl₂ / r₂

Разделив левую и правую части уравнения на tdl₁dl₂ получим окончательную формулу для расчета тонкостенных сосудов, которую называют формулой Лапласа:

s₁/r₁+s₂/r₂=p/t (8.6)

 

Рассмотрим расчет двух видов сосудов, наиболее часто встречающихся на практике: сферического и цилиндрического. При этом ограничимся случаями действия внутреннего газового давления.

1. Сферический сосуд. В этом случае r₁= r₂ = r, где r - радиус сферы, а s₁ =s₂= s . Из формулы (8.6) следует, что

s=рr/2t (8.7)

 

Исследования показывают, что поскольку в данном случае имеет место плоское напряженное состояние, то согласно энергетической теории провер­ка прочности ведется, как в случае одноосного напряженного состояния:

s=рr/2t£[s] (8.8)

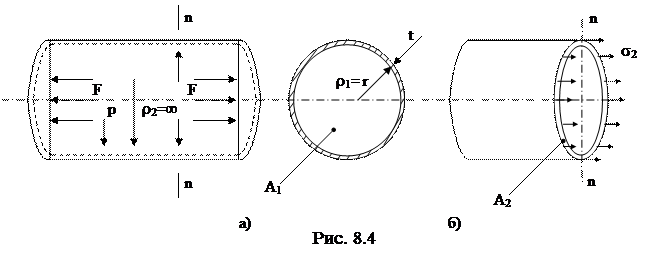
2. Цилиндрический сосуд. В этом случае (рис. 8.4, а) r₁ = r - радиус ци­линдра, r₂ = ¥.

 

Из уравнения Лапласа получаем s₁/r=p/t, откуда

s₁=pr/t (8.9)

Для определения напряжения s₂ используем метод сечений. Рассечем со­суд плоскостью п-п, перпендикулярной его оси, мысленно отбросим правую часть и рассмотрим условие равновесия левой оставшейся части (рис. 8.4, б). На неё действуют сила давления газа на днище F = рА₁ = рpr², а также внут­ренняя сила от напряжения s₂, равная N₂ =s₂А₂ =s₂2prt. Проецируя эти си­лы на ось сосуда, получаем:

-F + N₂ =0; рpr²+s₂2prt = 0, откуда s₂= pr/2t. (8.10)
Из зависимостей (8.9) и (8.10) видно, что в цилиндрическом сосуде на­пряжение в продольном сечении в 2 раза больше, чем в поперечном. Это учи­тывают на практике при изготовлении составных цилиндрических резервуа­ров: продольные сварные швы выполняют более прочными, чем поперечные.
При расчете на прочность цилиндрического сосуда рекомендуется применять
формулу, основанную на энергетической теории прочности:
s_Э= 0,86s₁ = 0,86pr/t £ [s] (8.11)

9. Напряжения в элементах конструкций при динамических нагрузках

 

9.1. Общие сведения

 

Динамическими считаются нагрузки, изменяющиеся во времени с большой скоростью. Напряжения, возникающие при колебаниях от действия динамических нагрузок, могут во много раз превосходить по своему значению напряжения от статических нагрузок. Кроме того, многие пластичные материалы при динамическом воздействии становятся хрупкими, при действии многократно повторяющейся переменной нагрузке прочность материалов резко снижается.

Общий метод расчета на динамическую нагрузку основан на известном из теоретической механики принципа Даламбера, согласно которому всякое двигающееся тело может рассматриваться как находящееся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции, равную произведению массы тела на его ускорение и направленную в сторону, противоположную ускорению.

Поэтому в случаях, когда известны силы инерции, можно применять метод сечений, а для определения внутренних нагрузок использовать уравнения статического равновесия.

В тех же случаях, когда определение сил инерции затруднено, например, при ударе, для определения динамических напряжений и деформаций используют закон сохранения энергии.

 

9.2. Напряжения при равноускоренном движении

 

Рассмотрим простейший пример. Пусть груз 1 весом С поднимается вверх с ускорением а (рис. 9.1, а). Определим напряжение в тяге 2, держащей груз, если ее площадь сечения равна А.

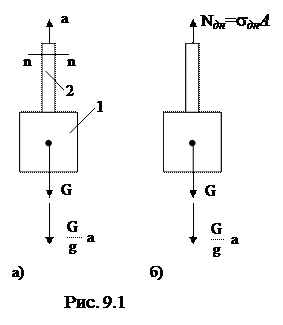
Прикладываем к грузу силу инерции та = (G/g)а и направленную вниз. Используя метод сечения, делаем мысленно разрез тяги по сечению п - п, отбрасываем верхнюю часть, обозначив внутреннее усилие в сечении N_дн (динамическое). Поскольку напряжение распределено по сечению тяги А равномерно, можно записать, что N_дн=s_днА, где s_дн - искомое динамическое напряжение в тяге.

 

 

Спроецировав все на вертикальную ось получим: s_дн А - G(1+ a/g) = 0 ,

откуда

s_дн=G/A(1+a/g) = s_ст К_дн, (9.1)
где s_ст = G/A - напряжение при статическом действии груза, К_дн =(1+ a/g)
- динамический коэффициент.

Таким образом, динамическое напряжение может быть выражено через статическое напряжение и динамический коэффициент. Это особенно удобно в тех случаях, когда динамический коэффициент приходится определять опытным путем.

9.3. Напряжения при продольном ударе

 

Пусть груз весом G падает с высоты h на неподвижный стержень (рис. 9.2, а). Под действием веса груза, а также сил инерции, которую он приобрел при падении, стержень укоротится на величину ∆l_дн (рис. 9.2, б), при этом в нем возникнет соответствующее динамическое напряжение s_дн , которое определяется с

помощью закона сохранения энергии. При этом используются следующие допущения:

1) при ударе s_дн <s_T, т.е. закон Гука сохраняет свою силу;

2) тела после удара не отскакивают друг от друга;

3) масса груза >> массы стерня;

4) пренебрегаем потерями энергии.

Приравняв работу падающего груза к потенциальной энергии деформации стержня, получаем:

∆l_дн=∆l_ст(1+)=∆l_стК_дн (9.2)
Умножив левую и правую части (9.2) на (Е/l), на основании закона Гука

получим

s_дн = s_ст К_дн (9.3)

где динамический коэффициент К_дн равен:

К _дн = 1 + (9.4)

Из этих формул видно, что динамические деформации и напряжения зависят от статической деформации ударяемого тела. Чем больше статическая деформация (при прочих равных условиях), тем меньше динамическое напряжение. Вот почему для уменьшения динамического напряжения стараются конструктивными методами увеличить статическую деформацию (например, применением амортизаторов, пружин, мягких прокладок и др.).

 

Рассмотрим два частных случая.

1. Внезапное приложение нагрузки (h= 0):

К_дн = 2, s_дн = 2s_ст , т.е. напряжения и деформации вдвое больше, чем при статическом действии того же груза.

2. Груз падает с большой высоты (h>>∆l_ст):

К_дн = (9.5)

Например, пусть ∆l_ст = 5 ·10 ^{-3 мм,} h= 250 мм, тогда согласно (9.5) К_дн = 300. Применим амортизатор, у которого при данной статической нагрузке ∆l_ст = 5мм . Получим К_дн = 10 - напряжение уменьшилось в 30 (!) раз.

 

 

10. Прочность при переменных напряжениях

 

10.1. Понятие об усталостной прочности. Основные определения

 

Многие детали авиационных механизмов в процессе работы подвергаются действию периодически изменяющихся во времени нагрузок (напряжений). Установлено, что при этом в материале деталей возникают микротрещины, которые постепенно развиваются и значительно ослабляют сечение деталей. При разрушении на поверхности излома детали наблюдаются две ярко выраженные зоны: гладкая – результат постепенного развития трещины и грубозернистая – след внезапного разрушения. Такое явление называется усталостью материала.

При переменных напряжениях разрушение детали будет проходить при напряжениях, значительно меньших предела прочности. Дополнительной характеристикой свойств материала, определяющих возможность воспринимать многократное действие переменных напряжений без разрушения, является предел выносливости. Значение предела выносливости для одного и того же материала зависит от ряда факторов, в частности от закона изменения напряжения во времени. В деталях механических систем наиболее часто напряжения изменяются по циклическому закону, близкому к синусоидальному. На рис. 10.1 показано периодическое изменение нормального напряжения во времени от наименьшего σ_min до наибольшего σ_max. Однократная смена напряжений называется циклом изменения напряжений, t_ц – время цикла.