Критерий полноты системы булевых функций (теорема

Поста)- системаполна в том и только в том случае, если для каждого рзклассов 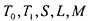в системе существует функция, не

Принадлежащая этому классу, иначе говоря, система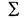полна, если рыполнены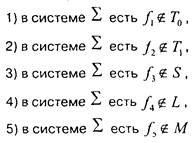5 условий

Функции 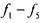- не обязательно различные

Предварительно рассмотрим 3 утверждения, которые 'демонстрируют, как суперпозициями функций системы, удовлетворяющей условию теоремы Поста, выразить функции известных полных систем Лемма 1.Суперпозициями несамодвойственной функции

и функцииможно получить функцию-константу Если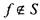, то существует набор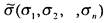такой, что

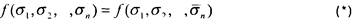
Построим суперпозицию, где вместо

|ждого переменного функции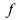подставляется либо X , либо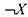Югда[ввиду (*}] =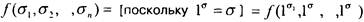

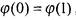Таким образома это означает, чтс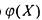- константа

Следствие.Из функции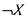и константы можно получить другую

рнстанту

Лемма 2.Суперпозициями немонотонной функции

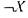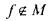и функций-констант 0 и 1 можно получить функциюЕсли , то существуют наборы и

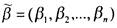такие, что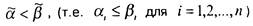и

, т.е. . Пусть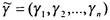- набор,

где каждое- либо переменная X , либо константа и определяется следующим образом:

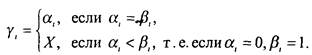
Отметим, что если X - О, то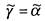; если X = 1, то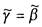. Пусть

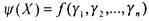. Тогда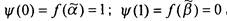, т.е.

Лемма 3.Суперпозициями нелинейной функции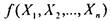функциии функций-констант 0 и 1 можно получить конъюнкцию

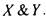
Построим для функции многочлен Жегалкина. В силу нелинейностисреди слагаемых найдется содержащее не менее 2 множителей. Пусть это переменные Тогда все слагаемые

разбиваются на 4 группы: содержащие обе переменныетолько

одну из них 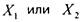и не содержащие ни одной. Объединяя

слагаемые и вынося за скобки соответствующие множители в каждой j из трехпервых групп, получим:

Функции зависят от переменных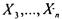, причем 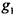не

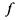равна тождественно 0, - иначе не было бы ни одного слагаемого с произведением .. Подставим в функциювместо переменных

тот набор констант, для которого_;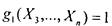

при этом функции 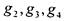обращаются в некоторые константы;

обозначим их соответственно . Получим функцию двух

переменных

Теперь произведем еще одну подстановку: в функцию подставим функцию 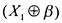вместо 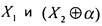вместо 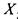. в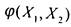

Зависимости от значений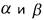каждая из этих функций представляет

собой либо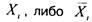, так что фактически мы подставляем либо

Переменную, либо ее отрицание. Получаем функцию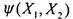, равную

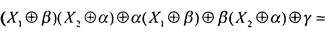[после раскрытия робок]

[после сокращений] 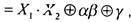т.е. сумму по модулю 2

конъюнкции и константы . Если последняя равна 0, то

построение закончено; в противном случае, т.е. если

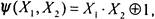
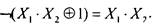то нужно подставитьв функцию:

; Теперь доказательство теоремы Поста уже достаточно просто. Необходимость следует из сделанного выше замечания: если все функции системы принадлежат какому-нибудь из 5 классов (обозначим его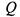), то в силу замкнутости класса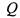все суперпозиции функций системы также принадлежат ему; в то же время в 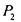есть функции, соторые не принадлежатчто означает неполноту системы.

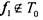
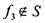
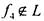
Достаточность выводится из лемм 1 -3. Пусть в системе есть функции ' 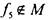(некоторые из них могут

ювпадать). Суперпозиция - функция одной

юременной, имеющая столбец значений ; аналогично,

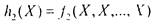- функция со столбцом значений

Возможны два случая.

- функция 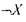. По

лемме 1, из функций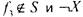можно получить константы 0 и 1.

(2)в противном случае. Тогда

По лемме 2, из функцийи констант можно получить функцию

Как видим, в обоих случаях из функций системы могут быть построены обе константы и отрицание.

По лемме 3, из функций, отрицания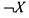и констант 0 и 1

можно получить конъюнкцию . В свою очередь, конъюнкция и

отрицание образуют полную систему, чем и завершается доказательство теоремы Поста.

Для проверки конкретной системы на полноту можно заполнить для функций системы так называемую таблицу Поста: см. табл.9, в которой исследуется система("+" означает принадлежность

функции данному предполному классу).

Принадлежность трех данных функций классам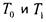проверяется

по их таблицам очень просто. Также несложно проверить принадлежность их классу М (заметим, что если и не равна 0 тождественно, то

она не монотонна). Очевидно также, что 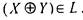, свойство

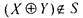следуе^т из соотношения

Функцияне самодвойственна, поскольку двойственная

/

ей, как мы знаем, другая функция - конъюнкция. Далее,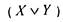

нелинейна, так как ее многочлен Жегалкина содержит

произведение . Легко проверяется также заполнение последней

строки табл.9 - для функции-константы 1. Наконец, согласно теореме Поста, для полноты системы в каждом столбце таблицы Поста должен быть хотя бы один минус.

В таблице 11 для каждого из пяти рассмотренных выше классов знаками "+" и '•'-" показана принадлежность ему ряда известных функций: всех 4 функций одной переменной, 6 функций двух переменных и 2 функций трех переменных. В отличие от предыдущей таблицы функции здесь представлены столбцами. Заметим, что в каждой Строке таблицы имеется знак "-"; другими словами, для каждого из пяти классов есть не принадлежащая ему функция и, следовательно, ни один из них не совпадает с множеством всех логических функций , а каждый является частью

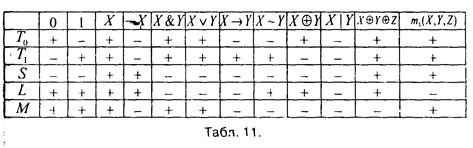
Несколько примеров полных систем рассмотрены нами в §1. Отметим интересный факт: из табл.11 можно заключить, что система, Состоящая из одной функции - штриха Шеффера 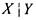- полна.

Упражнение.Проверьте, что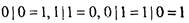Убедитесь теперь, что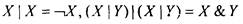

Упражнение.С помощью табл 11 установите, какиеиз цижеследующих систем является функционально полными:

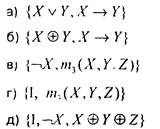
Система функций G называется независимой,если никакая функция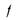этой системы не выражается через остальные, т е.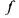не принадлежит замыканию системыНезависимая система

функций G называется базисом замкнутого классаК , если всякая функция 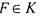есть суперпозиция функций из G . Можно определить

понятие базиса и так базис замкнутого классаК - система функций, замыкание которой равно К , причем любое подмножество К (кроме самого К ) уже не обладает этим свойством.

Примеры: 1) Система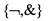- независимая.

Упражнение.Убедиться в этом, используя соотношенияи замкнутость классов L и Т .

2) Системане является независимой, поскольку, как мы знаем,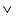можно выразить через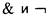или, наоборот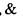-черези

3) Система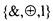- независима, в чем можно убедиться, построив для нее фрагмент таблицы Поста (табл.10). Действительно, для каждой из трех функций в этой таблице имеется класс, которому она не принадлежит, но принадлежат две остальные и, следовательно, все их суперпозиции

В примерах 1-3 представлены полные системы функций. Теперь рассмотрим пример независимой системы для замкнутого класса, не

совпадающего с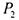

Система 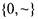не полная, так как обе функции линейны, и

представляет базис класса L Действительно,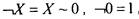

а каждая линейная функция

выражается через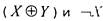Независимость функций системы

также легко проверить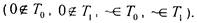

Некоторые следствия теоремы Поста.

Следствие 1. Всякий замкнутый класссодержится целиком

хотя бы в одном из 5 предполных классов 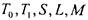иначе он

представлял бы полную систему и, в силу замкнутости, равнялся бы

Следствие 2объясняет название предполныхклассов еслик какому-нибудь из них, допустим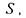(для других классов рассмотрение аналогичное) добавить любую не принадлежащую ему функциюто Замыкание системы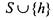совпадает с 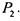Действительно, система

шире, чем S и, в то же время, не может входить в какой-либо из остальных 4 классов, так как тогда в нем содержался бы целиком класс S , что противоречит замечанию в конце предыдущего параграфа

Иначе говоря, между предполным классом и 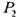не может существовать промежуточный замкнутый класс. Отсюда -

Следствие 3.В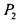существуют лишь 5 предполных классов, т е. обладающих свойством, сформулированным в следствии 2 Это рассмотренные • - 'и

Следствие 4.Из лемм 1-3 и доказательства теоремы можно заключить, что если в системе функций присутствуют константы 0 и 1, то для ее полноты достаточно, чтобы в ней содержались немонотонная функция и нелинейная функция.