Множества и элементарные операции над множествами
Математический анализ
Мы будем использовать следующие символы математической логики:
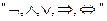для обозначения соответственно отрицания «не» и связок «и», «или» (здесь союз «или» не разделительный), «следует» и «равносильно».
Символ 
будет обозначать у нас «равно по определению».
Мы будем также использовать логические символы: квантор общности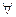 
(вместо слов «любой», «всякий») и квантор существования 
(вместо слов «существует», «найдется»). Знаком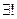 
будем заменять выражение «существует и единственно», а двоеточием «:» слова «такое, что».
Множества и элементарные операции над множествами
Под множествами понимаются собрания элементов любой природы. Множество, не содержащее элементов, называют пустым множеством и обозначают символом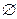 
. Тот факт, что элемент 
принадлежит множеству 
записывается как 
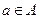, если не принадлежит, то пишут 
.
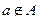Если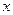 
- элемент множества, а 
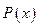- обозначение того, что он обладает свойством 
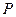, то через 
, будем обозначать все элементы, обладающие свойством .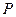
Множества называются равными 
, если они состоят из одних и тех же элементов, если все элементы множества содержатся в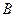 
, то пишут 
:
.
Тогда
.
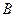Пусть и - подмножества множества 
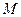. Определим простейшие операции над множествами: объединение - 
(множество, состоящее из всех элементов, содержащихся в или в ):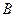
;
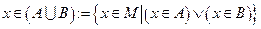пересечение - 
(множество, состоящее из всех элементов, содержащихся как в , так и в ):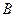
;
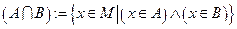разность между множествами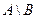 
(множество, состоящее из всех элементов, которые принадлежат , но не принадлежат ):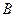
.
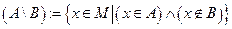Разность между множеством 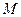и его подмножеством называют дополнением в 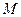и обозначают 
или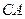 
, когда ясно, в каком множестве ищется дополнение.
Прямое (декартово) произведение множеств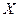 
и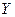 
- это множество упорядоченных пар 
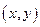таких, что 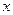принадлежит 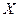, а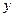 
- :
.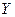