КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
Л Е К Ц И Я 12
КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
В квантовой механике уравнение Шредингера для сколько-нибудь реалистических систем невозможно решить точно, в квадратурах. Поэтому здесь создано большое количество приближенных методов исследования. Мощнейший из них - теорию возмущений - мы рассмотрим позже. А сейчас обсудим квазиклассическое приближение, которое представляет и самостоятельный интерес, так как устанавливает связь квантовой механики и классической. Как мы увидим, квазиклассическое приближение (ККП) справедливо в случаях, когда де-бройлевские длины волн частиц малы по сравнению с характерными масштабами системы. Это аналогично тому, что волновая оптика в пределе малых длин волн переходит в геометрическую.
Рассматриваем стационарное одночастичное уравнение Шредингера в координатном представлении:
 Ñ2y (r) +V(r) y(r) = Ey(r)
Ñ2y (r) +V(r) y(r) = Ey(r)
и делаем в нем формальную подстановку (замену функции)
y(r) = A .
.
Учитывая, что
Ñy = 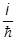 (ÑS)A
(ÑS)A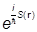 , Ñ2y =
, Ñ2y = 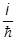 (Ñ2S)A
(Ñ2S)A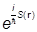 -
- 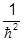 (ÑS)2A
(ÑS)2A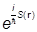 ,
,
получим для S следующее уравнение:
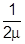 (ÑS)2 -
(ÑS)2 -  Ñ2S +V - E = 0.
Ñ2S +V - E = 0.
Если отбросить второй член, то получим
 (ÑS)2 +V = E.
(ÑS)2 +V = E.
Но это есть не что иное, как классическое уравнение Гамильтона - Якоби для функции действия S0 (укороченное). Приближение справедливо при
|ÑS|2 >>  |Ñ2S|.
|Ñ2S|.
Но в классике ÑS=p, а потому
½p2½>> ½divp(x)½,
½divp(x)½,
или, в одномерном случае
p2 >>  |
|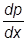 | Þ 1 >>
| Þ 1 >> 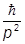 |
|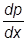 | = |
| = | | = |
| = |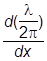 | º |
| º | |,
|,
где 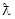 - де-бройлевская длина волны. Таким образом, переход возможен при условии
- де-бройлевская длина волны. Таким образом, переход возможен при условии
|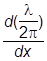 | << 1,
| << 1,
т.е. когда длина волны де Бройля мало меняется на протяжении системы. Можно сказать и иначе. Учитывая, что
p(x) =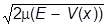 ,
,
получим
1 >> |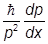 | = |
| = |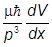 | Þ |
| Þ | | << 1.
| << 1.
Приближение справедливо, когда сила невелика (потенциальная энергия достаточно плавная функция координат), а импульс не слишком мал. В частности, приближение не работает вблизи точек поворота E =V(x), где p = 0, а l = µ. Это будет важно в дальнейшем.
Последующее рассмотрение проводим для одномерного движения, когда уравнение для функции S(x), входящей в волновую функцию
y(x) = A ,
,
имеет вид
i S¢ - S¢2 + 2m(E -V) = 0. (**)
S¢ - S¢2 + 2m(E -V) = 0. (**)
Решение этого точного уравнения будем искать в виде ряда по  :
:
S(x) = S0(x) + S1(x) +
S1(x) + 2S2(x) + ....
2S2(x) + ....
Этот ряд сходится плохо, и отыскание поправок высшего порядка малости по  затруднено. К тому же разложение разумно (т.е. может получать эффективные результаты) только при обсужденном выше условии. Ограничимся поправками, линейными по
затруднено. К тому же разложение разумно (т.е. может получать эффективные результаты) только при обсужденном выше условии. Ограничимся поправками, линейными по  , т.е. ищем S в виде
, т.е. ищем S в виде
S(x) @ S0(x) +  S1(x) .
S1(x) .
Подставляем в (**), отбрасывая члены с  2:
2:
2m(E -V) - S0¢2 + (iS0¢¢ - 2S0¢S¢1) = 0.
(iS0¢¢ - 2S0¢S¢1) = 0.
Это должно быть тождеством, а потому должны равняться нулю отдельно члены без  (с
(с  0) и члены с
0) и члены с  (
( 1):
1):
2m(E -V) - S0¢2 = 0, iS0¢¢ - 2S0¢S1¢ = 0.
Собственно говоря, именно это приближение и называется квазиклассическим. Оно же именуется методом ВКБ (Вентцеля - Крамерса - Бриллюэна).
Уравнение нулевого приближения есть уравнение Гамильтона - Якоби, из которого
S0¢ = ± 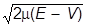 = ±p,
= ±p,
где
p(x) =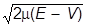
классический импульс.
Итак, в нулевом приближении
S0(x) = ±  |p(x)|dx.
|p(x)|dx.
|
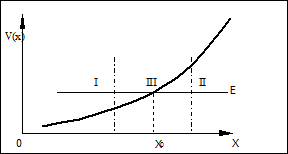
Здесь x0 - координата некоторой фиксированной точки на прямой. В качестве нее удобно выбирать классическую точку поворота, где
E =V(x0).
Заметим, что в классически доступной области I импульс вещественен, а в классически недоступной области II он является чисто мнимым.
Уравнение для S1 переписываем в виде
S1¢ = i/2(S0’’/S0’) º i/2(lgSo’)’.
Интегрируя его, находим
S1 = i/2lgS’0 = i/2(lgp)
(постоянная интегрирования несущественна, и ее опускаем). Таким образом, в приближении ВКБ
S(x) = ±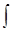 pdx+i
pdx+i ln
ln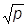 ,
,
и
y(x) = 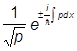 .
.
Обращаясь к картинке, запишем этот результат отдельно в областях I (x<x0, классически доступная) где импульс вещественен, и II (x>x0, классически недоступная), где импульс мнимый:
I.yI(x) =  , p(y) =
, p(y) = 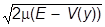 ,
,
или
yI(x) =  [a sin (z +g) +bcos(z +g¢)], z(x) º
[a sin (z +g) +bcos(z +g¢)], z(x) º  |p(y)dy|;
|p(y)dy|;
II. yII(x) = 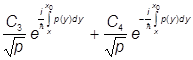 , p(y) =
, p(y) =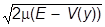 = ip(y),
= ip(y),
или
yII(x) = 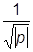 [Ae-|z|+Be|z|], |p(y)| =
[Ae-|z|+Be|z|], |p(y)| = , |z| º
, |z| º  |p(y)|dy.
|p(y)|dy.
В эти решения входят 6 неизвестных вещественных констант: a, b, g, g¢, A, B. Свяжем их между собой, сшивая решения для областей I и II.
Но здесь есть значительная трудность. В точке поворота p(x0)=0, и квазиклассическое приближение здесь не работает (см. выше), т.е. выписанные функции не являются решениями задачи даже приближенно. Способ таков: вводим промежуточную область III, в которой решаем уравнение Шредингера точно, и именно это решение его концами сшиваем с соответствующими квазиклассическими решениями. Область III считаем весьма узкой, что позволяет аппроксимировать потенциал V(x) линейной функцией, разлагая его в ряд Тейлора:
V(x) @V(x0) + (x - x0)V¢(x) º E + (x-x0), a =
(x-x0), a = 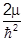 V¢(x).
V¢(x).
Тогда точное (в смысле не квазиклассическое) уравнение Шредингера в области III будет записываться как
y¢¢(x) - a (x-x0) y(x) = 0.
После замены переменной
h = a1/3(x-x0)
оно примет вид
 - hy = 0.
- hy = 0.
Это есть уравнение Эйри, и оно имеет два независимых решения:
u1(h) =  , u2(h) =
, u2(h) = 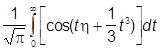 .
.
Теперь будем сшивать решения по границам областей I - III и III - II.
1. При x>x0 за счет  2 в знаменателе a имеем h>>1, и для функций Эйри можно воспользоваться известными из справочников асимптотическими выражениями (кстати, они получаются методом перевала):
2 в знаменателе a имеем h>>1, и для функций Эйри можно воспользоваться известными из справочников асимптотическими выражениями (кстати, они получаются методом перевала):
u1 » 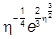 , u2 =
, u2 =  .
.
2. При x<x0 по тем же причинам h<<-1, и асимптотики таковы:
u1 »  , u2 »
, u2 » 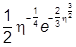 .
.
Первую асимптотику будем сшивать с yII(x), а вторую - с yI(x).
(а) В области I x=x0 -e (e>0, e ® 0) подставляем в p(x) потенциал
V(x) =  (x0-x)
(x0-x)
разлагаем в ряд Тейлора и вычисляем
z = 
 p(y)dy @ 2/3 h3/2.
p(y)dy @ 2/3 h3/2.
(б) В области II x=x0+e, и аналогичные выкладки дают
|z| @ 2/3 h3/2.
Теперь, задавшись решением в I, сшиваем его с асимптотикой (2), находим асимптотику того же решения в (1) и сшиваем с решением II. Решая возникающие алгебраические уравнения, получим
A = a/2, B = b, g = g¢ = 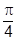 .
.
В итоге получим следующее квазиклассическое решение:
y(x) = ay1(x) + by2(x),
где
y1(x) =  ; y2(x) =
; y2(x) = 
При этом константы a и b находятся из общих граничных условий (скажем, ограниченность на бесконечности) и условий нормировки. Полученные решения справедливы, вообще говоря, только вне e- окрестности точки поворота. Но если на интервале 2e укладывается много длин волн де Бройля, то выражениями можно пользоваться во всей области.