Первообразная функция и неопределенный интеграл
ТЕМА «НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
ЛЕКЦИЯ № 1
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ПЛАН
1. Первообразная функция и неопределенный интеграл.
2. Свойства неопределенных интегралов.
3. Таблица основных неопределенных интегралов.
Первообразная функция и неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу – нахождение самой функции по….
Доказательство. Так как F(x) и Ф(х) первообразные для f(х), то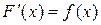 
и 
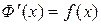. Поэтому 
. А это означает, что 
, где С – постоянное число. Следовательно,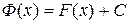 
.
Определение. Совокупность всех первообразных для функции f(х) на проме- жутке Х называется неопределенным интегралом от функции f(х) на этом промежутке и обозначается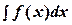 
, где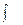 
- знак
интеграла, f(х) - подынтегральная функция, f(x)d x – подынте-
гральное выражение.
Таким образом,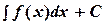 
, (1)
где 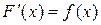, С – произвольная постоянная.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
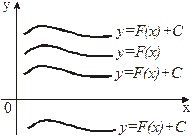
Назовем график первообразной от f(х) инте-
гральной кривой. Таким образом, если
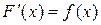, то график функции у = F(x) есть
интегральная кривая. Неопределенный интеграл
геометрически представляет семейство всех ин-
тегральных кривых. Все кривые из этого семей-
Рисунок 1 ства у = F(x) + С могут быть получены из
одной интегральной кривой параллельным
сдвигом в направлении оси Оу.
Теорема. Всякая непрерывная на множестве Х функция f(х) имеет на этом
множестве первообразную, а следовательно, и неопределенный
интеграл.
Свойства неопределенных интегралов
Производная от неопределенного интеграла равна подынтегральной функции, т.е. .
Доказательство. Дифференцируя левую и правую часть равенства (1), получаем: .
Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. .
Доказательство. По определению дифференциала и свойству 1 имеем: 
.
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .
Доказательство. По определению дифференциала и рассматривая функцию F(x) как первообразную для некоторой функции f(х) имеем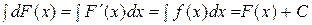 
.
Постоянный множитель можно выносить за знак интеграла, т.е. .
Доказательство. 
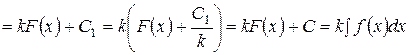(положили 
).
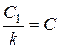Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций, т.е. .
Доказательство. Пусть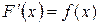 
и 
. Тогда 
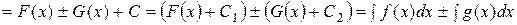, где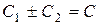 
.
Инвариантность формулы интегрирования). Если , то и , где - произвольная функция, имеющая непрерывную производную.
Доказательство. Пусть х - независимая переменная, f(х) – непрерывная функция и F(x) – ее первообразная. Тогда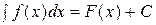 
. Положим 
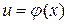, где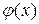 
- непрерывно-дифференцируемая функция. Рассмотрим сложную функцию 
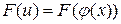. В силу инвариантности формы дифференциала первого порядка функции имеем 
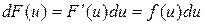. Отсюда 
.
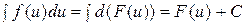Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Таблица основных неопределенных интегралов
Интегралы в приводимой ниже таблице называются табличными.
В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций. Методы нахождения первообразных сводятся к указанию приемов, приводящих данный интеграл к табличному. Поэтому, необходимо знать табличные интегралы и уметь их узнавать.
В таблице основных интегралов переменная интегрирования U может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
Таблица интегралов