Несобственные интегралы первого рода по неограниченному промежутку
ТЕМА «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
ЛЕКЦИЯ № 9
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ПЛАН
1. Несобственные интегралы первого рода по неограниченному промежутку.
2. Несобственные интегралы второго рода от неограниченной функции.
3. Свойства несобственных интегралов.
Рассматривая определение определенного интеграла, как предела интегральных сумм, мы предполагали, что функция f(х) задана на отрезке 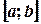 и непрерывна на нем.
и непрерывна на нем.
Если же область интегрирования бесконечна, например, задана интервалом 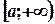 , то даже для непрерывной функции f(х) обычное определение интеграла становится неприемлемым, так как при любом разбиении интервала
, то даже для непрерывной функции f(х) обычное определение интеграла становится неприемлемым, так как при любом разбиении интервала 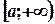 на конечное число частей одна из них будет бесконечной.
на конечное число частей одна из них будет бесконечной.
В случае разрыва функции в какой-либо точке отрезка 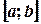 определение определенного интеграла так же непригодно. Поэтому необходимо обобщить понятие определенного интеграла на случай бесконечной области интегрирования или разрывной подынтегральной функции.
определение определенного интеграла так же непригодно. Поэтому необходимо обобщить понятие определенного интеграла на случай бесконечной области интегрирования или разрывной подынтегральной функции.
Несобственные интегралы с бесконечными пределами
Пусть функция f(х) непрерывна на промежутке . Тогда для любого отрезка… Определение. Если существует конечный предел , то его назы-Геометрический смысл несобственного интеграла
Свойства несобственных интегралов
Сформулируем два общих свойства для несобственных интегралов I и II рода, применяемых при решении задач.
Признак сравнения.
Замечание: в этом свойстве пределы интегрирования могут быть бесконечными (для несобственных интегралов I рода), или функции разрывными (для…Эталонные интегралы.
При исследовании сходимости интегралов с помощью признаков сравнения данные интегралы сравниваются с эталонными интегралами, о которых известно, сходятся они или расходятся. К эталонным обычно относят следующие интегралы:
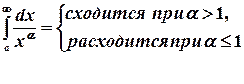 ;
; 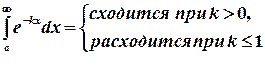 ;
;
 .
.