Моделирование и проектирование в инфокоммуникационных технологиях

 

 

И.А.Оболонин

 

Моделирование и проектирование в инфокоммуникационных технологиях

2013 г. УДК 621.38:004  

Введение

 

С развитием системных исследований, с расширением экспериментальных методов изучение реальных явлений все большее значение приобретают абстрактные методы, появляются новые научные дисциплины, автоматизируются элементы умственного труда.

Важное значение при проектировании реальных систем имеют математические методы анализа и синтеза. Однако было бы неправильно забывать о том, что основным критерием любой теории является практика, и даже сугубо математические, отвлеченные науки базируются в своей основе на фундаменте практических знаний. Одновременно с развитием теоретических методов анализа и синтеза совершенствуются и методы экспериментального изучения реальных объектов, появляются новые средства исследования. Эксперимент был и остается одним из основных инструментов познания. Подобие и моделирование позволяют по-новому описать реальный процесс и упростить экспериментальное его изучение.

Известно, что сложные системы, к которым относятся системы телекоммуникаций и мультимедиа, могут быть разбиты на следующие типы: технические, экономические, биокибернетические и социальные [Ивченко Б.П., МартыщенкоЛ.А., Монастырский М.Л. Теоретические основы информационно-статистического анализа сложных систем. – СПб.: Лань, 1997. – 320 с.].

Авторы данного учебника не ставили перед собой задачу ознакомить читателей с методами проектирования, а, следовательно, и моделирования (т.к. эти процессы неразрывны) всех вышеперечисленных типов сложных систем. Целью данного учебника является ознакомить читателя с мировоззренческими и практическими аспектами теории моделирования.

Структуры современных технических систем отличаются большим разнообразием и сложностью. В связи с этим перед разработчиками систем возникает ряд серьезных проблем, связанных, в частности, с проведением на начальных стадиях проектирования качественного и количественного анализа эффективности функционирования систем.

Немаловажную роль при этом играют средства контроля работоспособности и поиска неисправности, которые основываются на методах моделирования сложных систем и их диагностирования.

Глава 1. ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ, КЛАССИФИКАЦИЯ

 

Понятия системы, модели и моделирования

Одним из основных понятий является система – это целостность, иерархически организованная множеством функций и соответствующих им управленческих… Далее следует рассмотреть понятие модели и моделирования. Модель – способ замещения реального объекта, используемый для его изучения.

Классификация радиотехнических устройств

 

Иерархия построения радиотехнической системы может быть пред­ставлена в виде своеобразной пирамиды (рис. 1.2).

 

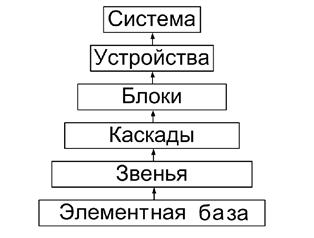
Рис. 1.2 Иерархия радиотехнической системы

 

Нижний уровень «пирамиды» составляет элементная база (транзисторы, диоды, конденсаторы, микросхемы и десятки иных наименований). Из них составляются звенья (например, LC-контур), объединяемые в функционально законченные цепи-каскады (усилители, автогенераторы, модуляторы и т.п.).

Следующий уровень – блоки, например, блок усиления мощности ВЧ колебаний, блок обработки сигнала, линейный тракт радиоприемника и т.д.

Еще более высокий этаж «пирамиды» включает функционально за­конченные устройства – радиоприемники, радиопередатчики, радиостанции, радиолокаторы и т.д., которые работают самостоятельно в составе различных радиотехнических систем (например, система радиосвязи, радиовещания, радиолокации).

В случае применения в устройствах только интегральных микросхем три нижние уровня объединяются в один.

Физические процессы, связанные с преобразованием сигналов, про­текают на всех уровнях «пирамиды». Исследование процессов можно проводить в частотной и временной областях.

Каскады и звенья, применяемые в радиотехнических устройствах, вне зависимости от их назначения, можно классифицировать по четырем основным признакам:

1. Влияния амплитуды, сигнала на их параметры и характеристики, что приводит к делению всех объектов на линейные и нелинейные;

2. Отсутствие или наличие в них электронных приборов, что делит их на пассивные и активные;

3. Взаимодействия с внешними сигналами – автономного или неавто­номного типа;

4. Диапазоны частот и используемые в этой связи элементы – с сосредоточенными или распределенными постоянными.

Отличительные признаки устройств согласно данной классификации

 

Линейные и нелинейные устройства –определяющий признак деления – это зависимость их параметров ихарактеристик от амплитуды сигнала.

В линейных устрой­ствах такая зависимость отсутствует, в нелинейных – имеет место.

Нелинейным звеном в большинстве случаев является электронный прибор. В линейных устройствах, как правило, амплитуда сигнала относительно невелика – режим «малого» сигнала.

Напротив, в нелинейных устройствах, как правило, амплитуда сигнала сравнительно велика и имеет место режим «большого» сигнала.

Работа линейных устройств описывается одним или системой линейных дифференциальных уравнений, а нелинейных – нелинейными дифференциальными уравнениями.

 

Устройства пассивного и активного типа

 

Отличительным признаком активного устройства является преобразование в нем энергии из одного вида в другой. В состав активных устройств обязательно входят электронные приборы.

(В состав пассивных устройств входят: резисторы, конденсаторы, индуктивности, резонаторы и т.д.).

Устройства автономного и неавтономного типа

 

Признаки устройств неавтономного типа:

1) Зависимость выходного сигнала от входного;

2) Изменение параметров входного сигнала при его прохождении через устройство (в усилителях повышается мощность сигнала, в преобразователях изменяется частота).

Признаком устройств автономного типа является отсутствие внешнего воздействия (в них выходной сигнал определяется только свойствами самого устройства) – пример автогенератор.

 

Устройство с элементами сосредоточенного и распределенного типа

 

Элементы с распределенными постоянными – это волноводы и объемные резонаторы, отрезки фидерных (коаксиальных, полосковых и микрополосковых) линий.

Анализ устройств с элементами сосредоточенного типа базируется на обыкновенных дифференциальных уравнениях, а с распределенными постоянными – на дифференциальных уравнениях с частными производными.

 

Основные типы задач в радиотехнике

Несмотря на большое разнообразие задач, решаемых в рамках дисциплин, объединяемых понятием «радиотехника», формально их можно свести к пяти основным… · моделированию; · расчету;

Развитие понятия модели

Моделирование – форма человеческой деятельности, в основе которой лежит построение, использование и совершенствование моделей. Первоначально моделью… · манекен – модель человека; · уменьшенные копии судов и самолетов в качестве прототипов;

Модель как философская категория

Осмысливание основных особенностей моделей привело к разработке многочисленных вариаций определений типа: модель – некий объект-заменитель, воспроизводящий интересующие нас свойства и… Затем были осознаны модельные свойства чертежей, рисунков, карт –реальных объектов искусственного происхождения,…

Познавательные и прагматические модели

Все виды деятельности удобно разделить по направленности потоков информации, циркулирую­щих между субъектом и окружающим миром. С этой точки зрения… · Познавательные модели являются формой организации и представления знаний,… · Прагматические модели являются средством управления, средством организации практических действий, способом…

Пример.

Прагматические модели: планы, устав организаций, кодексы законов, экзаменационные билеты и др. Познавательные модели: теория электрических цепей, теория электромагнитного поля, теория сигналов и др. Не следует абсолютизировать приведенную классификацию. Например, детская игрушка или карта местности имеют признаки обеих моделей.

 

 

Статические и динамические модели

Другим принципом классификации целей моделирования может служить разделение моделей на статические и динамические. Для одних целей может…  

Способы воплощения моделей

 

Рассмотрим теперь, какими средствами выражаются отношения между отображаемым и отображающим объектами и из какого «материала» строятся модели.

 

Абстрактные модели и роль языков

Абстрактные модели являются идеальными конструкциями, построенными средствами мышления, сознания. Прежде всего, обсудим абстрактные модели,… Естественный язык – универсальное средство построения любых абстрактных… Дифференциация наук объективно потребовала создания специализированных языков, более четких и точных, чем…

Материальные модели и виды подобия

Чтобы некоторая материальная конструкция могла быть отображением, т.е. замещала в каком-то отношении оригинал, между оригиналом и моделью должно… Прямое подобие – фотография, макет здания, выкройка одежды, и т.д. Следует… Косвенное подобие между оригиналом и моделью устанавливается не в результате их физического взаимодействия, а на…

Условия реализации свойств моделей

 

Для того чтобы модель отвечала своему назначению, необходимо обеспечить соответствующие условия для ее функционирования. Их отсутствие лишает модель ее модельных свойств.

 

Пример.

1) Бумажные деньги могут играть роль модели стоимости пока в среде их обращения существуют правовые нормы и финансовые учреждения, поддерживающие их функционирование. Царские ассигнации и «керенки» может быть и имеют историческую ценность, но уже не как деньги.

2) Программа для ЭВМ дает результат только при определенных условиях и малейшее рассогласование в ней с языком машины полностью обесценивает программу.

Вывод: для реализации свойств модельных функций необходимо, чтобы модель была согласована со средой, в которой ей предстоит функционировать, входила в эту среду не как чуждый ей элемент, а как ее естественная часть.

 

Соответствие между моделью и действительностью в аспекте различия

 

Конечность моделей

Мир, частью которого мы являемся, бесконечен, как бесконечен и любой объект, не только в пространстве и времени, но и в своих связях с другими… · ограниченность числа нервных клеток; · ограниченность числа действий, которые мы можем выполнить в единицу времени;

Упрощенность моделей

Рассмотрим, как с помощью конечных моделей отображается весьма эффективно бесконечная действительность. Прежде всего, отметим, что сама конечность… Следующая причина вынужденного упрощения модели связана с необходимостью… Есть еще один, довольно загадочный аспект упрощенности моделей. Почему-то оказывается, что из двух моделей, одинаково…

Приближенность моделей

Второй фактор, позволяющий преодолевать бесконечность мира в конечном познании – это приближенность (приблизительность) отображения действительности… Приближенность модели может быть очень высокой, например, голографические…  

Адекватность моделей

Модель, с помощью которой успешно достигается поставленная цель, будем называть адекватной поставленной цели. Заметим, что адекватность не полностью… В ряде случаев удается ввести некоторую меру адекватности модели – т.е.…  

Соответствие между моделью и действительностью в аспекте сходство

Вопрос о сходстве между моделью и оригиналом более трудный по сравнению с проблемой различий. Поскольку различия между моделью и реальностью…  

Истинность моделей

Степень правильности относительных истин обычно проверяется практикой. Однако следует подчеркнуть, что об истинности, правильности или ложности…  

О сочетании истинного и ложного в модели

Еще один важный аспект «истина-ложь» модели состоит в том, что ошибки в предположениях имеют разные последствия для прагматических и познавательных…  

Сложности алгоритмизации моделирования

Огромный опыт работы с моделями показывает, что не существует универсального, пригодного для всех случаев жизни алгоритма работы с моделями. Это… 1) Каждая модель функционирует в определенной среде. Конкретное окружение… 2) Требования, предъявляемые к модели противоречивы: полнота модели противоречит ее простоте, точность модели – ее…

Основные типы моделей

Понятие проблемной ситуации при создании системы

Цели, которые ставит исследователь, редко достижимы только за счет его собственных возможностей или внешних средств, доступных в данный момент.… В результате, требуется предпринять некоторые действия, направленные на отбор…  

Основные типы формальных моделей

Модель «черного ящика». Приведенное выше определение ничего не говорит о внутреннем устройстве системы. Поэтому ее можно изобразить в виде… Рис. 1.5 Модель «черного ящика»

Взаимосвязи моделирования и проектирования

Моделирование теснейшим образом связано с проектированием. Обычно сначала проектируют систему, потом её испытывают, потом снова корректируют проект… Если требуется уточнение, эти этапы повторяются вновь и вновь: формализация… Проектирование – процесс создания объекта и его модели; моделирование – способ оценки результата проектирования;…

Точность моделирования

Поскольку моделирование – способ замещения реального объекта его аналогом, то возникает вопрос: насколько аналог должен соответствовать исходному… Вариант 1: соответствие – 100%. Очевидно, что точность решения в этом случае… Вариант 2: соответствие – 0%. Модель совсем не похожа на реальный объект. Очевидно, что точность решения минимальна, а…

Глава 2. КЛАССИФИКАЦИЯ МЕТОДОВ МОДЕЛИРОВАНИЯ

 

Методы моделирования можно классифицировать в соответствии со следующими критериями:

1. По характеру изучаемых процессов:

· детерминированное – предполагается отсутствие всяких случайных воздействий и, как следствие, возможны точные решения;

· стохастическое – учитываются случайные факторы, влияющие на работу моделируемой системы (вероятностные оценки).

2. По признаку развития процессов во времени:

· статическое – описание моделируемой системы в какой-либо конкретный момент;

· динамическое – отражает поведение объекта во времени.

3. По представлению информации в модели:

· дискретное, непрерывное, дискретно-непрерывное.

С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные). Под аналоговой моделью понимается модель, которая описывается уравнениями, связывающими непрерывные величины. Под цифровой понимают модель, которая описывается уравнениями, связывающими дискретные величины, а под аналого-цифровой – модель, связывающая аналоговые и цифровые величины.

4. В зависимости от формы представления объекта моделирования можно выделить реальное и мысленное.

Реальное – объект есть или его можно создать.

Мысленное – если объект моделирования не существует, либо существует вне условий для его физического создания.

Реальное моделирование

При реальном моделировании используется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части.… а) натурное моделирование (можно поставить эксперимент на объекте, либо на его… б) физическое моделирование (на специальных установках, имеющих физическое подобие).

Мысленное моделирование

Если объект моделирования не существует, либо существует вне условий для его физического создания.   наглядное

Глава 3. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

 

Для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т.е. построена математическая модель.

Под математическим моделированием следует понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. Исследование этой модели, позволяет получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.

Любая математическая модель описывает реальный объект лишь с некоторой степенью приближения к действительности, математическое моделирование можно разделить на аналитическое, имитационное и комбинированное.

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегральных, дифференциальных, конечно-разностных и т.п.) или логических условий.

Аналитическая модель может быть исследована следующими методами:

а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик;

б) численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных;

в) качественным, когда не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными. Однако такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности, которые часто бывают непреодолимыми. Поэтому, желая использовать аналитический метод, в этом случае идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Такое исследование на упрощенной модели аналитическим методом помогает получить ориентировочные результаты для определения более точных оценок другими методами.

Численный метод позволяет исследовать по сравнению с аналитическим методом более широкий класс систем, но при этом полученные решения носят частный характер.

Численный метод особенно эффективен при использовании компьютеров.

В отдельных случаях исследования системы могут удовлетворить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Такие качественные методы широко используются, например, в теории математического управления для оценки эффективности различных вариантов систем управления.

При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени. Имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Это позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы.

Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач.

Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод получения информации о поведении системы, особенно на этапе ее проектирования.

Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели.

Математическая модель системы – это совокупность соотношений (формул, неравенств, уравнений, логических соотношений), определяющих характеристики состояний в зависимости от ее внутренних параметров – начальных условий, входных сигналов, случайных факторов и времени.

Пример: Возьмем некоторую простую систему регулирования, структурная схема которой представлена на рис. 3.1.

Рис. 3.1 Система регулирования

 

Математической моделью системы является дифференциальной уравнение

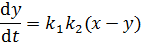
или

 

Характеристики состояния системы

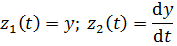
Функционирование системы заключается в изменении характеристик состояния во времени. В некоторых случаях характеристики состояния могут определяться в виде явных функций от параметров системы, входных сигналов, начальных условий и времени. В других случаях модель представляет собой систему уравнений относительно характеристик состоянии системы и выходных сигналов. При этом параметры входят в коэффициенты уравнений, а входные сигналы – в их правые части.

Вид математической модели определяется природой реального объекта, и теми задачами, для решения которых строится модель, а также требуемой точностью их решений. Поэтому необходимо исследование полученной модели с целью определения области ее наиболее эффективного использования при решении инженерной задачи и установления границ изменения переменных, в которых она справедлива.

Рассмотрим в качестве примера построение модели Солнечной системы.

Наблюдение за звездным небом начались еще в глубокой древности. Первичный анализ этих наблюдений позволил выделить планеты из всего разнообразия небесных светил. Следовательно, первым шагом было выявление объекта исследования. Другим шагом стало выявление закономерности движения планет, то есть «аксиом» гипотетической модели. Сначала была создана модель Птолемея (II ст. до н.э.) – геоцентрическая модель. В ней Солнце и планеты двигались вокруг Земли. Эти движения описывались с помощью правил (формул), но по мере накопления результатов наблюдения они постоянно усложнялись.

М.Коперник в 1543 году предложил принципиально новую модель Солнечной системы – гелиоцентрическую. В ней все планеты вращаются вокруг Солнца.

Однако эта модель еще не было математической, поскольку не было параметров модели (скоростей движения планет, параметров орбит и т.д.).

В XVII в. Кеплер сформулировал законы движения планет. Они описывали кинематику движения каждой планеты в отдельности, не касаясь причин, вызывающих это движение.

И.Ньютон во 2-й половине XVII века предложил динамическую модель Солнечной системы. Она базировалась на открытом им законе всемирного тяготения. Динамическая модель Ньютона согласовалась с кинематической моделью Кеплера.

Однако в 40-х годах XIX ст. результаты динамической модели стали противоречить накопленным результатам наблюдений. Например, движение планеты Уран отклонялось от теоретически вычисленного движения на модели. Это позволило Леверье в 1846 г. предсказать новую планету – Нептун, которая влияет на движение планеты Уран. Позже в том месте, на которое указал Леверье, действительно была открыта планета Нептун.

Подобным образом была предсказана и позже открыта в 1930 г. планета Плутон. Одновременно в открытием новых планет, совершенствовалась и модель Солнечной системы.

 

Этапы создания математических моделей

В общем случае под математической моделью объекта (системы) понимается любое математическое описание, отражающее с требуемой точностью поведения… Математическая модель системы – это совокупность соотношений (формул,… Процесс создания математической модели можно разбить на этапы отраженные на рис. 3.2.

З.2 Компонентные и топологические уравнения моделируемого объекта

Поведения большинства физических систем можно охарактеризовать с помощью фазовых переменных. Фазовая переменная (ФП) – это величина, характеризующая… Законы функционирования элементов системы задаются компонентными уравнениями.… Математическую модель системы получают объединением компонентных и топологических уравнений этой системы.

Компонентные и топологические уравнения электрической цепи

 

Математическая модель любой электрической цепи состоит из компонентных и топологических уравнений этой цепи.

Компонентные уравнения.

а) для линейного резистивного элемента б) для линейного индуктивного элемента

Топологические уравнения.

  (а) (б)

Глава 4. Особенности компьютерных моделей

 

Компьютерная модель обладает особыми свойствами по сравнению с математической моделью. Она не является просто записанной на другом языке – языке компьютера математической моделью.

Компьютерная модель имеет две составляющие – программную и аппаратную (рис. 4.1).

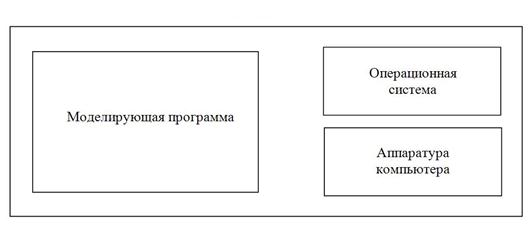
Рис. 4.1 Компьютерная модель

 

Программная составляющая (моделирующая программа) является абстрактной знаковой моделью специального вида, которая интерпретируется физическим устройством – процессором компьютера и «выполняется». В результате мы наблюдаем некоторый физический процесс, в частности движение образов на экране, которые интерпретируем как поведение модели. Под компьютером в данном случае достаточно понимать любое устройство, состоящее из программной и аппаратной частей, способное интерпретировать и выполнять программы. Это может быть и суперкомпьютер, и встроенный микропроцессор с «зашитой» в его память программой.

Совокупность компьютера и моделирующей программы является уже физическим устройством и, таким образом, компьютерное моделирование можно считать особым видом физических моделей.

К свойствам физической модели на базе компьютеров можно отнести:

1) почти неограниченная сложность моделей;

2) разделение модели на «мягкую» часть (программное обеспечение), которую необходимо менять при переходе к другой модели, и «жесткую» часть (аппаратуру и операционную систему), которая остается неизменной.

Компьютерная модель, таким образом, в определённых условиях может выступать в качестве имитатора реального объекта. Слово «imitatio» (лат.) означает – подражание, подделка. Компьютерную модель можно «подключать» к другим реальным объектам точно так, как её физические прототипы. Это свойство компьютерных моделей позволяет использовать их в составе полунатурных моделей, собранных из реальных устройств и имитаторов реальных устройств, используемых при создании и испытании сложных технологических систем.

Следует отметить, что компьютерные модели могут создаваться не обязательно на основе математических моделей. В их основе могут лежать записанные на языке программирования представления об объекте, существующие в сознании разработчика (пунктирная линия на рис. 4.2).

Если назначение такой модели – создание на её основе математической модели и затем её реализация на вычислительной машине (сплошная линия на рис. 4.2), то такое моделирование в последнее время называют имитационным. Имитационное моделирование в этом смысле – это ещё один этап компьютерного моделирования, когда имеют дело с трудно формализуемой моделью.

 

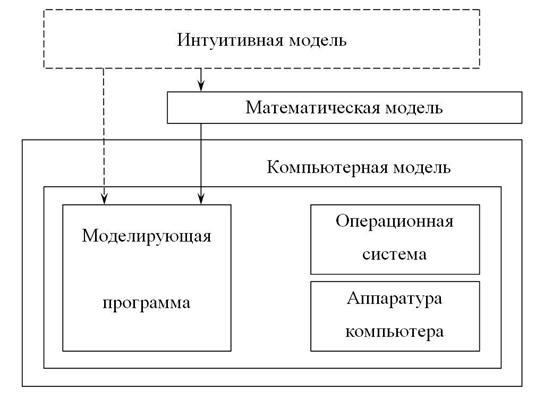
Рис. 4.2 Варианты компьютерной модели

 

Компьютерное моделирование и вычислительный эксперимент

Компьютерное моделирование всегда предполагает проведение вычислительного эксперимента. Если найти решение, например системы уравнений «ручным» методом в виде… Причем систему уравнений часто необходимо решить численно несколько раз при разном наборе параметров.

Программные средства компьютерного моделирования

На заре компьютерного моделирования все моделирующие программы были уникальными и писались непосредственно на существовавших в то время языках… В середине прошлого столетия возникла необходимость автоматизации процесса… Появление коллекций и библиотек резко расширило возможности моделирования. Если математическая модель представляла…

Системы автоматизации проектирования (САПР).

1. коллективная работа в сети; 2. экспорт – импорт файлов различных форматов; 3. масштабирование объектов;

Системы искусственного интеллекта.

Естественно-языковой интерфейс был наиболее привлекателен для общения с ЭВМ с момента ее появления. Это позволило бы исключить необходимость… Экспертные системы впервые появились в области медицины. Возникла идея… Интеллектуальные пакеты прикладных программ позволяют, аналогично экспертным системам, предварительно создавать базу…

Глава 5. ОСОБЕННОСТИ РАДИОСИСТЕМЫ КАК ОБЪЕКТА ИЗУЧЕНИЯ МЕТОДАМИ МОДЕЛИРОВАНИЯ НА ЭВМ

 

Объектами изучения методами моделирования являются радиосистемы и устройства. Радиосистемой называется совокупность технических средств, предназначенных для выполнения определенного круга задач, в которой при обмене информацией между отдельными частями системы используются радиосигналы s=s(t,λ), способные переносить информационные процессы λ = λ(t).

Классы радиосистем

Информационная сущность, являющаяся важной особенностью радиосистем определяется их функциональным назначением. С этой точки зрения радиосистемы подразделяют на следующие классы:

· системы передачи информации (СПИ) от отправителя к получателю;

· радиолокационные системы (РЛС), обеспечивающие обнаружение, сопровождение движущихся объектов и измерение их координат;

· радионавигационные системы (РНС), предназначенные для определения местоположения движущихся объектов на самих объектах;

· радиосистемы управления (РСУ) технологическими процессами и различными объектами на расстоянии;

· системы радиоразведки (СРР), обеспечивающие обнаружение радиосигналов, излучаемых различными радиосредствами, анализ и измерение их параметров и определение направления их прихода;

· системы радиопротиводействия (СРП), используемые для разрушения полезной информации в точке приема радиосигналов с целью нарушения нормального функционирования заданной радиосистемы.

Для решения практических задач отдельные радиосистемы часто приходится объединять в комплексы. Современные комплексы радиосистем обычно содержат несколько радиосистем из перечисленных выше классов. Примерами таких комплексов являются системы передачи информации через ИСЗ, автоматизированные комплексы радиосистем гидрометеослужбы и т. п. В процессе проектирования отдельных радиосистем, работаю­щих в составе комплексов, часто приходится рассматривать их во взаимодействии с другими радиосистемами. Так, например, в состав спутникового комплекса систем радиосвязи входят многоканальные СПИ, РЛС, обеспечивающие сопровождение спутников-ретрансляторов. Комплексы радиоуправления летательными аппаратами могут содержать РНС, РЛС, СПИ. Необходимо также учитывать вопросы их электромагнитной совместимости, а также наличие систем радиоразведки и радиопротиводействия.

Радиосистемы относятся к весьма специфичному классу систем. При исследовании и проектировании подобных систем методами моделирования на ЭВМ мы встречаемся с проблемой сложности, которая проявля­ется в том, что это:

· многомерные системы с очень большим числом элементов, функциональных связей между ними и статистическим характером их возникновения;

· системы, находящиеся под постоянными случайными воздействиями;

· быстродействующие системы, в которых имеют место преобразования радиосигналов одновременно со сравнительно медленно протекающими информационными процессами.

При проектировании радиосистем необходимо учитывать значительное число показателей качества.

Указанные обстоятельства приводят к тому, что без применения специальных методов упрощения математического описания моделирование радиосистем на ЭВМ оказывается практически невозможным. При этом необходимо решить следующие основные задачи, непосредственно связанные с оптимизацией процесса моделирования радиосистем на ЭВМ.

1. Разработка теории формирования математических моделей радиосистем минимальной сложности при условии обеспечения заданной точности на различных информационных уровнях их описания. При оптимизации структуры математических моделей радиосистем должны быть решены такие важные вопросы, как:

· минимизация размерности модели и упрощение связей между ее компонентами, что обусловлено выбором соответствующего способа декомпозиций радиосистемы при формировании ее модели;

· оптимизация способа дискретизации процессов в модели и методов цифрового моделирования элементов радиосистемы;

· минимизация числа реализаций процесса функционирования модели при условии получения достоверной информации о радиосистеме.

2. Развитие прогрессивных методов моделирования, позволяющих за минимальное время извлечь максимум информации об исследуемой радиосистеме. К ним, в частности, относятся методы разработки алгоритмов и сервисных программ, обеспечивающих автоматический поиск лучшего решения, оптимальных параметров радиосистемы при заданной структуре, оптимальной структуры радиосистемы по заданному критерию.

3. Создание систем автоматизированного проектиро­вания радиосистем (САПР), в которых используются методы автоматизированного математического моделирования и диалоговые режимы и процедуры.

 

Формальное описание радиосистем

Подготовка задачи к исследованию методом моделирования начинается с составления неформального (концептуального) описания радиосистемы. Неформальным описанием радиосистемы называется вся имеющаяся о ней… Описание системы, составленное по ее функциональной схеме с использованием определенного базиса операторов,…

Глава 6. ПРИМЕНЕНИЕ ПАКЕТА ПРИКЛАДНЫХ ПРОГРАММ MATHCAD ДЛЯ МОДЕЛИРОВАНИЯ ТЕЛЕКОММУНИКАЦИОННЫХ УСТРОЙСТВ

Основные сведения об универсальном математическом пакете программ MathCAD

Название системы происходит от двух слов: · MATHematica (математика) и · CAD (Computer Aided Design – системы автоматического проектирования, или САПР).

Основы языка MathCAD

Символами этого языка являются: · малые и заглавные буквы латинского и греческого алфавита; · арабские цифры от 0 до 9;

Тип входного языкаMathCAD

1. Входной язык MathCAD относится к интерпретируемому типу. Это означает, что когда система опознает какой-либо объект, она немедленно исполняет… 2. MathCAD выполняет действия над блоками в строго определенном порядке –… Это означает, что блоки нельзя располагать в документе произвольно.

Описание текстового окна MathCAD

В рабочей области текстового окна размещается вновь создаваемая программа на языке MathCAD.  

Курсор ввода

Курсор ввода устанавливается мышью. Обычно изначально он находится в левом верхнем углу окна документа. Для его установки в другое место следует подвести указатель мыши в нужное… Курсор ввода переместиться в новое место. Он намечает места ввода блоков текущего документа.

Содержание командных меню (2-ая строка)

Частично содержание меню совпадает со стандартным набором «Windows-приложений».

Поэтому дадим краткую характеристику стандартным для «Windows» меню и более подробно остановимся на содержании меню, относящихся только к MathCAD.

Идущая после заголовка составляемой или вызванной программы строка текстового окна содержит названия девяти командных меню:

Файл – Правка – Вид – Вставка – Формат – Математика – Символы –

File Edit View Insert Format Math Symbolics

– Окно – Справка

Window Help

Их вызов и раскрытие осуществляется принятым в «Windows» способом (установление курсора на соответствующем названии меню и одним щелчком левой клавиши «мыши». Закрывается меню следующим щелчком – курсор в любом месте экрана).

Меню «Файл» (File). Здесь расположены команды, связанные с исправлением текста: его полным или частичным устранением, переносом в другое место и копированием.

Меню «Вид» (View). Это меню содержит подменю, специфические для пакета «MathCAD».

В первую очередь сюда относится подменю «Панели инструментов», содержание которого представлено на рис. 6.2.

 

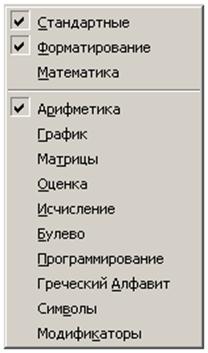
Рис. 6.2 Подменю «Панели инструментов»

 

Установив курсор в начале каждой из строк «Панели инструментов» (рис. 6.2), щелчком левой клавиши мыши можно вызвать или наоборот убрать «птичку».

Наличие последней указывает на исполнение данной команды.

Так, наличие «птички» перед строкой «Стандартные» вызывает появление 3-й строки рабочего листа, а перед строкой «Форматирование» - 5-ой строки.

Наличие «птички» перед строкой «Математика» вызывает появление панели с пиктограммами (кнопками), которым соответствуют названия, перечисленные в подменю «Математика».

 

 

Рис. 6.3 Кнопки подменю «Математика»

 

Если установить «птичку» перед каждой из строк в этом подменю, или произвести щелчок по соответствующей пиктограмме на панели «Математика», то на рабочем листе появится так называемая панель инструментов с указанием конкретных математических операций, преобразований или действий, которые могут быть выполнены с ее помощью.

Всего последовательно можно вызвать 10 панелей инструментов, перечисленных на рис. 6.3 (некоторые раскрыты на рис. 6.4).

 

 

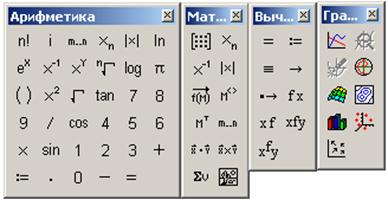
Рис. 6.4 Панели инструментов

 

Управление элементами интерфейса

· панель (стандартная) инструментов – 1; · набор палитр для ввода математических символов – 2; · панель (или линейка) форматирования – 3.

Выделение областей

   

Изменение масштаба документа

Иногда желательно изменить масштаб отображения документа. Для этого служит команда «Zoom» (масштаб) меню «View» (Вид). Она позволяет вывести окно с переключателями доступных масштабов (рис. 6.7).

 

 

Рис. 6.7 Переключатели масштабов

Обновление экрана

Для их устранения следует использовать команду «обновить» (Refresh) меню «Вид» (View). Эта команда никак не влияет на объекты документа, а лишь уничтожает следы от… Команда полезна также в тех случаях, когда часть текстового блока не видна из-за наложения на него другого блока –…

Линейка форматирования

В ней представлены наиболее важные команды только из одного меню – форматирования, определяющего внешнюю форму напечатанного документа. При помощи линейки форматирования можно выбрать требуемый вид, размер и… При установке курсора на значке под ним появляется надпись, раскрывающая его назначение, а при одном щелчке…

Вопросы для самоконтроля

2. Записи констант, переменных величин, комплексных чисел, функций, стандартных функций, знаков равенства 3. Содержание текстового окна MathCAD 4. Назначение курсора ввода

Удаление математических выражений

Удаление отдельных символов осуществляется с помощью клавиш «Backspace» (Бекспейс) (←). При этом визир следует ставить после удаляемого… Удаление одного математического выражения, например уравнения, осуществляется… Сначала следует с помощью левой клавиши мыши очертить это выражение пунктирной линией, которая затем превращается в…

Копирование математических выражений

Сначала необходимо с помощью левой клавиши мыши очертить всю копируемую группу выражений пунктирной линией, после чего каждое из них будет окружено… Второе действие может быть осуществлено одним из двух способов: 1. путем обращения к команде «Копировать» на стандартной линейке или в меню «Правка»;

Перенос математических выражений

2-й вариант: необходимо с помощью левой клавиши мыши очертить всю копируемую группу выражений пунктирной линий, после чего каждое из них будет… Затем подвести курсор-стрелку к любой из пунктирных линий и дожидаться… Далее, не снимая пальца с левой клавиши мыши, следует перетянуть всю группу выражений в требуемое место рабочей…

Вписывание в программу текстовых комментариев

После ввода с клавиатуры символа “ (кавычки) в месте нахождения красного визира появится прямоугольник, в который и вводится требуемый текст в… Редактирование введенного текста может быть осуществлено с помощью подменю… Удаление, копирование и перенос текстовых комментариев осуществляется по той же методике, что и математических…

Вопросы для самоконтроля

1. Правила удаления математических выражений.

2. Правила копирования математических выражений.

3. Правила переноса математических выражений.

4. Правила вписывания в программу текстовых комментариев.

 

Построение графиков

При построении графиков можно воспользоваться инструментальной панелью «График» из меню «Вид» или подменю «График» в меню «Вставка». С их помощью можно построить двухмерные графики в декартовой и полярной… Рассмотрим сначала на конкретном примере методику построения двухмерного графика в декартовой системе координат.

Построение графиков в декартовой системе координат

 

Пример 1

 

Требуется построить график функции:

 

Y(t) = β · e^{(–α · t)} · sin ( 2 · π · F1 · t) ,

 

в пределах изменения аргумента t от 0 до 5 при:

 

β = 10, F1 = 5, α = 0.5,

 

Вызываем панели «Арифметика» и «Греческий алфавит».

В рабочей области текстового окна в месте установки красного визира записываем согласно правилам MathCAD исходные данные и функцию:

 

 

 

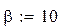
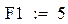
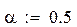
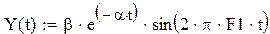
Вызываем панель «Графики», щелчок по пиктограмме «Декартов график», в месте установки красного визира появляется прямоугольная рамка с осями абсцисс и ординат.

График должен располагаться ниже формулы.

На месте черного квадратика, расположенного внизу оси абсцисс вписываем имя аргумента – t, а слева от оси ординат – имя функции Y(t).

Устанавливаем требуемые крайние значения аргумента по оси абсцисс (0…5) и функции по оси ординат (-10…10).

После щелчка вне прямоугольной рамки происходит автоматическое построение графика.

Установив курсор внутри прямоугольной рамки, двумя щелчками левой клавиши «мыши» вызываем диалоговое окно, позволяющее выбирать:

· вид масштаба по осям (равномерный или логарифмический);

· количество вспомогательных линий координатной сетки;

· толщину, вид и цвет графика.

В результате получаем график заданной функции, представленный на рис. 6.26.

 

 

Рис.6.26 График функции Y(t)

 

Пример 2

 

Требуется построить график полинома Чебышева 1-ого рода 6-го порядка:

F(x) = 32 · x⁶ – 48 · x⁴ + 18 · x² –1

 

в пределах изменения аргумента х от -2 до +2.

Вызываем панель «Арифметика». В рабочей области текстового окна в месте установки красного визира записываем согласно правилам MathCAD исходную функцию:

 

 

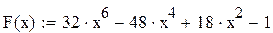
Вызываем панель «График», делаем щелчок по пиктограмме «Декартов график». В месте установки красного визира появляется прямоугольная рамка с осями абсцисс и ординат.

График должен располагаться ниже формулы (рис. 6.27).

 

 

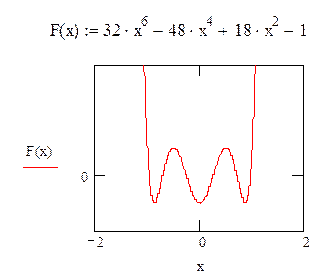
Рис.6.27 График полинома Чебышева

 

На месте черного квадратика, расположенного внизу оси абсцисс, вписываем имя аргумента – х, а слева от оси ординат – имя функции F(x).

Устанавливаем требуемые крайние значения аргумента по оси абсцисс и функции по оси ординат.

После щелчка вне прямоугольной рамки происходит автоматическое построение графика.

Установив курсор внутри прямоугольной рамки, двумя щелчками левой клавиши «мыши» вызываем диалоговое окно:

· выбираем логарифмический масштаб по оси ординат;

· количество линий координатной сетки;

· толщину, вид и цвет графика.

Можно построить графики заданной функции при равномерном и логарифмическом масштабе по оси ординат.

 

 

Построение графиков в полярной системе координат

Построение графиков в полярной системе координат рассмотрим на практике. Пусть требуется построить в полярной системе координат график функции… ,  

Изменение формата графиков

Эти маркеры имеют вид маленьких черных прямоугольников. Указатель при этом приобретает форму двухсторонней стрелки, указывающей, в… Нажав левую кнопку мыши и захватив соответствующую сторону или угол шаблона рисунка, можно не отпуская кнопки,…

Правила трассировки графиков

Если щелкнуть в области графика правой кнопкой мыши, появляется меню. В нем есть команда Tracy (трассировка). Эта команда выводит окно трассировки…  

Правила просмотра участков двумерных графиков

Некоторые графики представляют собой довольно сложные кривые. Для детального просмотра любого участка графика следует выделить график, поместить в…  

Вопросы для самоконтроля

2. Правила построения графиков в полярной системе координат 3. Изменение формата графиков 4. Правила трассировки графиков

Примеры

1. Вычислить косинус угла, равного 0,5 радиана.

Вызываем панель «Арифметика», щелчок по кнопке «cos». В рабочей области текстового окна появляется выражение:

 

cos ( )

 

Вписывается внутрь скобок число 0,5 – получаем:

 

cos (0.5)

 

Вводим знак ( = ), после чего автоматически получаем результат:

 

cos (0.5) = 0.878

 

В меню математика должен стоять автоматический расчет (либо щелкнуть «вычисление») (автоматическое вычисление).

 

2. Вычислить определенный интеграл от функции sin²(x) в пределах изменения аргумента от 0,5 до 2.

Вызываем панель «Матанализ» («Исчисления»), щелчок по пиктограмме, на которой изображен определенный интеграл.

В рабочей области текстового окна в месте установки красного визира появляется выражение:

 

 

Вписываем в него значения верхнего и нижнего пределов интегрирования, а под знаком интеграла заданную функцию, вводим знак =, после чего автоматически получаем результат:

 

 

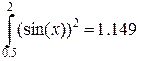
3. Получить из заданной матрицы размером 3х3 транспонированную матрицу.

Вызываем панель инструментов «Матрица» (меню «Вид» → подменю математика).

На ней делаем щелчок по пиктограмме, на которой изображена матрица.

В рабочей области текстового окна в месте установки красного визира появляется диалоговое окно, в котором после слов «строки» и «столбцы» вписываем заданные числа: 3 и 3.

После нажатия на кнопку «ОК» или «Вставить» в тексте программы появляется матрица выбранной размерности. Вписываем в ячейки матрицы требуемые числа.

Обрамляем с помощью курсора всю запись пунктирной линией и щелкаем по пиктограмме M^Т, означающей выполнение операции по транспонированию матрицы.

Вводим знак равенства, после чего автоматически получаем результат:

 

Вызов матрицы можно также произвести путем обращения к подменю «Матрица» из меню «Вставка».

 

Правило 2 – связанное с обращением к встроенным функциям f(x) из меню «Вставка», либо к пиктограмме «Встроенная функция f(x)» на 2-ой строке текстового окна – стандартной линейке.

Результат будет получен в виде числа. На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбирается определенное имя, тип функции, а в разделе «Название функции» - требуемая функция

После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна появляется выбранная функция, в которую вписываются заданные числа, и вводится знак «=», после чего автоматически получается результат.

 

Пример

Вычислить функцию Бесселя 1-ого рода 1-ого порядка при аргументе 5.

Обращаемся к пиктограмме встроенная функция f(x) на 2-ой строке текстового окна – стандартной линейке.

На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Бесселя», а в разделе» Название функций» - I 1.

После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна в месте установки красного визира появляется выражение I 1 ( ■ ).

Вписываем внутрь скобок заданное значение аргумента – I 1 (5) – и вводим знак =, после чего автоматически получаем результат: I 1 (5) = 24.336

Правило 3

Данное правило, по существу, аналогично двум предыдущим. Только здесь все знаки – числа, арифметические действия и латинские… Возможен ввод и специальных операторов при символьных вычислениях путем одновременного нажатия двух или трех клавиш. …

Правило 4

1. Математическое выражение, подлежащее преобразованию, записывается в рабочей области текстового окна и с помощью курсора обрамляется рамкой. 2. Далее в зависимости от вида преобразования выбирается соответствующее… · Ряд – при разложении функции в степенной ряд Маклорена по выбранной переменной;

Примеры

1

2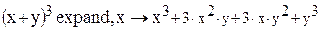

 

3

 

4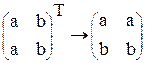

 

5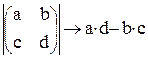

 

6

 

Правило 5

Математические выражения, связанные между собой определенными операциями, записываются в рабочей области текстового окна, и с помощью курсора… Далее щелчком производится обращение к строке «символические» при… После щелчка на рабочем столе появляется результат в виде нового выражения, располагаемого под исходной записью.

Примеры

1.

 

 

Используется подменю «Расчеты», опция «символические»

2.

 

 

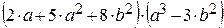
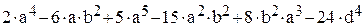
Используется подменю «Расширить»

 

3.

 

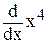
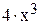
4.

 

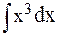
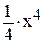
Используется опция «Символические»

 

Правило 6

Позволяет произвести разнообразные символьные преобразования, записав в рабочей области текстового окна подлежащее преобразованию выражение. При обращении к подменю «Переменные» в этом выражении необходимо выделить… Далее с помощью подменю «Переменные» можно выполнить следующие операции:

Вопросы для самоконтроля

1. Первое правило решения математических задач в среде MathCAD

2. Второе правило решения математических задач в среде MathCAD

3. Третье правило решения математических задач в среде MathCAD

4. Четвертое правило решения математических задач в среде MathCAD

5. Пятое правило решения математических задач в среде MathCAD

6. Шестое правило решения математических задач в среде MathCAD

Анализ линейных устройств

Иногда нелинейные устройства могут рассматриваться как линейные при относительно малой амплитуде входного сигнала (не выходит за пределы линейных… Математической основой анализа линейных устройств является система линейных… Поиск решений базируется на преобразовании Лапласа (временный подход), или Фурье (спектральный анализ).

Передаточная функция, коэффициент передачи, временные и частотные характеристики

Передаточная функция устройства K(p), позволяющая найти временные характеристики определяется согласно преобразованию Лапласа. Согласно преобразованию Фурье определяется коэффициент передачи K(jω),… МеждуK(p)и K(jω) существует прямая связь, позволяющая от временных характеристик перейти к частотным и обратно. …

Амплитудно-частотная характеристика (АЧХ)

   

Программа расчета частотных характеристик цепи

Определение переходной и импульсной характеристик

Это есть зависимость выходного сигнала Y(t) от времени при входном сигнале в виде единичной функции: l(t)=1 при t≥0 l(t)=0 при t<0

Импульсная характеристика h(t)

  ,  

Вопросы для самоконтроля

2.Дать понятие амплитудно-частотной характеристики линейного устройства 3.Дать понятие фазо-частотной характеристики линейного устройства 4.Дать понятие переходной характеристики линейного устройства

Определение корней алгеброических уравнений

  F(x) = 0 (6.1)  

Методы решения алгебраических уравнений в среде MathCAD

Возможны 2 способа нахождения корней уравнения (6.2) в среде MathCAD:

· с помощью методов символьной математики согласно правилу 6;

· путем обращения к встроенной функции согласно правилу 2.

Рассмотрим применение обоих методов на конкретных примерах.

 

Пример

Найти корни кубического уравнения:

 

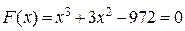(6.3)

 

Решение по правилу 6:

Открываем рабочий лист и записываем многочлен из уравнения (6.3):

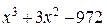
Выделяем (затемняем ■) в этом многочлене в любом члене один символ – переменную x – путем протаскивания курсора.

Открываем меню «Символ», подменю «Переменные» (Variable), щелчок по опции «Вычислить» (Solve).

На рабочем листе появляется результат, записанный в форме вектора:

 

 

 

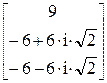
Решение по правилу 2:

Вновь записываем многочлен из уравнения (6.3):

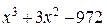
Выделяем (затемняем ■) в этом многочлене в любом члене один символ переменной х – путем протаскивания курсора.

Записываем вектор коэффициентов многочлена, для чего открываем меню «Символ», щелчок по опции «Коэффициенты» (Polynomial Coefficients).

Перед вектором вставляем его имя V:= . Получаем результат:

 

Следует отметить, что при отсутствии какого-либо члена, соответствующий ему коэффициент принимается равным 0.

Обращаемся к пиктограмме «Встроенная функция» f(x) на второй строке текстового окна – стандартной линейке.

На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Решение» (All), а в разделе «Название функции» – polyroots (корни полинома).

После нажатия на кнопку «ок» или «Вставить» на рабочем листе появляется название данной функции.

В скобки вписываем имя вектора коэффициентов V и вводим знак =.

После ввода знака равенства получаем результат в виде вектора:

 

,

 

Точность полученного результат устанавливаем путем открытия меню «Формат», подменю «Результат» и выбора требуемого числа десятичных знаков в открывшемся окне.

Проводим проверку полученных результатов.

Для этого последовательно при каждом из полученных значений корня x_i (переносим их методом копирования) вычисляем значение многочлена F(x).

Близость к нулю действительной и мнимой частей F(x) указывает на правильность полученных результатов:

 

check-up

 

 

 

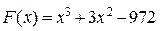
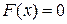
Определение корней трансцендентных уравнений

Уравнение F(x)=0 называется трансцендентным, если хотя бы одна из функций в нем не является алгебраической.

 

Пример

 

(6.4)

 

Регулярных аналитических методов решения трансцендентных уравнений не существует. В каждом конкретном случае ищется свой индивидуальный прием.

Общим является только графический метод, состоящий в построении графика функций F(x).

Точки пересечения построенного графика с осью абсцисс и есть искомые действительные корни уравнения.

В среде MathCAD возможны два способа нахождения корней уравнения (6.4)

· с помощью методов символьной математики согласно правилу 6;

· с помощью встроенной функции root в подменю f(x) меню «Вставка» согласно правилу 2.

Рассмотрим применение обоих методов на примере нахождения корней уравнения (6.4).

Поскольку неизвестно решение (значения х, при которых F(x)=0), то строим его график с целью приблизительного определения искомого действительного решения.

 

х := -10 … +10

 

 

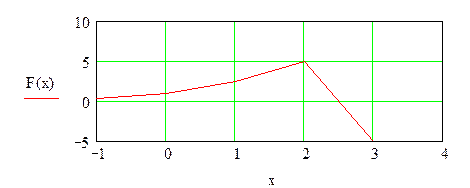
Рис. 6.35 Графическое решение

 

Из графика видно, что это решение, определяемое как точка пересечения графика с осью абсцисс, лежит в промежутке значений х = 2…3.

Решение по правилу 6

Записываем многочлен из уравнения (6.4):

 

 

Выделяем (затемняем ■) в этом многочлене в любом месте символ переменной х – путем протаскивания курсора.

Открываем меню «Символ», подменю «Переменные» и делаем щелчок по опции «Вычислить».

На рабочем листе получается результат:

 

 

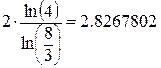
Решение по правилу 2:

Записываем уравнение:

Вводим любое имя искомого решения и знак присвоения, например:

r := ,

после которого размещаем красный визир ±.

Обращаемся к пиктограмме «Встроенная функция f(x)» на 2-ой строке текстового окна – стандартной линейке.

На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Решение», а в разделе «Название функций» - root (корни). После нажатия на кнопку «ок» или «Вставить» на рабочем листе появляется название данной функции с четырьмя черными прямоугольниками, которые следует заполнить:

 

r := root (■, ■, ■, ■)

 

В первое окошко вписываем имя функций F(x), во второе – переменную х, в третье и четвертое – (а) нижний и (в) верхний пределы, внутри которых ищется решение. Запись приобретает вид:

 

r: = root (F(x), x, a, в) ,

(пределы согласно рисунку 6.1 установлены 0 и 3).

Вновь вводим искомое решение, но теперь со знаком равенства:

 

r = ,

и сразу получаем результат.

 

r = 2,8267802

 

Точность полученного результата устанавливаем путем открытия меню «Формат», подменю «Результат» и выбора требуемого числа десятичных знаков в открывшемся окне.

Проводим проверку полученного результата, для чего вычисляем значение функции F(x) при найденном значении корня.

 

x := 2.8267802

 

F(x) = 2.287 · 10^-7

 

Близость к нулю функции F(x) указывает на правильность полученного результата.

 

Вычисления по циклу

При этом результаты расчета следует представить в виде массива чисел, заключив их в определенную таблицу. При подобных многократных расчетах по одной и той же формуле или алгоритму… · во-первых, выбрать «шаг» или дискрет изменения аргумента;

Пример циклического расчета

Рассчитать с «шагом» 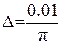затухающий колебательный процесс, описываемый функцией:

 

,

 

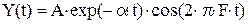при А = 10, α = 0,5, F = 10 и N = 1000.

Организуем цикл расчета с помощью записи k := 0…N и выражений для аргумента t_k и дискретной функции Y_k(t_k), полученной из непрерывной функции Y(t).

 

 

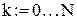
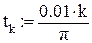
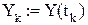
Строим график дискретной функции :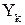

 

 

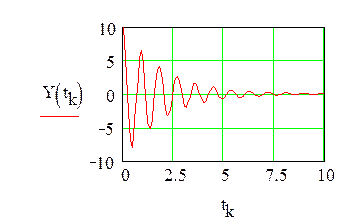
Рис.6.36 График дискретной функции

 

Вывод в виде таблицы дискретных значений осуществляется путем записи Y= или .

По умолчанию на рабочий лист выводится 16 значений функции.

Щелкнув по графику функции, обрамляют ее рамкой и путем протаскивания вниз курсора расширяют таблицу до любого требуемого значения k≤N.

При протаскивании курсора вверх таблица наоборот сжимается.

Таким же образом можно вывести и таблицу значений аргумента, сделав в рассматриваемом случае запись .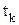

 

Вопросы для самоконтроля

1. Способы определения корней алгебраических уравнений в среде MathCAD

2. Способы определения корней трансцендентных уравнений в среде MathCAD

3. Способы организации вычислений по циклу

 

Обработка данных

При решении многих задач в радиотехнике, исходная функция задается в табличной форме или по точкам (например, экспериментально полученные… «MathCAD» располагает двумя способами интерполяции: · кусочно-линейной;

Кусочно-линейная интерполяция

При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Для этого используется функция linterp (VX, VY, x). Для заданных векторов VX и…  

Пример

Пусть экспериментально получена амплитудная характеристика усилителя (таблица 6.1)

Таблица 6.1

Uвх(В)		0.05	0.1	0.2	0.3	0.4	0.5	0.6
Uвых(В)	0.001	0.1	0.2	0.4	0.5	0.55	0.57	0.575

 

В программной среде «MathCAD» исходная функция (U_ВЫХ=F(U_ВХ)) записывается в виде матрицы [2x8]:

 

 

 

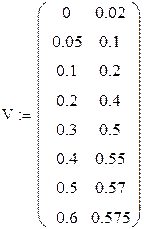
Далее производится сортировка значений функции по возрастанию значений аргумента, если в таблице такая сортировка не произведена. Для этого обращаемся к встроенным функциям f(x), (например, на стандартной линейке).

Записываем:

V:=

 

Открываем окно f(x) и выбираем в разделе категория функций – «сортировка», а в разделе имя функции – «сортировка по аргументу» (csort (v, o)).

После щелчка на кнопке «ок» получим запись:

 

,

 

далее вставляем имя матрицы:

 

V:= csort (V,0)

 

Далее присваиваем значениям аргумента значения из первого столбца:

 

,

 

а значениям функции значения второго столбца:

 

 

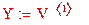
Теперь можно провести кусочно-линейную интерполяцию.

Записываем:

 

W(x):=

 

Открываем окно встроенных функций. В разделе «категория функций» указываем название «интерполяция», а в разделе «имя функции» – «линейная» («linterp»). После щелчка по клавише «ок» появляется запись:

 

 

Вводим в скобки последовательно X,Y,x:

 

W(x):= linterp(X,Y,x)

 

Далее по правилам построения графиков строим зависимость W(x) = f(x) (Рис. 6.38).

 

 

Рис.6.37 График зависимости W(x) = f(x)

 

Сплайн-интерполяция

Часто хорошие результаты дает сплайн-аппроксимация отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты… cspline (VX, VY) – возвращает вектор VS вторых производных при приближении в… pspline (VX, VY) – возвращает вектор VS вторых производных при приближении к опорным точкам отрезками парабол;

Экстраполяция

В математике экстраполяцией называется предсказание поведения некоторой зависимости по имеющимся измерениям ее характеристики в определенной, иногда… В MathCAD экстраполяция основывается на анализе поведения зависимости в… Функцией, реализующей алгоритм линейной экстраполяции является встроенная функция

Вопросы для самоконтроля

1. Понятие об интерполяции и экстраполяции

2. Понятие о кусочно-линейной интерполяции

3. Способ реализации кусочно-линейной интерполяции в среде MathCAD

4. Понятие о сплайн-интерполяции

5. Способ реализации сплайн-интерполяции в среде MathCAD

 

 

Символьные вычисления

Первый, символьный или аналитический, известен с глубокой древности. Второй, численный, получил широкое распространение только во второй половине… Решение задач аналитически имеет массу преимуществ перед решением численным:

Пример

Решить уравнение x² – a = 0

Используя панель «Символика» запишем:

 

x² – a solve, x →

Результат получим в виде вектора:

 

Символьные преобразования, осуществляемые при помощи операторов панели «Символика» более наглядны, чем при использовании команд соответствующего меню.

Посмотрим на примерах отличия символьных преобразований при использовании панели и меню. Главное отличие – это то, что преобразования при помощи команд меню осуществляются MathCAD без учета определений и присваиваний, сделанных в документе выше.

При использовании же операторов панели «Символика» происходит подстановка определенных выше значений параметров.

 

Пример

Необходимо разложить в ряд функцию cos(ax + b), при a = 3 и b = 5.

Разложение в ряд при помощи команды меню «Символические» дает:

 

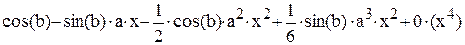
При использовании же операторов панели «Символика» происходит подстановка значений введенных параметров a и b:

 

 

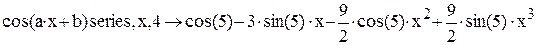
Очевидно, что использование команд меню удобнее тогда, когда результат не нужно сохранять или использовать в дальнейших расчетах. В противном случае лучше применять операторы панели «Символика».

Однако меню «Символические» имеет ряд команд и настроек, которые не находят отражения на рабочей панели.

Одной из особенностей этого меню является наличие в нем подменю «вычислить» (Evaluate), отвечающего за проведение арифметических расчетов при помощи символьного процессора.

Состав подменю «Вычислить»:

 

Символические	(Symbolically)
Плавающая точка	(Floating Point)
Комплексные	(Complex)

 

Данное меню содержит три команды.

В первой строке располагается команда «Символически» (Symbolically), предназначенная для расчета значения некоторой функции или выражения в символьном виде. По своему назначению она полностью совпадает с оператором символьного вывода «→». Эта же команда может быть задействована нажатием сочетания клавиш [«Shift» + «F9»] (при этом вычисляемое выражение должно быть выделено).

Пример

Необходимо вычислить

Нажав [Shift + F9] получим:

,

 

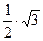либо, используя оператор символьного вывода:

 

 

В меню «Символы», подменю «Расчеты» расположена команда «Плавающая точка» (Floating Point). С ее помощью можно получить численное значение некоторого выражения с нужной точностью.

Чтобы это сделать, необходимо выделить выражение и нажать данную команду. На экране появится специальное окно настройки «Вычисления с плавающей запятой» (рис. 6.40).

 

 

Рис. 6.40 Команда «Вычисления с плавающей запятой»

 

В строке «Floating Point Precision» необходимо задать уровень по шкале от 1 до 4000.

Примеры использования команды «Плавающая точка»: Найдем значение следующего выражения при различных уровнях точности:

 

.

 

Floating Point Precision = 3:

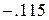
Floating Point Precision = 15:

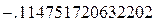
Floating Point Precision = 20:

 

Для обычных выражений увеличение уровня точности от 20 и выше не приводит к каким либо изменениям в ответе, поскольку числа с дробной частью при символьных расчетах отображаются только до 20-го знака после запятой. Однако уровень точности 4000 может понадобиться в том случае, если вы работаете с очень малыми величинами.

Арифметические расчеты с помощью символьного процессора могут быть полезны, если величина результата меньше параметра «Порог нуля» («Zero Threshold») закладки «Точность» («Tolerance») меню «Формат результата» («Result Format»).

В этом случае при использовании оператора численного вывода « = » в качестве ответа будет выдан ноль. Вычисление же символически даст правильный результат.

 

Пример

Точность результата при различных типах расчета.

«Порог нуля» («Zero Threshold») = 10^-10

 

 

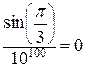
Использование команды «Плавающая точка»:

 

8,6602540378443864675 · 10^-101

 

В меню «Символы», подменю «Рсчеты» расположена команда «Комплексные» (Complex), при помощи которой можно производить перевод различных форм записи комплексных чисел к стандартной (вида a + i · b).

 

Пример

;

.

 

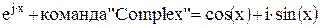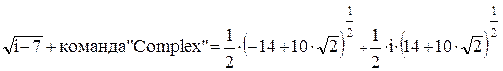Произвести настройку особенностей отображения результата при использовании для символьных расчетов меню «Символические» (Symbolics) можно при помощи специального подменю «Стиль вычислений» (Evaluation Style) (рис. 6.41).

 

 

Рис 6.41 Подменю «Стиль вычислений»

 

При помощи параметров списка «Отображение шагов вычисления» (Show evaluations steps) рассматриваемого меню можно определить, каким образом по отношение к исходному выражению будет выведен результат символьных расчетов.

Данный список содержит 3 пункта:

1 «Вертикально, вставляя линии» (Vertikally, inserting lines). Параметр, определенный по умолчанию. Результат вставляется в специальную, очищенную от других формул полосу рабочей области ниже исходного выражения. Остальные объекты листа при этом смещаются вниз на ширину данной полосы;

2 «Вертикально, не вставляя линий» (Vertically, without inserting lines).

Результат выводиться ниже исходного выражения, но это не сказывается на положении других формул документа;

3 «Горизонтально» (Horizontally). Результат отображается правее исходного выражения.

Если поставить флажок в окошке «Вычислить на месте» (Evaluate In Place), то результат просто заменит исходное выражение.

При включении параметра «Показать комментарии» (Show comments) ответ выводиться на лист вместе с текстовой строкой, содержащей информацию о проделанной символьной операции.

 

Пример

x² – 4x + 1, выделим х и проведем интегрирование. В результате выводятся комментарии и результат интегрирования:

 

by integration, yiecds

 

 

Упрощение вида ответа при символьных расчетах

Чтобы упростить вид ответа, достаточно после вектора результата поставить оператор численного вывода « = ». При этом сложные подкоренные и степенные…  

Пример

Зависимость величины корня кубического уравнения 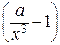от значения коэффициента a.

Запишем: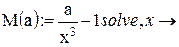

Получим: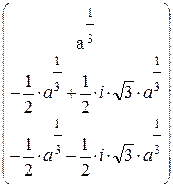

 

Обозначим: x(a):=M(a)_o и построим график x(a):

 

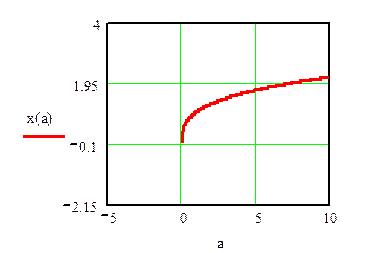
Рис. 6.42 График x(a)

 

Глядя на график можно заметить следующее:

Действительное решение равно значению параметра в степени , поэтому оно должно принимать и отрицательные значения.

По правилам алгебры:

 

,

 

а извлечь кубический корень можно из любого действительного числа, и поэтому соответствующая функция должна быть определена на всей числовой оси:

 

 

График этой функции представляем на рис. 6.43.

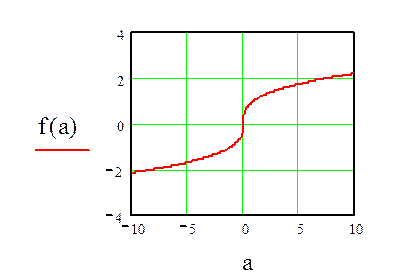
Рис. 6.43 График функции f(a)

 

Вопрос: почему же кривая x(a) (Рис. 8.3) не существует при отрицательных значениях параметра a?

Все дело в существовании одного очень тонкого отличия в MathCAD между записью кубического корня в виде непосредственного математического оператора и как степени.

Разница эта заключается в том, что оператор рассматривает подкоренное выражение как действительное число, а степень – как комплексное.

При этом, если операция проводится над действительным отрицательным числом, то в первом случае ответ будет также действительным отрицательным числом, а во втором – комплексным выражением.

При возведении и того, и другого ответа в куб будет получено, в рамках рабочей точности, исходное число.

Аналогичная ситуация существует и для корней других нечетных степеней:

 

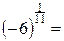(1,12923107663412 + 0,331572160749093i)

 

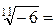-1,17690395624285

 

(1,12923107663412 +0,331572160749093i)¹¹= -5,99999999999994

 

(-1,17690395624285)¹¹= -5,99999999999985

 

Таким образом запись в виде при n-нечетном позволяет получить значения корня в виде действительного числа.

 

Вопросы для самоконтроля

2. Достоинства и недостатки этих двух методов 3. Состав подменю «ВЫЧИСЛИТЬ» меню «СИМВОЛИЧЕСКИЕ» 4. Назначение подменю «СТИЛЬ ВЫЧИСЛЕНИЙ» меню «СИМВОЛИЧЕСКИЕ»

Оптимизация в расчетах РЭА

Оптимизация есть процедура поиска и нахождения такой комбинации значений параметров устройства определенной структуры, при которой характеристики… Инженерное проектирование устройства, превосходящего по своим параметрам… Оптимизация в сочетании с перебором определенного числа структур проектируемого объекта перерастает в процедуру…

Стратегии одномерной оптимизации

Типы одномерных функций. Одномерная оптимизация относится к наиболее простому типу оптимизационных задач. Однако их более детальный анализ… В инженерной практике приходится использовать как непрерывные, так и разрывные…

Локальные и глобальные экстремумы

Функция f(х), определенная на множестве S, достигает своего глобального минимума в точке x**Î S в том и только том случае, если f(x**) £ f(x) для всех xÎ S. Функция f(х), определенная на множестве S, имеет локальный, ми­нимум (относительный минимум) в точке x*Î S в том…

Методы включения интервалов неопределенности

В разд. 4.2 рассматривался вопрос анализа «в статике», который заключается в том, чтобы определить, является ли данное решение оптимальным. Для… В разд. 4.2. было дано определение унимодальной функции. Уни­модальность…

Теорема

1. Если f(х1)>f(х2), то точка минимума f(x) не лежит в интервале (a, х1), т. е. х* Î(х2, b) (рис. 6.49 а). 2. Если f(х1)<f(х2), то точка минимума не лежит в интервала (х2, b), т. е.… Доказательство

Пример метода золотого сечения

Опять рассмотрим задачу из примера 2.6, в которой требуется минимизировать f(х)=(100-х)² в интервале 60£х£150. Для того чтобы перейти к интервалу единичной длины, проведем замену переменной, положив w=(х - 60)/90. Таким образом, задача принимает следующий вид: минимизировать f(w) = (40 – 90w)² при ограничении 0£w£1.

Итерация 1. I₁ = (0, 1); L₁ = l. Проведем два первых вы­числения значений функции:

w₁ = t = 0,618, f(w₁) = 244,0

w₂ = 1-t = t² = 0,382, f(w₂) = 31,6

Так как f(w₂) < f(w₁) и w₂ < w₁, интервал w ³ w₁ исключается.

Итерация 2. I₂ =(0. 0,618); L₂ = 0,618 = t. Следующее вы­числение значения функции проводится в точке

w₃ = t-t² = t(1-t) = t³ = 0,236, f(w₃) = 352.

Так как f(w₃) > f (w₂) и w₃ < w₂, интервал w £ w₃, исключается.

Итерация 3. I₃ =(0,236, 0,618); L₃ = 0,382 = t². Следующее вычисление значения функции проводится в точке, расположенной на расстоянии t ´ (длина полученного интервала) от левой гра­ничной точки интервала, или на расстоянии (1-t) ´ (длина ин­тервала) от правой граничной точки. Таким образом,

w₄ =0,618 – (1-t)L₃ = 0.618 - t² L₃ 0.618 - t²(t²) = 0.618 - t⁴ = 0,472, f(w₄) = 6,15.

Так как f(w₄) < f (w₂) и w₄ > w₂, интервал w £ w₂ исключается.

В результате получен следующий интервал неопределенности: 0,382 £ w £ 0,618 для переменной w, или 94,4£х£115,6 для перемен­ной х.

Если в процессе поиска проведено шесть вычислений значений функции, то длина результирующего интервала для переменной w равна

t_N-1 = t₅ = 0,09,

что соответствует интервалу длины 8,1 для переменной х. Для срав­нения напомним, что в аналогичной ситуации метод деления интер­вала пополам привел к получению интервала длины 11,25.

В общем случае если правая и левая граничные точки интервала неопределенности (обозначим их через XR и XL) известны, то ко­ординаты всех последующих пробных точек, получаемых в соответ­ствии с методом золотого сечения, можно вычислить по формулам

w = XR - tⁿ или w = XL + tⁿ, в зависимости от того, какой подынтервал был исключен на преды­дущей итерации – левый или правый. В приведенных выше форму­лах через tⁿ обозначена n-я степень t, где п – количество вычисле­ний значений функции.

Поиск с помощью метода золотого сечения может быть окончен либо исходя из заданного количества вычислений значений функ­ции (и, следовательно, величины интервала неопределенности), либо по достижении относительной точности искомого значения функции. Наиболее предпочтительным является использование обоих критериев одновременно.

Сравнение методов исключения интервалов. Ниже проводится сравнение относительных эффективностей рас­смотренных методов исключения интервалов. Обозначим длину неходкого интервала неопределенности через L₁, а длину интервала, получаемого в результате N вычислений значений функции, - через L_N. В качестве показателя эффективности того или иного метода исключения интервалов введем в рассмотрение характеристику относительного уменьшения исходного интервала FR(N)=L_N/L₁

Напомним, что при использовании метода деления интервала пополам и метода золотого сечения длина получаемого интервала составляет L₁(0,5)^N/2 и L₁(0.618)^N-1 соответственно. Следовательно, относительное уменьшение интервала после N вычислений значений функции равно

FR(N) = (0,5)^N/2 для метода деления интервала пополам;

FR(N) = (0,618) ^N-1 для метода золотого сечения.

Для сравнения рассмотрим также метод равномерного поиска, в соответствии с которым оценивание функции проводится в N равноотстоящих друг от друга точках (при этом интервал L₁ де­лится на (N+1) равных интервалов длины L₁/(N+l)). Пусть х* – точка, в которой наблюдается минимум функции f(х). Тогда точка истинного минимума f(x) оказывается заключенной в интервале

 

,

 

откуда L_N = 2L₁/(N+l). Следовательно, для метода равномерного поиска FR(N)=2/(N+1).

В табл. 6.2 представлены значения FR(N), соответствующие выбранным N, для трех методов поиска. Из таблицы следует, что поиск величины относительного уменьшения интервала с помощью метода золотого сечения

 

Таблица 6.2

Метод поиска	Количество вычислений значений функции
N=2	N=5	N=10	N=15	N=20
Метод деления интервала пополам	0,5	0,177	0,031	0,006	0,0009
Метод золотого сечения	0,618	0,146	0,013	0,001	0,0001
Метод равномерного поиска	0,667	0,333	0,182	0,125	0,095

 

обеспечивает наибольшее от­носительное уменьшение исходного интервала при одном и том же количестве вычислений значений функции. С другой стороны, можно также сравнить количества вычислений значения функции, требуе­мые для достижения заданной величины относительного уменьшения интервала или заданной степени точности. Если величина FR(N) = E задана, то значение N вычисляется по следующим формулам:

для метода деления интервала пополам

N=2 ln(E)/ln(0,5),

для метода золотого сечения

N=1+[ln(E)/ln(0,618)],

для метода равномерного поиска

N=(2/E)-1

В табл. 6.3 приведены данные о количествах вычислений значений функции, необходимых для определения координаты точки мини­мума с заданной точностью. Следует еще раз подчеркнуть, что метод золотого сечения оказывается более эффективным по сравнению с остальными двумя методами, поскольку он требует наименьшего числа оцениваний значения функции для достижения одной и той же заданной точности.

Требуемые количества вычислений значений функции

Таблица 6.3

Метод поиска	Заданная точность
Е=0,1	Е=0,05	Е=0,01	Е=0,001
Метод деления интервала пополам
Метод золотого сечения
Метод равномерного поиска

 

Критерии оптимизации

Важная сторона оптимизации – это выбор критерия, по которому определяются свойства объекта и который позволяет количественно оценить какое из… Критерии в зависимости от назначения устройства могут быть самыми разными. Так при проектировании фильтра критерий может относиться к его амплитудно-частной характеристике, минимуму потерь в…

Методы поиска экстремума функции цели

Скалярное значение функции цели (9.7) в пределах возможного изменения вектора x может иметь несколько или множество локальных минимумов и один… Сами методы поиска целевой функции, т.е. определение xопт , классифицируется… · по виду искомого минимума – локальные и глобальные;

Пример записи целевой функции при синтезе фильтров

Проектирование фильтра осуществляется путем процедуры синтеза, включающего два этапа – аппроксимацию и реализацию, исходя из заданных полос пропускания и заграждения, и потерь в них. На первом этапе – аппроксимации – производится замена требуемой характеристики затухания фильтра функцией Чебышева или Баттерворта, либо иной зависимостью отвечающей условиям физической реализуемости. На втором этапе – реализация – определяется структура и параметры элементов фильтра.

Применение компьютера позволило изменить данный подход к синтезу фильтров, имеющих ряд ограничений, и повысить точность расчетов за счет возможности учета ряда факторов.

При компьютерном подходе аппроксимация и реализация заменяются процедурой оптимизации. Производится непосредственный расчет характеристик фильтра на основе определенных рекуррентных соотношений. Осуществляется перебор нескольких типовых структур фильтров и оптимизации параметров в каждом варианте на основе поисковых методов глобального и локального минимума целевой функции.

При таком подходе процедура синтеза представляется как множество вариантов анализа с поиском наилучшего из них согласно определенному критерию. Такая методика предусматривает огромный объем рутинных вычислений, поэтому практическая реализация возможна только с применением компьютера.

При составлении программы параметрического синтеза фильтра функция цели, подлежащая минимизации, может быть представлена в следующем виде:

 

 

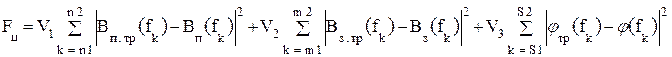
f_n1..f_n2 – полоса пропускания;

f_m1..f_m2 – полоса заграждения;

f_S1..f_S2 – полоса частот фазовой характеристики;

B_п(f_k) – полученное затухание фильтра в полосе пропускания на частоте f_k ;

B_п.тр(f_k) – требуемое затухание фильтра в полосе пропускания;

B_з(f_k) – полученное затухание фильтра в полосе заграждения на частоте f_k ;

B_з.тр(f_k) – требуемое затухание фильтра в полосе заграждения;

φ (f_k) – полученное значение ФЧХ на частоте f = f_k;

φ_тр (f_k) – требуемое значение ФЧХ на той же частоте f = f_k;

V₁, V₂, V₃ – коэффициенты веса, определяющие соотношение требований по затуханию, предъявляющих к полосам пропускания и заграждения, а также другим параметрам.

В качестве примера можно привести задачу минимизации порядка фильтра, обеспечивающего требуемые значения затухания в полосах пропускания и заграждения, а также группового времени запаздывания в полосе пропускания для ФНЧ Баттерворта.

 

Введем обозначения:

A_min – требуемое затухание фильтра в полосе заграждения;

A_max – требуемое затухание (допустимая неравномерность) фильтра в полосе пропускания;

Ω – текучая частота;

Ω_z – нормированная частота среза (отношение граничной частоты полосы заграждения к граничной частоте полосы пропускания);

Н_Аb(Ω) – амплитудно-частотная характеристика ФНЧ;

L_Аb(Ω) – рабочие затухание ФНЧ;

β_b (Ω) – фазо-частотная характеристика ФНЧ;

τ_b(Ω) – групповое время запаздывания;

 

Пусть заданы значения:

A_max : ≤ 2; A_min : ≥ 20 ; Ω_z : = 1.6;

 

Задаем пределы изменения и шаг изменения текущей частоты:

Ω : = 0.2 * Ωz/100 … 2 * Ωz

 

Wzcp – нормированная частота среза (fгрпн/fв)

Nb – порядок аналогового ФНЧ Баттерворта

Nc – порядок цифрового ФНЧ Чбышева

w – текущая частота

Hb(w) – АЧХ ФНЧ Баттерворта

Нс(w ) – ФЧХ ФНЧ Чебышева

τb(w) – групповое время запаздывания ФНЧ Баттерворта

τс(w) – групповое время запаздывания ФНЧ Чебышева

Amin1 – требуемое рабочее ослабление на частоте среза для фильтра Баттерворта

Amin2 – требуемое рабочее ослабление на частоте среза для фильтра Чебышева

Amax1 и Amax2 – допустимые неравномерности в полосе пропускания фильтров Баттерворта и Чебышева

 

Задание начальных данных

 

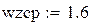
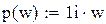
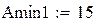
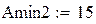
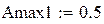
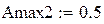
Допустимые значения группового времени запаздывания (ГВЗ) ФНЧ для аудиосогналов (из норм для трактов звукового вещания)

 

Fb – верхняя частота в спектре звукового сигнала

Amin – рабочее затухание на частоте среза (граничная частота полосы заграждения)

Amax – неравномерность в полосе пропускания

Допустимая неравномерность группового времени запаздывания τd(w)

 

Fb:=10000

 

w1	40/ Fb = 4×10-3	τd(w1)	55 мс
w2	75/ Fb = 7,5×10-3	τd(w2)	24 мс
w3	100/ Fb = 0,01	τd(w3)	20 мс
w4	6400/ Fb = 0,64	τd(w4)	5 мс
w5	7000/ Fb = 0,7	τd(w5)	10 мс
w6	14000/ Fb = 1,4	τd(w6)	8 мс
w7	15000/ Fb = 1,5	τd(w7)	12 мс

 

 

 

 

 

 

 

 

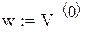
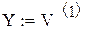
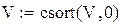
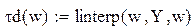
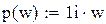
Рис. 6.53 Нормы на ГВЗ

 

Запишем выражения, необходимые для определения τb(w). Сначала определяется минимально необходимый порядок фильтра, удовлетворяющий заданным параметрам.

 

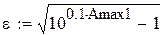
То есть требуется ФНЧ Баттерворта 6-го порядка. Далее следует определить наибольший порядок фильтра, удовлетворяющий требованиям по групповой задержке.

 

 

 

 

 

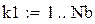
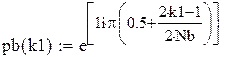
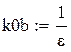
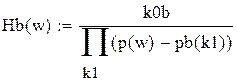
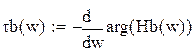
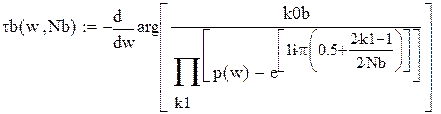
Запишем функцию цели для нахождения максимального порядка ФНЧ, удовлетворяющего требованиям по τ. Нормированные частоты выбраны 0,64 (по минимально допустимому значению групповой задержки) и 1 (соответствет Fb). Будем искать минимум функции цели, при котором задержка не превышает допустимого значения.

 

 

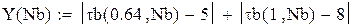
Введем пределы варьируемых параметров с помощью ключевого слова Given:

 

 

 

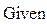
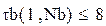
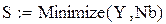
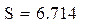
Поскольку N – целое число и N может быть меньше 6 для удовлетворения требований по затуханию чем меньше N, тем меньше получается значение τb , то принимаем N=6 и производим проверку на требуемых частотах:

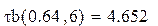
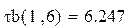
Таким образом, допустимо использование ФНЧ Баттерворта порядка 7, а требуется Nb=6. Следовательно, для Фнч Баттерворта следует принять порядок фильтра равным 6.

Определим теперь требуемый порядок ФНЧ Чебышева:

 

 

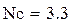
То есть требуется ФНЧ Чебышева 4-го порядка. Для него произведем проверку получаемого времени задержки на нормированных частотах 0.64 и 1.

Задание начальных значений параметров

 

 

 

 

 

 

 

 

 

 

 

 

 

 

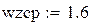
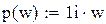
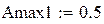
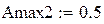
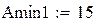
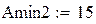
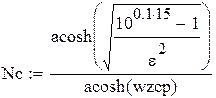
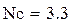
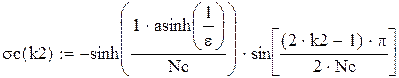
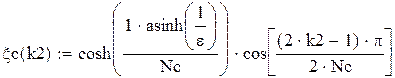
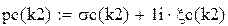
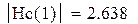
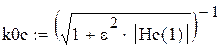
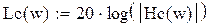
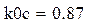
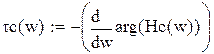
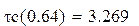
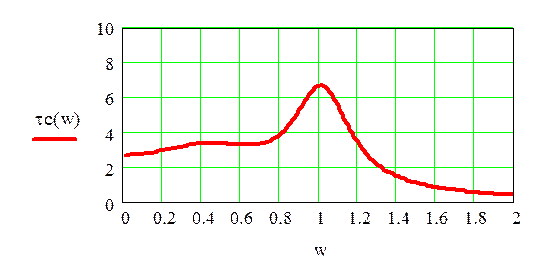
Рис 6.54 Групповое время запаздывания (в мс )

 

Таким образом ФНЧ Чебышева 4-го порядка удовлетворяет всем предъявляемым требованиям.

 

 

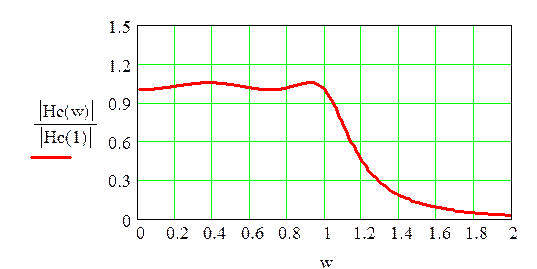
Рис. 6.55 АЧХ ФНЧ Чебышева 4-го порядка

 

 

 

 

 

 

 

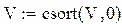
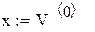
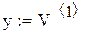
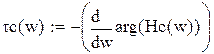
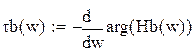
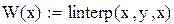
Рис 6.56 Зависимости допустимой и полученных групповых задержек

 

Вопросы для самоконтроля

 

1. Понятие оптимизациив расчетах РЭА

2. Понятие функции цели

3. Меры расхождения при определении функции цели

4. Методы поиска экстремума функции цели

5. Пример записи функции цели при синтезе фильтров

 

Анимация графического материала в среде MathCAD

Начиная с версии MathCAD–2000 появилась возможность «оживления» графических материалов. Для этого в MathCAD привлечена стандартная технология… Принцип, лежащий в основе «оживления» графиков, очень простой. В MathCAD… Диапазон переменной FRAME задается в диалоговом окне, которое появляется после запуска команды Record Animation…

Подготовка к анимации

Для построения анимационного графика в начале задается параметр FRAME как ранжированная переменная. Затем, записывается функция, которую надо «оживить» и у которой переменная FRAME должна определять ее вид для каждого кадра.

После этого в диалоговом окне «Record Animate» задаются три основных параметра: начальные значении переменной FRAME, ее конечное значение и частота смены кадров.

 

Пример анимации графика

1 Создаем системную переменную FRAME ранжированную переменную:

l:= FRAME·0.05

 

2 Задаем функцию, одним из параметров которой будет заданная на каждом шаге анимации переменная FRAME. Например, функция:

 

 

3 Выводим шаблон построение графиков в полярной системе координат.

4 В полях ввода шаблона вставляем имя функции и угол.

5 С помощью команды Record Animation выводим диалоговое окно «Запись анимации» для задания параметров анимации, рис. 6.57.

 

Рис 6.57 Диалоговое окно «Запись анимации»

 

6 Выделяем мышью нужный фрагмент изображения (графики и даже расположенные около него объекты, если нужно).

 

Для создания кадров изображения нажимаем указателем мыши на кнопке Animate (Анимация) окна параметров анимации. Это приводит к созданию последовательности анимационных кадров, что будет видно в области просмотрового окна.

С помощью кнопки Options (Установки) можно выбрать формат сжатия видео файлов и систему работы с ними. Чем больше конечное значение переменной FRAME и выше частота кадров, тем более плавно происходит считывание.

По окончании создания серии кадров для анимации появится окно проигрывателя «Play Animation» (Просмотр анимации), рис. 6.58

 

 

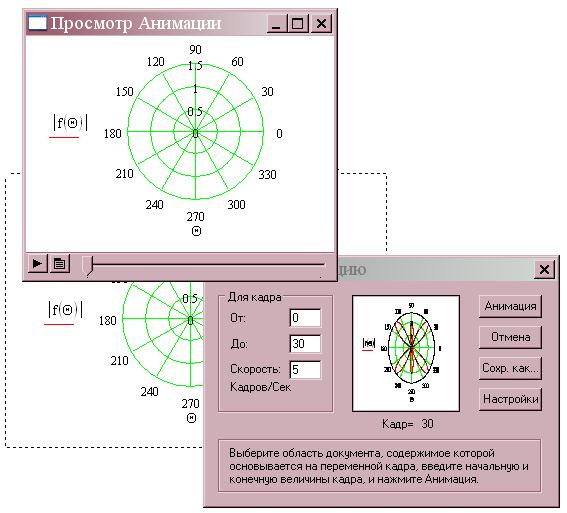
Рис 6.58 Окно проигрывателя «Play Animation» (Просмотр анимации)

 

Теперь можно приступить к просмотру клипа. Для просмотра необходимо щелкнуть в окне проигрывателя на кнопку с изображение треугольник. После этого в окне проигрывателя начнется воспроизведение графика во времени.

Если щелкнуть на кнопке Save As (сохранить как) в диалоговом окне Record Animation, то появится стандартное окно записи файлов на диск. С помощью этого окна файл будет записан в нужную папку с расширением *.avi. Размеры окна проигрывателя можно уменьшать или увеличивать в 2 раза. Это делается с помощью меню, появляющегося в окне проигрывателя после щелчка на кнопке с изображением экрана.

 

Вызов проигрывателя анимации графиков и видео файлов

Любой файл с расширением *.avi может быть просмотрен с помощью проигрывателя, запускаемого командой PlayBack (Проиграть) меню Tools (Инструменты),… После появления окна проигрывателя Play Animation необходимо загрузить в…  

Установка связи MathCAD с другими программными средами

Возможности MathCAD в подготовке текстовых документов, электронных таблиц, динамических программных объектов, построения иллюстративной графики и… Установка связей с внешними программными продуктами выполняется из меню Insert…  

Обзор инструкций

2 «←» − символ локального присваивания (в теле модуля или блока); 3 if (если) − условная инструкция; 4 for (для) − инструкция задания цикла с фиксированным числом повторения;

Инструкция Add line

Инструкция «Add Line» ( добавить линию) выполняет функции создания и расширения программного блока. Расширение фиксируется удлинением вертикальной черты программных блоков или их древовидным расширением. Благодаря этому можно создавать сколь угодно большие программы.

 

Оператор внутреннего присваивания

Для присвоения значений переменным, выражениям и константам в программах «MathCAD» используется специальный оператор «←» (локальное определение), расположенный на панели «Программирование», он также вводится сочетанием клавиш «Shift» + «[». Использовать оператор обычного присвоения «: = » в программах нельзя.

Оператор «←» выполняет функции внутреннего, локального присваивания. Например, выражение х ← 123 присваивает переменной х значение 123.

Локальный характер присваивания означает, что такое значение переменной х хранится только в теле программы. За пределами тела программы значение переменной х может быть неопределенным либо равным значению, которое задается вне программного блока операторами локального « := » или глобального « ≡ » присваивания.

 

 

7.1.3 Условная инструкция «if»

Инструкция «if» (если) позволяет строить условные выражения. Она задается в виде: «выражение» if «условие». Если условие выполняется, то возвращается (определяется) значение «выражения». Совместно с этой инструкцией часто используются инструкции прерывания «break» и иного выбора «otherwise».

 

7.1.4 Инструкция «for»

Данная инструкция служит для организации циклов с заданным числом повторений. Она записывается в виде:

 

for Var 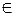N_min .. N_max

 

Эта запись означает, что выражение, помещённое в расположенное ниже место ввода, будет выполнятся для значений Var, меняющихся от N_min до N_max с шагом +1. Переменную Var можно использовать в исполняемом выражении.

 

7.1.5 Инструкция «while»

Инструкция служит для организации циклов, действующих до тех пор, пока выполняется некоторое условие.

Она записывается в виде:

 

while «условие»

 

Выполняемое выражение записывается в расположенное ниже место ввода.

7.1.6 Инструкция «otherwise»

 

Инструкция иного выбора «otherwise» обычно используется совместно с инструкцией «if» (если). Это поясняет следующая программная конструкция:

 

 

 

То есть функция f(x) возвращает 1, если х > 0, и -1 во всех остальных случаях.

7.1.7 Инструкция «break»

 

Инструкция «break» вызывает прерывание выполнения программы всякий раз, как она встречается.

Чаще всего эта инструкция используется совместно с условной инструкцией «if» (если) и инструкциями циклов «while» (пока) и «for» (для), обеспечивая перехода в конец тела цикла.

 

7.1.8 Инструкция «continue»

Инструкция «continue» (продолжение) используется для продолжения работы после прерывания программы.

Она чаще всего используется совместно с инструкциями циклов «while» и «for», обеспечивая возвращение в точку прерывания и продолжение вычислений.

 

7.1.9 Инструкция «return»

Эта инструкция прерывает выполнение программы и возвращает значение операнда, стоящего следом за ней. Например, в приведенном ниже случае будет возвращаться значение 0 при х<0:

return 0 if х<0

7.1.10 Инструкция «on error»

 

Эта инструкция позволяет создать процедуры обработки ошибок. Она задается в виде:

«выражение 1on error выражение 2»

Если при выполнении выражения 1 возникла ошибка, то выполняется выражение 2.

 

Создание программ

Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения алгоритма. Для того, чтобы построить единичный элемент программного блока, следует нажать… В области курсора появится следующий объект:

Особенность присвоения значения функции

  Пример:

Общие принципы задания операторов

1) Что бы задать нужный оператор, необходимо использовать соответствующие команды панели «программирование».

Просто набрать оператор с клавиатуры нельзя ─ он будет воспринят системой как неизвестная функция.

Кроме того, каждый оператор программирования имеет свое сочетание «горячих клавиш», узнать которое можно, подведя курсор к соответствующей ему кнопке рабочей панели.

2) Задание комплекса условий в программных операторах можно делать по разному:

─ Можно поставить курсор в соответствующий маркер оператора, задействовать команду «Add Line» (добавить линию). В появившемся программном блоке определить условия. При таком задании условий оператор будет выполнен, если будет выполнено хотя бы одно условие из множества условий (что соответствует использованию логического оператора «или»).

─ В том случае, если оператор должен быть задействован при условии выполнения всего комплекса условий, следует использовать логическое умножение «И» панели «булевы».

 

Примеры составления программ

Пример задания комплекса условий

 

Пусть требуется вычислить сумму гармонического ряда из произвольного числа членов n. Условия суммирования ─ сумма не должна превысить 10.

Суммирование будем осуществлять с использованием оператора условного цикла «While» (пока).

Принцип его работы следующий:

если выполняется условие в его правом маркере, то выполняются и выражения в левом.

Можно записать программу следующим образом:

 

 

 

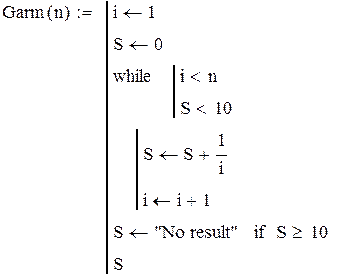
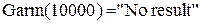
Очевидно, что программа работает некорректно.

Произведем суммирование с помощью специального оператора:

 

 

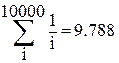
Ошибка в программе связанна с тем, что записана связь условий подобно логическому «ИЛИ».

Это заставляет оператор работать, пока выполняется хотя бы одно условие.

Поэтому суммирование будет производится до тех пор, пока результат не достигнет 10 (при этом будет просуммировано 12370 элементов вместо необходимых 10000).

Запишем программу, используя для связи условий логическое «И». В этом случае для продолжения цикла «while» требуется, чтобы исполнялись оба условия. Когда число членов суммы достигнет n, одно из условий перестанет выполнятся, цикл останавливается и выдается верный ответ.

 

 

 

 

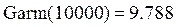
Таким образом видно, что правильно работает программа, в которой комплекс условий записан через логический оператор.

Во втором случае, когда число членов достигает 10000 (т.е. заданного n), одно из условий перестает выполнятся, цикл останавливается и выдается верный ответ.

 

Пример расчета с заданной точностью

 

Рассмотрим программу подсчета суммы сходящегося ряда с заданной точностью, которая имеет ряд важных технических особенностей.

 

 

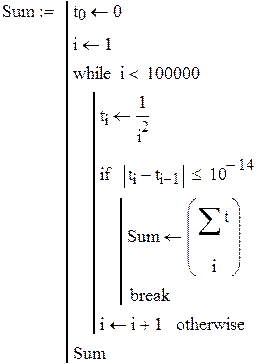
Проверку можно сделать с помощью оператора суммирования:

 

 

Разберем создание программы по пунктам.

 

1) Сначала вводим имя программы и блок из нескольких маркеров.

2) Задаем условный цикл «While» (пока). В качестве условия остановки в его правом маркере определим, что число операций суммирования не должно превышать 100000.

Это необходимо в связи с тем, что если ряд не сходится или сходится очень медленно, то подсчет может вестись неограниченно долго.

 

 

3) Затем задаем вид общего члена ряда:

 

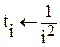
Он определится как элемент вектора: это нужно для того, что бы затем была возможность подсчитать максимально просто сумму всех членов ряда.

4) Далее определяется условие остановки цикла. Делается это при помощи условного оператора «if». В качестве условия задано, что два соседних члена ряда должны отличаться по абсолютной величине не более, чем на 10^-14 (такой подход возможен только в случае равномерной сходимости).

5 Определяется первый элемент вектора t₀ как 0:

 

 

Иначе возникает проблема: с чем будет сравниваться первый член ряда.

6) В левом маркере условного оператора цикла (на самом деле он выводится ниже оператора) задаются те операции, которые должны быть произведены при выполнении условия точности.

Так как их несколько, то вводим дополнительный программный блок.

Во-первых, требуется произвести суммирование рассчитанных членов ряда. Так как они были сохранены в форме вектора, то операцию суммирования следует выполнить при помощи специального оператора суммы элементов вектора (Vector Sum) панели «матрица»:

Во-вторых, интересно узнать, сколько просуммировано элементов. А так как в качестве результата работы программы может быть выведен только один объект, то интересующие величины следует объединить в один вектор:

 

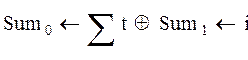
Для объединения операций в данном случае пришлось использовать оператор исключающего «или». При использовании логического «ИЛИ» ответ был бы выведен неполным: в нем бы присутствовало только значение суммы, и не было бы числа членов ряда.

Проще можно было бы объединение в один вектор произвести его непосредственным определением:

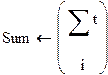
Так как задача программы выполнена, цикл должен быть остановлен. Делается это с помощью специального оператора остановки «Break». Он почти всегда используется с оператором «if».

7) В том случае, если условие точности выполнено не было, цикл должен продолжить свою работу. Однако на следующем круге должен быть рассмотрен уже следующий член ряда. Для этого следует увеличить значение переменной на 1:

 

 

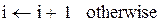
Подобное переопределение переменной (или функции) через саму себя называется реккурентным.

Несмотря на то, что с точки зрения математики реккурентные выражения выглядят алогично, они являются одним из наиболее мощных и широко используемых средств компьютерной математики.

Первое значение переменной i (индекса) должно быть задано выше цикла как 1.

8) В конце первой программной линии вводим имя той величины, которая должна быть выдана в качестве ответа. В нашем случае это вектор «Sum».

Необходимо помнить, что в качестве результата работы программы выводится значение того выражения, которое находится в последнем маркере главного программного блока.

Ошибившись с его определением (или забыв задать его вовсе), можно получить совсем не тот ответ, который соответствует решению данной задачи.

 

Пример расчета различных параметров одной и той же программой

 

 

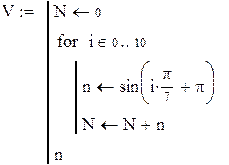
Создание новых функций с помощью программирования

Любая программа может быть задана как функция. Причем параметры ее могут быть определены в общем виде. Подставив в маркеры, созданной таким образом функции, какие-то числовые… Такой подход позволяет значительно экономить время в том случае, если программа должна быть использована много раз. …

Поиск ошибок в программах

В MathCAD подобной процедуры нет, однако возможность быстро и легко определять ошибки в синтаксисе алгоритма имеется. Рассмотрим ошибочную ситуацию: при попытке использования программы,…  

Листинг программы расчета ФНЧ Чебышева

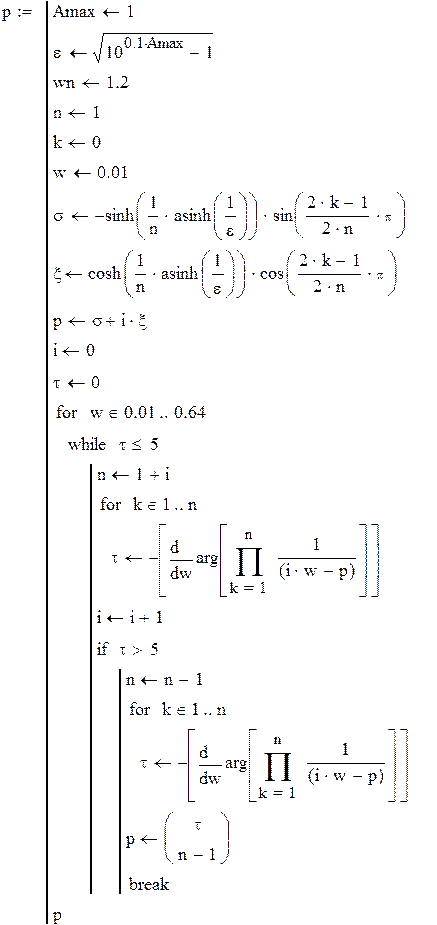
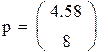
Листинг программы расчета фильтра Баттерворта по критерию ограничения во времени группового запаздывания

 

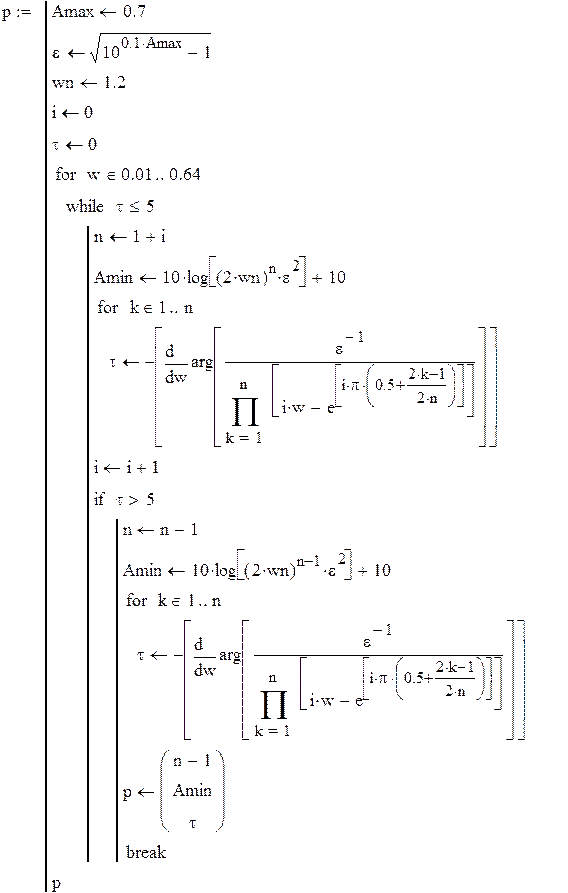
Глава 8. ОЦЕНКА ИСКАЖЕНИЙ СИГНАЛОВ ПРИ ПРОХОЖДЕНИИ ЧЕРЕЗ НЕЛИНЕЙНЫЕ УСТРОЙСТВА

В большинстве случаев нелинейным элементом в радиотехнических устройствах являются электронные приборы. В сочетании с инерционными электрическими цепями они образуют нелинейные динамические звенья и устройства.

Математическая модель таких устройств может быть представлена в виде системы из n нелинейных дифференциальных уравнений.

В [9] рассмотрены применяемые в радиотехнике методы решения таких уравнений (аналитические, численные, реализуемые только с помощью компьютера).

В данном разделе рассматривается применение квазистационарного метода расчета спектра на выходе таких нелинейных устройств как ограничитель и компрессор, что актуально для большинства усилительных трактов.

В приложении к обработке аудиосигналов подобные задачи встречаются в звуковом вещании, при записи и воспроизведении аудиосигналов, в задачах аналого-цифрового преобразователя.

 

Оценка нелинейных искажений при компресии и ограничении аудиосигналов на входе цифровых трактов

Ниже приводится сравнительная оценка искажений, возникающих при безынерционном ограничении и компрессии верхней части динамического диапазона… Оценка проведена для одночастотного периодического сигнала методом… Введены обозначения:

Ограничитель (пикосрезатель) Компрессор

  Амплитуда входного сигнала в dB:

Вопросы для самоконтроля

1. Какой метод расчета спектра на выходе нелинейных устройств рассмотрен в комплексе?

2. Оценка каких искажений и каким методом проведена в разделе 8?

 

Глава 9. ЦИФРОВАЯ ФИЛЬТРАЦИЯ

 

В общем случае под фразой цифровая фильтрация нужно понимать любое преобразование над дискретным сигналом, а не только выделение сигнала определенной полосы частот. В этом смысле понятие «цифровой фильтрации» и «дискретная система» - это одно и тоже. Однако, в этом разделе речь пойдет именно о цифровых фильтрах, т.е. устройствах работающих с дискретными сигналами и выделяющих определенный спектр.

Помимо очевидных преимуществ устранения ошибок в фильтре стабильности характеристик, и т.д., цифровые фильтры позволяют получить такие технические характеристики, которые трудно или даже невозможно получить в аналоговых фильтрах. Кроме того, характеристики ЦФ могут быть легко изменены программно. Сами фильтры могут быть реализованы либо в виде программного продукта, либо с использованием специализированных БИС или цифровых сигнальных процессоров.

Процесс проектирования ЦФ состоит их тех же этапов, что и проектирование аналоговых фильтров. Вначале формулируются требования к желаемым характеристикам фильтра, по которым затем рассчитываются параметры фильтра. Амплитудная и фазовая характеристики формируются аналогично аналоговым фильтрам.

В задачу проектирования ЦФ так же входит выбор подходящей структуры реализации дискретного фильтра с учетом точности вычислений. Основное различие между ЦФ и АФ состоит в том, что вместо вычисления сопротивлений, емкостей и индуктивностей в аналоговых системах, рассчитываются значения коэффициентов. Эти коэффициенты {a_i}, {b_i} являются аналогами физических сопротивлений, емкостей и индуктивностей АФ. Их и необходимо найти в первую очередь при синтезе ЦФ

Дискретная система, как и аналоговая, полностью может быть описана математическим оператором, устанавливающим связь между выходным и входным сигналами или последовательностями [1]:

 

y(i) = F(x(i)) (9.1)

 

Оператор системы, реализуется аппаратными или программными средствами, и называется алгоритмом обработки системы.

В случае одномерной цифровой фильтрации последовательность отсчетов x(i) входного сигнала преобразуется в последовательность отсчетов выходного сигнала y(i) по общей формуле:

 

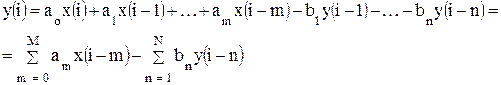(9.2)

 

Значения m и n могут быть любыми натуральными числами, а коэффициенты a_i, b_i могут быть любыми действительными числами (положительными и отрицательными). M ≥ N обозначает порядок уравнения. Устройство или программу, реализующие разностное уравнение (9.2) и называют дискретным или цифровым фильтром.

Сигнал на выходе ЦФ равен сумме текущего отсчета входного сигнала и предыдущих (N и M) отсчетов входного и выходного сигналов взятых с весовыми коэффициентами a_i, b_i.

Рис. 9.1 Представление дискретного сигнала

 

Если хотя бы один из коэффициентов b_i не равен нулю, ЦФ называется рекурсивным, [2]. Рекурсия означает наличие в фильтре обратных связей, и текущее значение выходного сигнала будет определяться не только входным сигналом, но и более ранними значениями выходного сигнала y(i – n), (рис. 9.1). Такие фильтры еще называют фильтрами с бесконечной импульсной характеристикой (БИХ – фильтры), так как они «помнят» все предыдущие значения входного и выходного сигналов и их импульсная характеристика бесконечна (рис. 9.2).

РФ позволяют производить обработку сигнала с высокой точностью, так как у них импульсная характеристика не усекается, позволяют организовать алгоритмы обработки сигналов практически любой сложности, простая схемная реализация, т.е. содержат относительно небольшое число элементов. Однако, из-за наличия обратных связей такие фильтры склонны к самовозбуждению, а их фазовая характеристика в общем случае нелинейная.

 

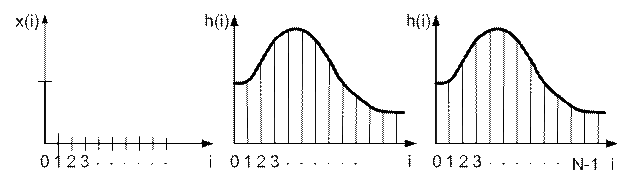а) б) в)

 

Рис. 9.2 Единичный входной импульс (а) и импульсные характеристики: БИХ – фильтра (б) и КИХ – фильтра (в)

 

Если все коэффициенты b_i=0 , то уравнение (9.2) преобразуется к виду:

 

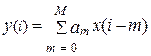, (9.3)

 

тогда ЦФ называется нерекурсивным. Его импульсная характеристика становится конечной и фильтр называется фильтром с конечной импульсной характеристикой (КИХ – фильтр) (рис. 9.2, в).

Дискретная временная свертка для НФ имеет конечные пределы суммирования, определяемые конечной длиной импульсной характеристики фильтра N:

(9.4)

Сравнивая выражения (9.3) и (9.4) видно, что дискретная временная свертка (ДВС) может непосредственно использоваться при реализации алгоритма обработки в НФ, и отсчеты импульсной характеристики являются коэффициентами фильтра.

НФ имеют почти линейную ФЧХ, мощность собственных шумов, как правило, меньше чем у РФ, проще вычисление коэффициентов, всегда устойчивы и просты в настройке. Однако НФ содержат большое число элементов цепи и не позволяют производить обработку дискретных сигналов с высокой точностью.

Устойчивость ЦФ можно оценить по импульсной характеристике. Для устойчивого ЦФ импульсная характеристика затухает со временем, что математически 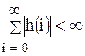. Обобщенная структурная схема ЦФ имеющего как рекурсивную, так и нерекурсивную части показаны на рис. 9.3.

 

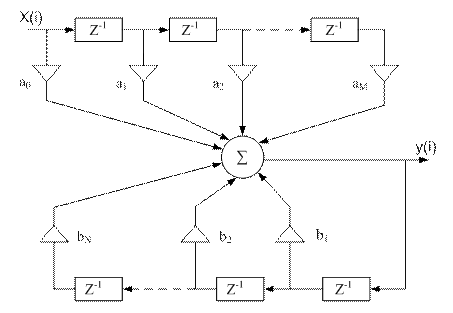
Рис. 9.3 Обобщенная структурная схема ЦФ

 

Здесь блоки Z^-1 выполняют роль линии задержки сигнала на один отсчет (Т = 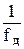). Операционные усилители определяют коэффициенты фильтра.

 

Рекурсивные цифровые фильтры

Рекурсивный фильтр реализует алгоритмы обработки входного сигнала, описываемый уравнением (9.2). Применяя Z-преобразования к левой и правой части…   ,

Формы реализации рекурсивных фильтров

Рекурсивные фильтры осуществляют обработку сигналов в соответствии с разностным уравнением и основными формами реализации фильтров являются: прямая… РФ порядка выше второго (по числу полюсов N) реализуется, чаще всего, путем…  

Методика синтеза РФ по аналоговому прототипу

Синтез передаточной функции H(z) по заданной частотной характеристике Hd(jω) заключается в ее аппроксимации и определении коэффициентов… Аналитические методы обеспечивают решение задачи аппроксимации в замкнутой… Итерационные методы, сочетая аналитический и численный подходы, не дают однозначного соответствия параметров расчетных…

Синтез аналогового фильтра прототипа

Синтез АФПНЧ включает выбор аппроксимирующей функции, определение порядка фильтра N, значений нулей pоi и полюсов ppi передаточной функции по…  

Расчет числа звеньев и определение полюсов и нулей низкочастотного фильтра прототипа

 

Фильтр Баттерворта

   

Фильтр Чебышева

  an = 10lg(1 + ε2) , [дБ]  

Фильтр Чебышева инверсный

  Здесь ω0 – частота среза фильтра; Tn– полином Чебышева n-ого порядка;

Эллиптический или фильтр Кауэра

Функция передачи имеет как полюсы, так и нули. Нули, как и в случае Чебышева второго рода, являются чисто мнимыми и образуют комплексно-сопряженные… Для определения числа звеньев в фильтре необходимо определить ряд… Здесь ε – параметр определяющий пульсацию в полосе пропускания an = 10lg(1 + ε2); k и k1 – модули полных…

Переход от аналогового фильтра прототипа к цифровому фильтру

С помощью обобщенной преобразующей функции (см. формулу (9.15)) передаточную функцию низкочастотного прототипа можно непосредственно… Однако такой путь связан с громоздкими математическими преобразованиями,… Более удобный путь основан на аналитической связи между коэффициентами ЦФ конкретной формы реализации и его нулями и…

Порядок и пример синтеза цифрового рекурсивного фильтра

 

В общем виде порядок синтеза РЦФ можно представить так:

· с помощью частотных преобразований (таблица 9.1) по заданным значениям граничных частот ЦФ: ω_с, ω_з (Ω_с, Ω_з) находятся граничные частоты аналогового фильтра прототипа (ω_aс= 1, ω_aз);

· по значениям a_n , a_з , и ω_aз синтезируется фильтр прототип: выбирается тип аппроксимирующей функции, определяется порядок фильтра N и значения его полюсов и нулей: ω_aоi, ω_api, i = 1, 2, … , N;

· по формулам таблицы 9.2 рассчитываются значения полюсов и нулей ЦФ заданного типа: z_оi , z_рi , i = 1, 2, … , N, (здесь N – порядок ЦФ и для ФНЧ, ФВЧ, а для ППФ и ПЗФ 2·N);

· Порядок фильтра равен порядку АФП.

· строится картина расположения нулей и полюсов ЦФ на комплексной плоскости; каждому i-му звену ЦФ ставится в соответствие комплексно-сопряженная или вещественная пара полюсов, а в случае каскадной формы реализаций – ближайшая к ней по расположению пара конечных нулей (i = 1, 2, … , L);

· выбирается форма (структура) реализации РФ и рассчитываются коэффициенты звеньев фильтра a_1i, a_2i, b_оi, b_1i, b_2i по соотношениям рассмотренным выше;

· рассчитывается АЧХ и ФЧХ фильтра и сопоставляются с заданными требованиями.

В случае если синтезированный фильтр не удовлетворяет поставленным требованиям, расчеты повторяются до получения нужного результата.

Ниже приведен пакет программного модуля, написанный в среде MathCAD, по синтезу полосового рекурсивного фильтра, для всех вариантов аппроксимирующих функций рассмотренных ранее.

Исходные данные: полосовой фильтр с полосой пропускания 8400 ÷ 11600 (Гц), полосой задерживания 7600 ÷ 12400 (Гц), неравномерностью в ПП a_n = 1[дБ], затуханием в ПНП a_з = 40[дБ] и частотной дискретизацией f_д = 112000 (Гц).

 

Текст программного модуля синтезирующего цифровой рекурсивный ППФ

0 Данные для проектирования:  

Максимальная апроксимация

     

Чебышевская апрксимация

Расчет числа звеньев и определение полюсов и нулей НЧФП    

Инверсия Чебышевская аппроксимация

     

Эллиптическая аппроксимация

Расчет эллиптических интегралов, эллиптических функций, числа звеньев и определение полюсов и нулей НЧФП :    

Синтез нерекурсивных фильтров

Синтез нерекурсивных фильтров методом весовых функций

В данном случае синтез фильтра осуществляется с помощью весовых функций (или с помощью взвешивающих окон), является универсальным методом, что… Частотная характеристика и импульсная связаны парой преобразований Фурье.…  

Основные параметры весовых функций

  Таблица 9.3   № Тип Δωгл абmax, дБ Прямоугольная …

Импульсные характеристики идеальных ЦФ различного типа

Аналитические описания импульсных характеристик ЦФ различного типа получаются в общем случае путем выполнения обратного преобразования Фурье их… Для идеального цифрового ФНЧ импульсная характеристика определяется…  

Методика синтеза НФ методом весовых функций и пример синтеза полосового цифрового фильтра

 

Подводя итог выше сказанному, приведем общую методику синтеза НФ.

По заданному значению затухания частотной характеристики в полосе задерживания а_з с помощью таблицы 9.3 выбирается тип весовой функции, отвечающей условию 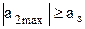, при минимальном значении ширины ее главного лепестка, т.е параметра D. При использовании весовой функции Кайзера по таблице 9.4 находятся соответствующие заданному затуханию а_з параметры данной весовой функции β и D. При этом нужно учитывать, что расчетное значение затухания зависит от вида АЧХ синтезируемого фильтра, его граничных частот и длины весовой функции N и может оказаться как больше, так и меньше оценочного значения а_2max. Чем сложнее АЧХ фильтра (ППФ, ПЗФ, МПФ), тем меньше затухание для одной и той же весовой функции. Это же относится и к неравномерности АЧХ в полосе пропускания.

Для выбранной весовой функции и заданной переходной полосы частотной характеристики фильтра 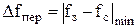в соответствии с приближенным соотношением 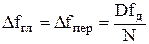находится необходимая длина весовой функции и определяемая ею длина импульсной характеристики фильтра: 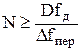, где D – коэффициент зависящий от типа весовой функции.

Значение N приравнивается ближайшему целому нечетному числу.

С помощью обратного преобразования Фурье:

 

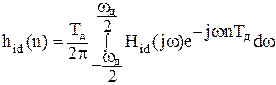
или приведенных выше аналитических выражений вычисляется смещенная вправо импульсная характеристика 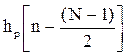, n = 0, . . ., N – 1, соответствующая заданной частотной характеристике H_p(jω).

При этом в качестве частот среза заданной частотной характеристики используют их расчетные значения f_ср, смещенные в полосу задерживания примерно на половину переходной полосы фильтра Δf_пер. Это связано со свойственным данному методу размыванием границ перехода от полосы пропускания фильтра к полосе задерживания (рис. 9.31).

Например, для ППФ:

 

;

 

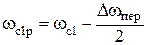Находится импульсная характеристика фильтра путем весового усечения смещенной вправо на 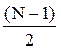отсчетов импульсной характеристики h_p(n):

 

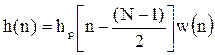, n = 0, . . ., N – 1

 

Рассчитывается АЧХ фильтра 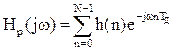и проверяется ее соответствие исходным данным по неравномерности частотной характеристики в полосе пропускания а_п и затуханию в полосе задерживания а_з.

Так как данный метод не обеспечивает точного соответствия исходных и расчетных данных (является итерационным), при необходимости корректируются значения расчетных частот среза ω_с1р, ω_с2р , длины фильтра N и расчеты повторяются.

Выбирается способ реализации НФ (на основе ДВС, ДПФ или частотной выборки) и решаются соответствующие ему задачи реализации.

Следует отметить, что метод весовых функций обеспечивает строгую линейность ФЧХ и постоянство группового времени запаздывания фильтра ввиду четной или нечетной симметрии получаемой этим методом импульсной характеристики h(n).

Далее приводится листинг программы, написанной в среде MathCAD, по синтезу НФ методом весовых функций.

Текст программного модуля синтезирующего цифровой нерекурсивный ППФ методом ВФ

0 Данные для проектирования  

Окно прямоугольное № 1

     

Окно Бартлетта № 2

     

Окно Ханна № 3

     

Окно Хемминга № 4

     

Окно Блекмена № 5

     

Окно Кайзера № 6

     

Окно Карре 2-ое № 7

     

Окно Лапласа-Гауса № 8

     

Окно Ланцоша № 9

   

Окно Чебышева № 10

t:=0..N    

Синтез нерекурсивного фильтра методом частотной выборки

В методе частотной выборки импульсная характеристика фильтра h(n) находится путем дискретизации по частоте заданной частотной характеристики… Дискретизация частотной характеристики Hid(jω) по частоте осуществляется… Шаг дискретизации по частоте Δω выбирается из условия , где L – целые числа, L = 0, 1, 2, . . .;…

Методика синтеза НФ методом частотной выборки

По значению заданного затухания в полосе задерживания аз выбирается число варьируемых отсчетов частотной характеристики в переходной полосе L.… Для принятого значения L и заданной переходной полосы находим шаг… Дискретизируем заданную частотную характеристику Hid(jω) с шагом Δf, в результате чего получаем ДЧХ…

Текст программного модуля синтезирующего цифровой нерекурсивный ППФ методом ЧВ

0 Данные для проектирования  

Активный RC-фильтры

В активных фильтрах с обратными связями, используются параллельные и другие виды соединений четырехполюсников. Четырехполюсник, по которому сигнал…  

Передаточные функции фильтров

В общем виде алгоритм синтеза ARC- фильтров сводится к следующему: · формируются требования к его амплитудной частотной характеристике (АЧХ),… · по требованиям к АЧХ синтезируется передаточная функция фильтра в виде произведения функций не выше 2-го порядка; …

Преобразование частот

АЧХ ФПНЧ определена на нормированной оси частот так, что граничная частота ПП Ωn = 1, а граничная частота полосы задерживания Ωn>1. В… Для ППФ и ПЗФ – центральная частота полосы пропускания ω0 = . Формулы для…  

Реализация звеньев первого порядка

Передаточная функция фильтра нижних частот первого порядка в общем случае определяется выражением (9.22). Фильтр с такой передаточной функцией может…  

Реализация звеньев второго порядка

В общем виде выражение передаточной функции ФНЧ второго порядка для фильтров полиноминального типа можно записать так: (9.27)  

Текст программного модуля расчета нч arc-фильтра

   

Глава 10. СИНТЕЗ ЛИНЕЙНЫХ АНТЕННЫХ СИСТЕМ

 

В этой главе будут рассматриваться простейшие линейные излучающие системы. Под линейной излучающей системой будет пониматься непрерывное или дискретное распределение одинаковых источников электромагнитного поля (т.е. излучателей), вдоль заданного направления в пространстве (рис.10.1). Примерами таких излучателей могут быть: длинный прямолинейный провод, щели в экране или в стенках волновода, диэлектрический стержень, система одинаковых излучателей (напр. вибраторов), спиральная антенна и т.д. Продольный размер излучателя может быть произвольным, а поперечные размеры, как правило, меньше длины волны. Как правило, комплексная характеристика направленности одного элемента излучателя известна.

Рис.10.1 Линейные излучатели

Общая постановка задачи

Требуемая диаграмма направленности задается в виде известной комплексной функции и ищется функция распределения возбужденияв ограниченной объеме… (10.1) и добиваются ее минимума подбором соответствующего возбуждения. Такое приближение используют, когда направленные…

Характеристика направленности как целевая функция

(10.6)   Чтобы функция допускала преобразование (10.6), она должна интегрироваться с квадратом на интервале (-…

Синтез линейного излучателя методом парциальных диаграмм направленности

Пусть распределение возбуждения в линейном излучателе имеет вид , (10.8) ряда из некоторых известных функций . Подставим этот ряд в выражение для характеристики направленности антенны…

Синтез излучателей методом интеграла Фурье

(10.16) Однако, требуемая характеристика известна только в пределах действительных… Можно задаться конкретной длиной излучателя и методами теории функций комплексного переменного построить аналитическое…

Описание программ синтеза линейного излучателя в среде Mathcad

Рис.10.2 Требуемая ДН … Рис.10.3 Парциальная ДН

Синфазные антенные решетки с оптимальной диаграммой направленности

Диаграмма направленности синфазной решетки с симметричным, относительно ее середины, амплитудным распределением будет определяться выражением [2]: … при четном числе излучателей N, при нечетном числе излучателей N.

Расчет амплитудного распределения возбуждения в линейных антенных решетках

Рис.10.15

Программа синтез антенной решетки по заданному уровню боковых лепестков

  Определение параметра формы ДН (zo) и амплитуды токов в излучателях (Jg) . …   …  

Глава 11. О МОДЕЛИРОВАНИИ КАНАЛА СВЯЗИ

Применение метода малых отклонений при моделировании каналов

Развитие модельного эксперимента при разработке и исследованиях телекоммуникационных систем (ТС) обусловлено как сложностью моделирования систем,… В процессе модельного эксперимента обычно производится оценка… Для техники телекоммуникаций актуальным является передача и прием дискретных сообщений. Развитие теории и техники…

Определение погрешностей моделирования (оценки средней вероятности ошибки) методом малых отклонений

Рассматривается методика, позволяющая установить соответствие между погрешностями моделирования параметров стохастического канала и отличием средней… Поставленная задача решается расчетно-аналитическим методом, использующим… Допустим, что для рассматриваемой реализации модели канала средняя вероятность ошибки при исследовании СПДИ отличается…

Погрешности моделирования канала при исследованиях двоичных систем связи

Задача всех последующих разделов данной главы – получить аналитические соотношения между отклонениями моделируемых параметров и относительной… В данном параграфе рассматривается моделирование каналов с флуктуационными… В соответствии с терминологией [] гладкими (общими) замираниями будем называть такие изменения амплитуды и фазы…

Когерентный прием при моделировании релеевских замираний

Вероятность ошибок при когерентном приеме двоичных сигналов в условиях медленных релеевских замираний определяется путем усреднения условной… (11.13)

Прием сигналов относительной фазовой телеграфии при моделировании релеевских замираний

Средняя вероятность ошибки на приеме [] , (11.16) где – среднее значение отношения энергии сигнала к удельной мощности помехи на входе приемного устройства;

Литература

1. Б.Советов, С.Яковлев Моделирование систем. Учебник для вузов. «Питер» С-П. 602 с. 2005

2. А.Б. Сергиенко. Цифровая обработка сигналов. 2-е издание. Издательство Питер. 2007, 751с.

3. Хемминг Р.В. Цифровая фильтры.–М.: Недра, 1987.-221с.

4. Тронин Ю.В., Гурский О.В., Демин М.П. Дискретные сигналы и их обработка. – М.: МАИ, 1985.

5. А.Т. Бизин «Цифровая обработка сигналов». Учебное пособие / Сиб.ГОС.ун-т телекоммуникаций и информатики. – Новосибирск,2005 г. – 86 с.

6. А.С. Глинченко. Цифровая обработка сигналов. г.Красноярск 2001. учебное пособие.

7. Куприянов М.С., Матюшкин Б.Д. – Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. – СПб.: Политехника 1999

8. Минпазин А.Т. Синтез передаточных функций цифровых фильтров в области дискретных значений коэффициентов (обзор). // Электронная техника. Сер.10.1993.№1,2.С.3-35.

9. Зааль Р. Справочник по расчету фильтров/Пер.С:под ред. Н.Н. Слепови – M.:Р. и С., 1983

10. В.И.Каганов. Радиотехника + компьютер + MathCAD. – Ь.: горячая линия – Телеком, 2001.-416 с.

11. Выходец А.В., Гитлиц М.В. Радиовещание и электроника. – М.: Радио и связь, 1989. – 542 с.

12. Ковалгин Ю.А. Радиовещание и электроакустика. – М.: Радио и связь, 1999. –792 с.

13. Д.А. Гурский, Вычисления в MathCAD . – Минск.: новое знание. 2003. –814 с.