Повторение предыдущего материала
Лекция 5
Повторение предыдущего материала
Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна,… 2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на… (а, b), причем f ¢ (x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].Асимптоты.
Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность… Следует отметить, что не любая кривая имеет асимптоту. То есть асимптоты может и не быть.Схема исследования функций
Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
1) Область определения функции.
2) Точки разрыва. (Если они имеются). Если есть точки разрыва, то посмотреть нет ли вертикальных асимптот.
3) Наклонные асимптоты, если имеются.
4) Найти точки пересечения графика функции с осями координат. Определить промежутки знакопостоянства функции (т.е. промежутки, на которых функция сохраняет знак).
5) Найти производную 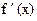 и критические точки. Определить знаки производной и найти интервалы возрастания и убывания. Определить точки максимума и минимума.
и критические точки. Определить знаки производной и найти интервалы возрастания и убывания. Определить точки максимума и минимума.
6) Найти вторую производную 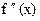 и критические точки второго рода (т.е. такие точки, в которых вторая производная равна нулю или не существует). Определить знаки второй производной и найти интервалы выпуклости и вогнутости. Определить точки перегиба.
и критические точки второго рода (т.е. такие точки, в которых вторая производная равна нулю или не существует). Определить знаки второй производной и найти интервалы выпуклости и вогнутости. Определить точки перегиба.
7) Построение графика.
Применение этой схемы рассмотрим на примере.
Пример. Исследовать функцию  и построить ее график.
и построить ее график.
1. Областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).
2. Точками разрыва функции являются точки х = 1, х = -1. Прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
3. Теперь найдем наклонные асимптоты.


Итак, уравнение наклонной асимптоты – y = x.
4. Найдем точки пересечения с осями Ox и Oy: Если x=0, то y=0. Если y=0, то x=0. В этом случае есть только одна точка (0,0).
5. Найдем производную функции

Критические точки: x = 0; x = -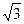 ; x =
; x = 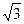 ; x = -1; x = 1. Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
; x = -1; x = 1. Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < -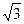 , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает
-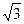 < x < -1, y¢ < 0, функция убывает
< x < -1, y¢ < 0, функция убывает
-1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x < 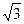 , y¢ < 0, функция убывает
, y¢ < 0, функция убывает
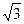 < x < ¥, y¢¢ > 0, функция возрастает
< x < ¥, y¢¢ > 0, функция возрастает
Значит, точка х = -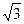 является точкой максимума, а точка х =
является точкой максимума, а точка х = 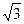 является точкой минимума. Значения функции в этих точках равны соответственно 3
является точкой минимума. Значения функции в этих точках равны соответственно 3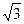 /2 и -3
/2 и -3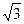 /2.
/2.
6. Найдем вторую производную функции
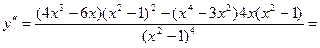

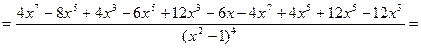
 .
.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < -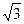 , y¢¢ < 0, кривая выпуклая
, y¢¢ < 0, кривая выпуклая
-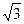 < x < -1, y¢¢ < 0, кривая выпуклая
< x < -1, y¢¢ < 0, кривая выпуклая
-1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x < 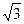 , y¢¢ > 0, кривая вогнутая
, y¢¢ > 0, кривая вогнутая
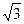 < x < ¥, y¢¢ > 0, кривая вогнутая
< x < ¥, y¢¢ > 0, кривая вогнутая
7. Построим график функции:

Домашнее задание
Исследуйте функции с помощью производной и постройте графики функций:
у = 3х2 – х3.  .
.
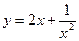 .
.
Используя правило Лопиталя, вычислите пределы функций:
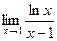 .
.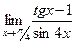 .
.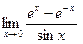 .
.
Найдите наибольшее и наименьшее значения следующих функций
(укажите точки, в которых достигаются эти значения):
у = х4 – 8х2 +3 на отрезке [–2; 2].
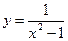 а)на отрезке
а)на отрезке 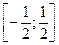 ;
;