Арифметические основы ЭВМ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра "Информатика"
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по курсу "Информатика"
по теме:
"Арифметические основы ЭВМ "
Ростов-на-Дону
Методические указания к практическим занятиям по курсу "Информатика"… Методические указания предназначены для проведения практических занятий по курсу "Информатика" у студентов…Основные понятия и определения.
Под системой счисленияпонимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
Все системы счисления делятся на позиционные и непозиционные.
Непозиционными системамиявляются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе.
Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону.
Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество  различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основаниемсистемы счисления - “
различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основаниемсистемы счисления - “ ”.
”.
В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.
Любое число N в позиционной системе счисления с основанием  может быть представлено в виде полинома от основания
может быть представлено в виде полинома от основания  :
:
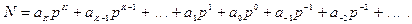 (1.1)
(1.1)
здесь  - число,
- число, 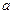 - коэффициенты (цифры числа),
- коэффициенты (цифры числа), - основание системы счисления (
- основание системы счисления ( >1).
>1).
Принято представлять числа в виде последовательности цифр:
 .
.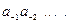
В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Точка опускается, если нет отрицательных степеней (число целое).
В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое - 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.
Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде:
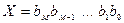 .
. ,
,
где 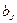 либо 0, либо 1.
либо 0, либо 1.
Эта запись соответствует сумме степеней числа 2, взятых с указанными коэффициентами:

Восьмеричная система счисления.Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таб. 1).
Таб. 1. Наиболее важные системы счисления.
|
Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр – латинскими буквами: 10–A, 11–B, 12–C, 13–D, 14–E, 15–F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таб. 1).
Перевод чисел из одной системы счисления в другую.
Перевод чисел в десятичную системуосуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
а) Перевести 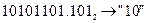 с.с. *
с.с. *
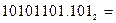

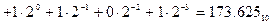
б) Перевести 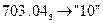 с.с.
с.с.
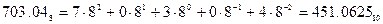
в) Перевести 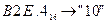 с.с.
с.с.
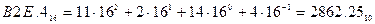 .
.
Перевод целых десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системыосуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести  с.с.
с.с.
| 176 | ||
| 16 | ||
|  6 6
|
Результат  .
.
б) Перевести  с.с.
с.с.
| 48 | ||
| 32 | ||
| 128 |  6 6
| |
  14 14
|
Результат  .
.
Перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 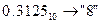 с.с.
с.с.
| 3125 ´ 8 | |
| 5000 ´ 8 | |
Результат 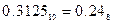 .
.
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести  с.с. Точность 6 знаков.
с.с. Точность 6 знаков.
| 65´ 2 | ||
| 3 ´ 2 | ||
| 6 ´ 2 | ||
| 2 ´ 2 | ||
| 4 ´ 2 | ||
| 8 ´ 2 | ||
| 6 ´ 2 | ||
| . . . |
Результат 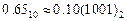 .
.
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример. Перевести 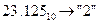 с.с.
с.с.
1) Переведем целую часть: 2) Переведем дробную часть:

| ||||

|
125 2 2
| |
25  2 2
| |
5  2 2
| |

Таким образом  ;
;  . Результат:
. Результат:  .
.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби – дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную формудостаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
Пример.
а) 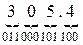 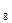 = =  ; ;
|
б)
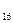 =
=  .
.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системепоступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример.
а) Перевести 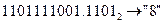 с.с.
с.с.


б) Перевести 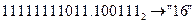 с.с.
с.с.

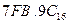
Перевод из восьмеричной в шестнадцатеричную систему и обратноосуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести  с.с.
с.с.

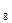
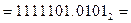
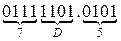
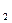
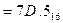
Результат: 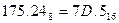 .
.
Двоичная арифметика.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения. Таблица… Пример.Выполнить сложение двоичных чисел: а) X=1101, Y=101; …Пример.
1100.011: 10.01=?
| 110001.1 | |
| – 1001 | 101.1 |
| – 1001 | |
| – 1001 | |
Результат 1100.011:10.01=101.1.
Упражнения 1.
а); б); в); г); д); е). 2. Перевести следующие числа из с.с в с.с.: а); б) ; в); г); д).Основы машинной арифметики с двоичными числами.
Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32-разрядный формат (машинное слово), 16-разрядный формат (полуслово) и 64-разрядный формат (двойное слово).
Коды чисел.
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести… 1) Разряды числа в коде жестко связаны с определенной разрядной сеткой. 2) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд. Например, если за…Пример.
Для числа +1101:
прямой код обратный код дополнительный код
0,0001101 0,0001101 0,0001101
Для числа –1101:
прямой код обратный код дополнительный код
1,0001101 1,1110010 1,1110011
Особенности сложения чисел в обратном и дополнительном кодах.
При сложении чисел в дополнительном кодевозникающая единица переноса в знаковом разряде отбрасывается. При сложении чисел в обратном кодевозникающаяединица переноса в знаковом… Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код.…Пример.
Сложить X и Y в обратном и дополнительном кодах.
а) X= 111, Y= –11;
1) Сложим числа, пользуясь правилами двоичной арифметики:
| X= 111 Y= – 11 X+Y= 100 |
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополни-тельном коде |
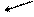 Xпр=0,0000111
Yпр=1,0000011 Xпр=0,0000111
Yпр=1,0000011
| Xобр= 0,0000111
Yобр= 1,1111100
1 0,0000011
  +1
(X+Y)обр= 0,0000100 +1
(X+Y)обр= 0,0000100
| Xдоп= 0,0000111 Yдоп= 1,1111101 1)0,0000100 отбрасывается (X+Y)доп= 0,0000100 |
Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)обр=(X+Y)доп=(X+Y)пр .
б) X= –101,Y= –11;
1) Сложим числа, пользуясь правилами двоичной арифметики:
| X= – 101 Y= – 110 X+Y= –1011 |
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополни-тельном коде |
 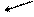 Xпр=1,0000101
Yпр=1,0000110 Xпр=1,0000101
Yпр=1,0000110
| Xобр= 1,1111010 Yобр= 1,1111001 1 1,1110011 +1 (X+Y)обр= 1,1110100 | Xдоп= 1,1111011 Yдоп= 1,1111010 1)1,1110101 отбрасывается (X+Y)доп= 1,1110101 |
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:
а) из обратного кода
(X+Y)обр=1,1110100  (X+Y)пр=1,0001011;
(X+Y)пр=1,0001011;
б) из дополнительного кода
(X+Y)доп=1,1110101 (X+Y)пр=1,0001010+0,0000001=1,0001011.
(X+Y)пр=1,0001010+0,0000001=1,0001011.
Таким образом, X+Y= –1011 и полученный результат совпадает с обычной записью
Модифицированные обратный и дополнительный коды.
При переполнении разрядной сетки, происходит перенос единицы в знаковый разряд. Это приводит к неправильному результату, причем положительное число,…Упражнения 2.
1) Записать число в прямом, обратном и дополнительном кодах: а) 11010; б) –11101; в) –101001; г) –1001110. 2) Перевести X и Y в прямой, обратный и дополнительный коды. Сложить их в обратном и дополнительном кодах. Результат…Формы представления чисел в ЭВМ.
Числа с фиксированной точкой.
Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной техники. Запись числа с фиксированной… Пример. Ячейка с целой и дробной частью.Числа с плавающей точкой.
где – основание системы счисления, – порядок числа, – мантисса числа . Положение точки определяется значением порядка . С изменением порядка точка перемещается (плавает) влево или вправо. …Пример.
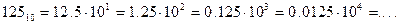
Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне:  . Таким образом, в нормализованных числах цифра после точки должна быть значащей.
. Таким образом, в нормализованных числах цифра после точки должна быть значащей.
Пример.

ненормализованное нормализованное
число число
Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка:
а) представление чисел в формате полуслова
 
|

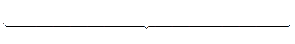
Знак Знак Порядок p Мантисса m

 (4 разряда) (10 разрядов)
(4 разряда) (10 разрядов)
б) представление чисел в формате слова
Знак Знак Порядок p Мантисса m
|
Наиболее типично представление ЧПТ в формате слова (32 разряда).
Пример.
а) Число А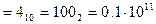 записывается в ячейку следующим образом:
записывается в ячейку следующим образом:
| . . . | |||||||||||||||||
    Знак Знак Порядок p Мантисса m
Знак Знак Порядок p Мантисса m
  (7 разрядов) (23 разряда) (7 разрядов) (23 разряда)
|
б)Число А
| . . . | ||||||||||||||||
    Знак Знак Порядок p Мантисса m
Знак Знак Порядок p Мантисса m
  (7 разрядов) (23 разряда) (7 разрядов) (23 разряда)
|
Максимальным числом представимым в формате слова будет
А

.
| . . . | ||||||||||||||||
    Зн
Зн  Зн Зн Порядок p Мантисса m Порядок p Мантисса m
|
| . . . | ||||||||||||||||
    Зн
Зн  Зн Зн Порядок p Мантисса m Порядок p Мантисса m
|
Минимальным числом из возможно представимых в формате слова будет А

Минимальным по модулю, отличным от нуля и нормализованным будет А .
.
| . . . | ||||||||||||||||
    Зн
Зн  Зн p Порядок p Мантисса m Зн p Порядок p Мантисса m
|
 
| . . . | . . . | . . . |
  Знак Знак Порядок p Мантисса m
Знак Знак Порядок p Мантисса m
  (10 разрядов) (52 разряда) (10 разрядов) (52 разряда)
|
Таким образом, числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от  до
до 
 , а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
, а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
Литература.
1. Пономарев В.С., Красников В.В. Методические указания по курсу "Организация и функционирование ЭВМ и систем". Ч. 1. Арифметические основы ЭВМ. ДГТУ, 1996.
2. Каган Б.М. Электронные вычислительные машины и системы. М.: Энергоатомиздат, 1991.
3. Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высшая школа, 1983.
4. Лю Ю-Чжен, Гибсон Г. Микропроцессоры семейства 8086/8088. М.: Радио и связь
* Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
* Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт.