рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Прямые в пространстве.
Реферат Курсовая Конспект
Прямые в пространстве.
Прямые в пространстве. - раздел Математика, Трехмерная аналитическая геометрия Векторное Уравнение Прямой. Положение Прямой В Прост...
Векторное уравнение прямой.
Положение прямой в пространстве вполне определено, если задать какую-либо точку М0 на прямой и вектор 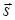 параллельный этой прямой. Вектор
параллельный этой прямой. Вектор 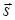 называется направляющим вектором прямой. Пусть прямая линия l задана её точкой М0(х0; у0; z0) и направляющим вектором
называется направляющим вектором прямой. Пусть прямая линия l задана её точкой М0(х0; у0; z0) и направляющим вектором 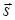 (m; n; p). Тогда
(m; n; p). Тогда
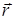 =
=  + t
+ t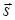 , tÎR. (2)
, tÎR. (2)
Это уравнение называется векторным уравнением прямой.
Параметрические уравнения прямой.
Учитывая, что 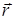 = (x; y; z); r0 = (х0; у0; z0); t
= (x; y; z); r0 = (х0; у0; z0); t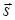 = (tm; tn; tp) уравнение (2) можно записать в виде:
= (tm; tn; tp) уравнение (2) можно записать в виде:
x + y
+ y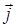 + z
+ z = (x0 + tm)
= (x0 + tm) + (y0 + tn)
+ (y0 + tn)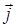 + (z0 + tp)
+ (z0 + tp) .
.
Получаем систему равенств:
х = x0 + tm
y = y0 + tn
z = z0 + tp, tÎR.
Эта система задает параметрические уравнения прямой в пространстве.
Канонические уравнения прямой.
Пусть 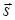 (m; n; p) – направляющий вектор прямой l и точка М0(х0; у0; z0) – точка, лежащая на этой прямой. Двойное равенство
(m; n; p) – направляющий вектор прямой l и точка М0(х0; у0; z0) – точка, лежащая на этой прямой. Двойное равенство
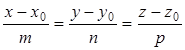 (3)
(3)
называется каноническим уравнением прямой в пространстве. Отметим, что
обращение в 0 одного из знаменателей канонического уравнения означает обращение в 0 соответствующего числителя. Например, каноническое уравнение
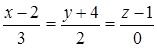
задает прямую, проходящую через точку М0(2; –4; 1) перпендикулярно оси Oz (проекция вектора 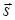 на Oz равна 0, но это означает, что прямая лежит в плоскости z=1 и поэтому для всех точек прямой будет z–1=0)
на Oz равна 0, но это означает, что прямая лежит в плоскости z=1 и поэтому для всех точек прямой будет z–1=0)
Уравнение прямой, проходящей через две точки в пространстве
Две различные точки М1(х1; у1; z1), М2(х1; у1; z1) задают единственную прямую l. Уравнение прямой, проходящей через 2 точки, имеет вид
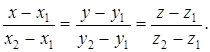
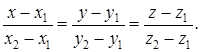
(4)
Общие уравнения прямой в пространстве
Прямую в пространстве можно задать, как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений:
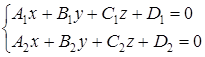 (5)
(5)
Каждое из уравнений этой системы определяет плоскость: первое уравнение – плоскость a1, второе – плоскость a2. Если плоскости a1 и a2 непараллельные (т.е. координаты векторов 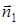 (A1;B1;C1) и
(A1;B1;C1) и  (A2;B2;C2) непропорциональны), то система (5) определяет прямую l, как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. Уравнения (5) называют общими уравнениями прямой.
(A2;B2;C2) непропорциональны), то система (5) определяет прямую l, как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. Уравнения (5) называют общими уравнениями прямой.
От общих уравнений прямой (5) можно перейти к каноническим уравнениям (3). Координаты точки М0 на прямой l получаем из системы (5), придав одной из координат произвольное значение (например: z=0). Так как прямая l перпендикулярна векторам 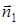 и
и  , то за направление
, то за направление  прямой l можно принять векторное произведение
прямой l можно принять векторное произведение 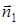 ´
´ :
:


Замечание. каноническое уравнение прямой легко получить, взяв две какие-либо точки на ней и применив уравнение (4).
Пример. написать каноническое уравнение прямой
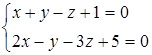
Решение.
Положим что z = 0
Положим что у=0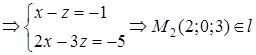
Записываем уравнение прямой l, проходящей через точки М1 и М2
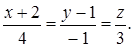
Угол между прямыми в пространстве.
Условия параллельности и перпендикулярности прямых
Пусть прямые l1 и l2 заданы уравнениями:
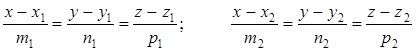
Под углом между этими прямыми понимают угол между направляющими векторами 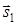 (m1; n1; p1) и
(m1; n1; p1) и 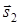 (m2; n2; p2). Поэтому по формуле для косинуса угла между векторами имеем
(m2; n2; p2). Поэтому по формуле для косинуса угла между векторами имеем
 (6)
(6)
Для нахождения острого угла между прямыми l1 и l2, числитель правой части в (6) следует взять по модулю. Если прямые l1 и l2 перпендикулярны, то cos φ = 0, что означает
m1m2 + n1n2 + p1p2 = 0.
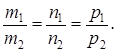
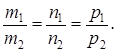
Если прямые l1 и l2 параллельны, то
Условие, при котором две прямые лежат в одной плоскости
Пусть прямые l1 и l2 заданы каноническими уравнениями
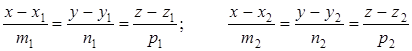
Соответственно их направляющие векторы 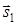 (m1; n1; p1) и
(m1; n1; p1) и 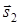 (m2; n2; p2). Прямая l1 проходит через точку М1(х1; у1; z1), радиус-вектор которой обозначим
(m2; n2; p2). Прямая l1 проходит через точку М1(х1; у1; z1), радиус-вектор которой обозначим 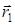 . Прямая l2 проходит через точку М2(х2; у2; z1), ее радиус-вектор обозначим
. Прямая l2 проходит через точку М2(х2; у2; z1), ее радиус-вектор обозначим  .
.
Тогда
 –
– 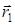 =
=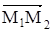 = (х2 – х1; y2 – y1; z2 – z1).
= (х2 – х1; y2 – y1; z2 – z1).
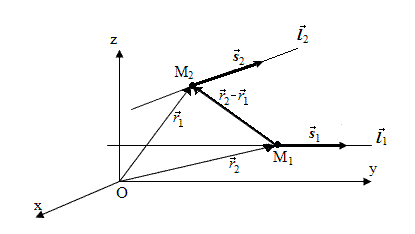
Прямые l1 и l2 лежат в одной плоскости, если векторы  ,
,  и
и 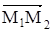 компланарны. Условием компланарности трех векторов является равное нулю их смешанное произведение, то есть: ([
компланарны. Условием компланарности трех векторов является равное нулю их смешанное произведение, то есть: ([ –
– 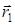 ]´
]´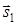 ,
, 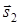 ) = 0 или
) = 0 или

– Конец работы –
Эта тема принадлежит разделу:
Трехмерная аналитическая геометрия
На сайте allrefs.net читайте: Трехмерная аналитическая геометрия.
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Прямые в пространстве.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов