Решить систему уравнений по правилу Крамера
Матрицы можно перемножить только тогда, когда кол-во столбцов 1-ой матрицы равно кол-ву строк 2-ой и наоборот.
Так как знаки миноров элементов второй строки противоположны знакам миноров элементов первой строки, то
 .
.
Вырожденная – определитель равен нулю, невырожденная – не равен нулю.
В заключение перечислим свойства операций над матрицами:
1) А+В = В+А;
2) А+(В+С) = (А+В)+С;
3) (α+β)А=αА+βА,где α и β – числа;
α(А+В) = αА+ αВ; (αβ)А = α(βА);
4) А(ВС) = (АВ)С; А(В+С) = АВ+АС;
5) А+0 = А;
6) АЕ = ЕА = А.
Пример 12.
Пусть  .
.
Найти значение многочлена 
Решение. Подставим вместо x под знак многочлена матрицу A.
Тогда , где
, где  , а вместо числа 4 мы ввели матрицу
, а вместо числа 4 мы ввели матрицу  , так как складывать можно только матрицы одинакового размера, но не матрицу с числом.
, так как складывать можно только матрицы одинакового размера, но не матрицу с числом.
Вычислим  . Имеем
. Имеем
 .
.
Далее 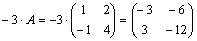 ,
,
 .
.

Решить систему уравнений по правилу Крамера:

Решение. вычислим определитель системы:
 то есть система совместна.
то есть система совместна.
Найдем далее вспомогательные определители:



Тогда х1=30, х2=20, х3=-60.
Пример 17. Матричным методом решить систему уравнений

Решение. Вычислим определитель матрицы А.

то есть матрица А невырожденная. Построим обратную матрицу А-1. Вычислим алгебраические дополнения элементов матрицы А:

Следовательно,
 .
.
Находим теперь решение системы по формуле (1.12).


то есть x = 3, y = 1, z = -1.
Пример 19. Исследовать совместность системы
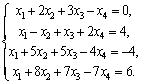
Решение. Произведем элементарные преобразования расширенной матрицы системы

Первую строку матрицы умножим на –1 и прибавим ее к остальным строкам. Получим
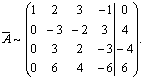
Вторую строку полученной матрицы сложим с третьей строкой, а затем, умножив ее на 2, сложим с последней:

Ранг матрицы системы равен двум, а ранг расширенной – трем. Следовательно, система несовместна.
Пример 20. Исследовать совместность и найти общее решение системы

Решение. Произведем элементарные преобразования расширенной матрицы системы
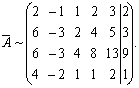
Умножив первую строку матрицы на –3, сложим ее со второй и третьей строками, а, умножив на –2, сложим ее с четвертой строкой.
Тогда имеем

Сложим теперь вторую строку этой матрицы с третьей и вычтем ее из четвертой:

Так как расширенная матрица системы  и матрица системы А содержат три ненулевых строки, то
и матрица системы А содержат три ненулевых строки, то  Система совместна и, так как ранг матрицы
Система совместна и, так как ранг матрицы  меньше числа неизвестных системы, то система имеет множество решений.
меньше числа неизвестных системы, то система имеет множество решений.
Выберем в качестве базисного минора
 Тогда неизвестные х2, х3, х4 – базисные, а х1 и х5 – свободные. Укороченная система имеет вид
Тогда неизвестные х2, х3, х4 – базисные, а х1 и х5 – свободные. Укороченная система имеет вид

Положим х1=с1, х5=с2. Тогда система примет вид

Так как х4=0, то из второго уравнения этой системы х3=3-4с2.
Подставляя х4 и х3 в первое уравнение, получим

Следовательно, общее решение исходной системы имеет вид

Пример 21. Решить систему

Решение. Составим матрицу системы

и методом элементарных преобразований найдем ранг
 r=2.
r=2.
Выберем в качестве базисного минор  Тогда укороченная система имеет вид
Тогда укороченная система имеет вид

Полагая х3=с1, х4=с2, находим х2=-6с1+5с2, а х1=-4с1+3с2+2(6с1-5с2)=8с1-7с2. Общее решение системы
 (1.20)
(1.20)
Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что свободным неизвестным дают последовательно значения

Матрицы-столбцы, то есть фундаментальную систему решений обозначают Е1, Е2, …, Еn. Общее решение будет представлено в виде
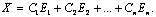
В примере 21 найти фундаментальную систему решений и выразить с ее помощью общее решение этой системы.
Из общего решения (1.20) системы найдем фундаментальную систему решений.
 ,
, 
С использованием фундаментальной системы общее решение можно записать в виде

Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых (обозначают  , а также
, а также  , если векторы сонаправлены, и
, если векторы сонаправлены, и  , если они противоположно направлены).
, если они противоположно направлены).
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Два вектора называются равными, если они сонаправлены ( ) и имеют равные длины (
) и имеют равные длины ( ). Обозначают
). Обозначают  .
.
Для каждого вектора  , отличного от нулевого вектора, существует противоположный вектор, который обозначается
, отличного от нулевого вектора, существует противоположный вектор, который обозначается  и удовлетворяет условиям:
и удовлетворяет условиям:  ,
, 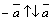 .
.
a(x1,y1,z1)+(-)b(x2 ,y2,z2)=c(x1+(-)x2,y1+(-)y2,z1+(-)z2)
A*a(x1,y1,z1)= a(A*x1,A*y1,A*z1)
Проекцией вектора  на ось
на ось  (обозначается пр
(обозначается пр ) называется длина его составляющей
) называется длина его составляющей  по этой оси, взятая со знаком «плюс», если
по этой оси, взятая со знаком «плюс», если  , и со знаком «минус», если
, и со знаком «минус», если  .
.
Очевидно, что пр , если вектор
, если вектор  образует острый угол с осью
образует острый угол с осью  ; пр
; пр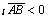 , если этот угол тупой; пр
, если этот угол тупой; пр , если
, если  .
.
Если известны координаты точек  и
и  на оси:
на оси:  ,
,  , то пр
, то пр .
.
Нетрудно доказать свойства проекций:
1) Равные векторы имеют равные проекции на одну и ту же ось.
2) пр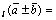 пр
пр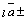 пр
пр .
.
3) пр aпр
aпр ,
,  .
.
4) пр , где
, где  – угол между вектором и осью.
– угол между вектором и осью.
Заметим, что проекция вектора на ось и его составляющая связаны соотношением сост пр
пр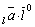 .
.

Это равенство называется разложением вектора 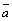 по базису
по базису  ,
,  ,
,  , а числа
, а числа  ,
,  ,
, 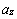 называются координатами вектора
называются координатами вектора 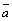 в этом базисе, или декартовыми прямоугольными координатами вектора. Пишут
в этом базисе, или декартовыми прямоугольными координатами вектора. Пишут  или
или  .
.
Таким образом, прямоугольные декартовы координаты вектора – это его проекции на соответствующие оси координат.
Зная координаты вектора, легко выразить его длину:


Из свойств проекций (а координаты вектора – это его проекции на оси координат) следует:
если  ,
,  ,
,  , то
, то
1)  ,
, 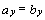 ,
, 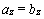 – равные векторы имеют соответственно равные координаты;
– равные векторы имеют соответственно равные координаты;
2)  – при сложении векторов их координаты складываются, при вычитании – вычитаются;
– при сложении векторов их координаты складываются, при вычитании – вычитаются;
3)  – при умножении вектора на число его координаты умножаются на это число;
– при умножении вектора на число его координаты умножаются на это число;
4)  ,
,  ,
,  , то есть
, то есть  – (2.4)
– (2.4)
координаты коллинеарных векторов пропорциональны.
Из свойств проекций: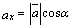 ,
,  ,
,  . Следовательно,
. Следовательно,
 ,
,  ,
,  .
.
Говорят, что точка  делит отрезок
делит отрезок 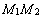 в отношении
в отношении  , если
, если  , или
, или  (рис. 13).
(рис. 13).

Рис. 13
Пусть координаты точек  и
и 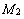 известны:
известны: 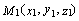 ,
, 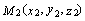 . Найдем координаты точки
. Найдем координаты точки  . Очевидно, что
. Очевидно, что 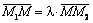 , где
, где  ,
,  . Приравнивая координаты векторов, найдем:
. Приравнивая координаты векторов, найдем:
 ,
,  ,
,  . (2.6)
. (2.6)
В частности, если  – середина отрезка
– середина отрезка 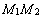 , то
, то  , тогда
, тогда
 ,
,  ,
,  .
.
Пример 5.
Показать, что точки , , лежат на одной прямой, причем A – между B и C.
, ; , следовательно, . Координаты вектора больше, значит, он длиннее и точка A лежит между B и…Даны вершины треугольника , , . Найти точку пересечения медиан этого треугольника и орт вектора (рис. 14).
Решение. AD – медиана, следовательно, D – середина
отрезка BC, ее координаты находятся по формулам (2.7):
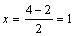 ,
,  ,
,  , то есть
, то есть  . Медианы точкой пересечения K делятся в отношении 2:1, значит,
. Медианы точкой пересечения K делятся в отношении 2:1, значит,  , тогда по формулам (2.6) найдем координаты точки K:
, тогда по формулам (2.6) найдем координаты точки K:  ,
, 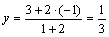 ,
, 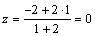 . Таким образом, точка пересечения медиан –
. Таким образом, точка пересечения медиан –  . Найдем координаты вектора
. Найдем координаты вектора 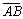 по формуле (2.3) и его длину по формуле (2.2):
по формуле (2.3) и его длину по формуле (2.2):  ;
;  . Координаты единичного вектора совпадают с его направляющими косинусами. По формулам (2.5)
. Координаты единичного вектора совпадают с его направляющими косинусами. По формулам (2.5)  ,
,  ,
,  , следовательно,
, следовательно,  – орт вектора
– орт вектора 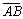 .
.
Скалярным произведением двух векторов (обозначается  или
или  ) называется число, равное произведению длин этих векторов на косинус угла между ними:
) называется число, равное произведению длин этих векторов на косинус угла между ними: 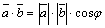 , где
, где 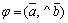 .
.
Свойства скалярного произведения:
1)  ;
;
2)  ;
;
3) 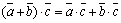 ;
;
4)  , или
, или  , или
, или 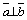 .
.
Таким образом, 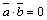 – условие перпендикулярности векторов.
– условие перпендикулярности векторов.
5)  , или, обозначая
, или, обозначая  (скалярный квадрат вектора
(скалярный квадрат вектора  ), получим
), получим  , откуда
, откуда 
Пример 6. Найти угол между диагоналями параллелограмма, построенного на векторах и .
Решение. Диагоналями параллелограмма являются векторы  и
и  (см. рис. 5). Тогда
(см. рис. 5). Тогда 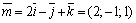 ,
,  ,
, 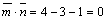 , следовательно,
, следовательно,  – угол между диагоналями равен
– угол между диагоналями равен 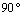 .
.
Пример 7.Дано:  ,
, 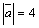 ,
,  ,
,  . Вычислить
. Вычислить 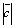 – длину вектора
– длину вектора  .
.
Решение. Из свойства (5) скалярного произведения  ; но
; но  ,
, 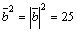 ,
,  , следовательно,
, следовательно,  .
.
Векторным произведением двух векторов называется вектор, который обозначается  или
или  и определяется следующим образом:
и определяется следующим образом: 
1)  где
где  – длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними;
– длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними;
2) `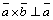 ,`
,` – этот вектор перпендикулярен каждому из перемножаемых векторов;
– этот вектор перпендикулярен каждому из перемножаемых векторов;
3) векторы 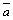 ,
, 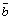 ,
,  образуют правую тройку.
образуют правую тройку.
Из условия (1) следует, что модуль вектора` численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах  и
и 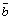 как на сторонах (рис 17):
как на сторонах (рис 17):  ,
,  .
.
Свойства векторного произведения:
1)  ;
;
2) 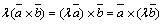 ;
;
3)  ;
;
4)  , или
, или  , или
, или  ;
;
4a) 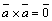 .
.
Пример 8. Упростить выражение  .
.
Решение. На основании свойств векторного произведения получим 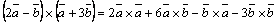 , но
, но  ,
,  , тогда
, тогда 
 .
.
Пример 9. В треугольнике с вершинами  ,
,  ,
,  найти длину высоты
найти длину высоты 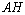 .
.
Решение.  , откуда
, откуда  , где
, где 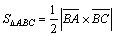 . Найдем координаты векторов:
. Найдем координаты векторов:  ,
,  .
.
Тогда

 , то есть
, то есть  ;
;
 , следовательно,
, следовательно,  .
.
По определению скалярного произведения 
 , где
, где  – угол между векторами
– угол между векторами 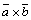 и
и 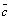 . Но
. Но  – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах  и
и  , а
, а 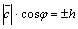 , где
, где  – высота параллелепипеда. Таким образом,
– высота параллелепипеда. Таким образом,  .
.
Смешанное произведение трех векторов с точностью до знака равно объему параллелепипеда, построенного на этих векторах как на ребрах. Можно записать:  .
.
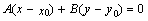 - уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
- уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
 – общее уравнение прямой на плоскости.
– общее уравнение прямой на плоскости.
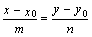 - каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.
- каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.
y0, x0 – заданные координаты данного вектора
 , – параметрические уравнения прямой.
, – параметрические уравнения прямой.
 – уравнение прямой, проходящей через две данные точки.
– уравнение прямой, проходящей через две данные точки.
Угол между двумя прямыми.Пусть прямые  и
и  заданы соответственно уравнениями
заданы соответственно уравнениями  ,
,  , где
, где 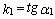 ,
,  . Обозначим
. Обозначим  угол между прямыми:
угол между прямыми:  (рис. 24). Тогда
(рис. 24). Тогда  ,
,  .
.

Рис. 24
Таким образом,
 . (2.20)
. (2.20)
Если  , то
, то 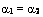 , а следовательно,
, а следовательно,  , то есть k1= k2.
, то есть k1= k2.
Если 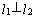 , то
, то  ,
,  не определен,
не определен,  , следовательно,
, следовательно,  , или
, или  .
.
Если прямые  и
и  заданы соответственно уравнениями
заданы соответственно уравнениями
 ,
,  , где
, где  ,
,  – нормальные векторы прямых, то
– нормальные векторы прямых, то , или
, или  .
.
Если  , то
, то  , следовательно,
, следовательно,  .
.
Если 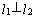 ,
,  , то есть
, то есть  .
.
Расстояние от точки до прямой.Пусть прямая  на плоскости задана уравнением
на плоскости задана уравнением 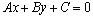 и точка
и точка 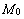 имеет координаты
имеет координаты  (рис. 25). Обозначим
(рис. 25). Обозначим 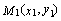 – основание перпендикуляра, опущенного из точки
– основание перпендикуляра, опущенного из точки 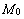 на прямую
на прямую  ,
,  ,
,  – расстояние от точки
– расстояние от точки 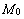 до прямой
до прямой  . Тогда
. Тогда  , а
, а  – нормальный вектор прямой. Рассмотрим скалярное произведение
– нормальный вектор прямой. Рассмотрим скалярное произведение  . С одной стороны,
. С одной стороны,  , так как
, так как  , следовательно, угол между ними
, следовательно, угол между ними  или
или . С другой стороны,
. С другой стороны,  , но точка
, но точка  , поэтому ее координаты удовлетворяют уравнению
, поэтому ее координаты удовлетворяют уравнению  , откуда
, откуда  , поэтому
, поэтому  . Приравнивая выражения, получим
. Приравнивая выражения, получим
 . Тогда
. Тогда  или
или
 . (2.21)
. (2.21)

Пример 12. Прямая  задана уравнением
задана уравнением  . Составить уравнения а) прямой
. Составить уравнения а) прямой 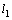 , проходящей через точку
, проходящей через точку  параллельно прямой
параллельно прямой  ; б) прямой
; б) прямой  , проходящей через начало координат перпендикулярно прямой
, проходящей через начало координат перпендикулярно прямой  .
.
Решение. 1-й способ. Из уравнения прямой  определим нормальный вектор этой прямой
определим нормальный вектор этой прямой  . Этот вектор перпендикулярен и прямой
. Этот вектор перпендикулярен и прямой 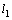 (рис. 26). Таким образом, для
(рис. 26). Таким образом, для 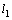 известен нормальный вектор
известен нормальный вектор  и точка
и точка 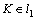 . Воспользуемся уравнением (2.12):
. Воспользуемся уравнением (2.12):  или
или 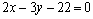 – уравнение
– уравнение 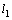 . Для прямой
. Для прямой  вектор
вектор  является направляющим
является направляющим  и точка
и точка  . Воспользуемся уравнением (2.15):
. Воспользуемся уравнением (2.15): 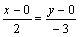 , или
, или  , или
, или 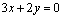 – уравнение
– уравнение  .
.

Рис. 26
2-й способ. Запишем уравнение прямой  в виде
в виде  . Найдем угловой коэффициент прямой
. Найдем угловой коэффициент прямой  :
:  . Прямая
. Прямая  , следовательно, ее угловой коэффициент
, следовательно, ее угловой коэффициент  ; прямая
; прямая  , поэтому ее угловой коэффициент
, поэтому ее угловой коэффициент 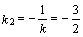 . Зная угловой коэффициент прямой и координаты точки на этой прямой, можно воспользоваться уравнением (2.18). Получим уравнение прямой
. Зная угловой коэффициент прямой и координаты точки на этой прямой, можно воспользоваться уравнением (2.18). Получим уравнение прямой 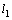 :
: 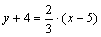 или, умножив обе части на 3,
или, умножив обе части на 3, 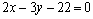 , и уравнение прямой
, и уравнение прямой  :
:  , то есть
, то есть  .
.
Пример 13. В треугольнике с вершинами  ,
,  ,
,  составить уравнения медианы
составить уравнения медианы  , высоты
, высоты 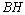 , найти длину высоты
, найти длину высоты 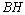 (рис. 27).
(рис. 27).

Рис. 27
Решение.  – середина отрезка
– середина отрезка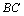 , ее координаты найдем по формулам (2.7):
, ее координаты найдем по формулам (2.7):  ,
,  , то есть
, то есть  . Таким образом, на медиане известны две точки
. Таким образом, на медиане известны две точки  и
и  . Воспользуемся уравнением (2.17):
. Воспользуемся уравнением (2.17):  , или
, или  – уравнение медианы
– уравнение медианы  . Его можно привести к виду
. Его можно привести к виду  . Для составления уравнения высоты
. Для составления уравнения высоты 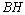 найдем
найдем  – нормальный вектор прямой ВН. Воспользуемся уравнением (2.12):
– нормальный вектор прямой ВН. Воспользуемся уравнением (2.12):  . Разделив на 4 и раскрыв скобки, получим
. Разделив на 4 и раскрыв скобки, получим  – уравнение
– уравнение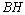 . Составим уравнение прямой
. Составим уравнение прямой  , используя уравнение (2.15) и рассматривая
, используя уравнение (2.15) и рассматривая  как направляющий вектор:
как направляющий вектор: 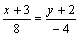 ;
;  , или
, или  . Тогда длину высоты
. Тогда длину высоты 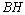 найдем по формуле (2.21) как расстояние от точки
найдем по формуле (2.21) как расстояние от точки  до прямой
до прямой  :
: 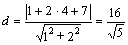 .
.
 – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
– уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
 – общее уравнение плоскости.
– общее уравнение плоскости.
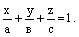 – уравнение плоскости в отрезках. Здесь а, в, с – отрезки, отсекаемые плоскостью на осях координат
– уравнение плоскости в отрезках. Здесь а, в, с – отрезки, отсекаемые плоскостью на осях координат
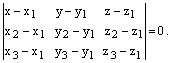 – уравнение плоскости, проходящей через три данные точки.
– уравнение плоскости, проходящей через три данные точки.
Неполные уравнения плоскостей
Если в уравнении плоскости 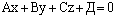 какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости
какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости
Пусть, например,  Уравнение имеет вид
Уравнение имеет вид  и определяет плоскость, проходящую через начало координат (координаты точки О(0; 0; 0) удовлетворяют уравнению).
и определяет плоскость, проходящую через начало координат (координаты точки О(0; 0; 0) удовлетворяют уравнению).
Пусть  Уравнение имеет вид
Уравнение имеет вид  и определяет плоскость, параллельную оси Оz или проходящую через ось Оz при
и определяет плоскость, параллельную оси Оz или проходящую через ось Оz при  Действительно, тогда
Действительно, тогда  то есть
то есть  а плоскость
а плоскость 
Пусть  Уравнение имеет вид
Уравнение имеет вид 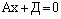 и определяет плоскость, параллельную плоскости Оуz или совпадающую с ней при
и определяет плоскость, параллельную плоскости Оуz или совпадающую с ней при  Действительно,
Действительно,  то есть
то есть 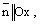 а плоскость
а плоскость  или
или 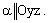
Аналогично можно рассмотреть другие случаи.
Угол между двумя плоскостями
Пусть плоскости a1 и a2 заданы соответственно уравнениями 
 где
где 
 и
и  – нормальные векторы этих плоскостей (рис. 45). Очевидно,
– нормальные векторы этих плоскостей (рис. 45). Очевидно, 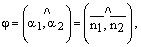 тогда косинус угла между плоскостями
тогда косинус угла между плоскостями 
| Расстояние от точки до плоскости | |||||||||
Если  – заданная точка и – заданная точка и  – уравнение плоскости a, то расстояние от точки Мо до плоскости a определяется по формуле: – уравнение плоскости a, то расстояние от точки Мо до плоскости a определяется по формуле:
(доказывается аналогично (2.21)). | |||||||||
| § 14. Прямая в пространстве | |||||||||
Прямую в пространстве можно задать уравнениями, аналогичными уравнениям прямой на плоскости:
– канонические уравнения, здесь хо, уо, zо – координаты заданной точки на прямой, а m, n, p – координаты направляющего вектора прямой (вектора, параллельного прямой);
– параметрические уравнения прямой;
– уравнения прямой, проходящей через две данные точки М1(х1, у1, z1) и М2(х2, у2, z2). Прямую в пространстве можно задать также как линию пересечения двух плоскостей. Если уравнения этих плоскостей
(2.37) – общие уравнения прямой в пространстве. Для нахождения какой-нибудь точки на этой прямой достаточно придать одной из переменных конкретное числовое значение (например, х = 0), подставить его в систему (2.37) и решить ее относительно двух оставшихся переменных. Направляющий вектор прямой (2.37) можно найти как векторное произведение нормальных векторов пересекающихся плоскостей: Пример 21. Записать канонические уравнения прямой, заданной общими уравнениями Решение. Найдем точку на прямой. Пусть, например, z = 0. Система примет вид | |||||||||
| Угол между прямыми | ||||
Пусть прямые  и и  заданы каноническими уравнениями заданы каноническими уравнениями  и и  Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых:  Тогда Тогда
Если Если | ||||
| § 15. Взаимное расположение прямой и плоскости | ||||
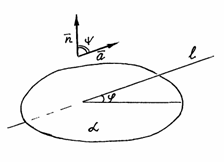
Пусть плоскость a задана уравнением  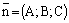 – ее нормальный вектор, а прямая – ее нормальный вектор, а прямая  задана уравнениями задана уравнениями 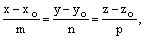  – направляющий вектор прямой. Обозначим – направляющий вектор прямой. Обозначим  – угол между прямой и плоскостью, – угол между прямой и плоскостью,  – угол между соответствующими векторами (рис.46). Очевидно, – угол между соответствующими векторами (рис.46). Очевидно,  а а  или или  Но Но  тогда синус угла между прямой и плоскостью можно найти по формуле тогда синус угла между прямой и плоскостью можно найти по формуле
Рис. 46 Если
– условие параллельности прямой и плоскости. При этом же условии прямая лежит в плоскости.
Рис. 47 Если Пусть требуется найти точку пересечения прямой
Рис. 48 Замечание. Если уравнение относительно t примет вид 0t = 0 (то есть M = N = 0), то любое действительное значение t будет его решением, значит, прямая и плоскость имеют множество общих точек, то есть прямая лежит в плоскости. Если уравнение относительно t примет вид 0 × t = N (то есть М = 0, N ¹ 0), то такое уравнение решений не имеет, значит, прямая и плоскость не имеют общих точек, то есть прямая параллельна плоскости. Пример 22. Найти точку пересечения прямой Решение. Запишем параметрические уравнения прямой: Пример 23. Показать, что прямая Решение. 1-й способ. Используем параметрические уравнения прямой 2-й способ. |



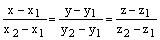
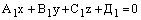 и
и  где
где 
 – их нормальные векторы, то уравнения прямой (их линии пересечения) имеют вид
– их нормальные векторы, то уравнения прямой (их линии пересечения) имеют вид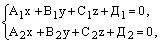


 Сложив уравнения, получим
Сложив уравнения, получим 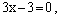
 Тогда из второго уравнения
Тогда из второго уравнения  Точка на прямой А(1; -2; 0). Найдем направляющий вектор этой прямой:
Точка на прямой А(1; -2; 0). Найдем направляющий вектор этой прямой: 
 Получим канонические уравнения прямой
Получим канонические уравнения прямой 

 то
то 
 , то
, то  или
или 
 .
.
 то
то  (рис. 47), то есть
(рис. 47), то есть  или
или

 то
то  (рис. 48), то есть
(рис. 48), то есть  – условие перпендикулярности прямой и плоскости.
– условие перпендикулярности прямой и плоскости.

 и подставим выражения для х, у, z в уравнение плоскости. Получим уравнение вида
и подставим выражения для х, у, z в уравнение плоскости. Получим уравнение вида  относительно параметра t. Выразив t и подставив в параметрические уравнения, найдем координаты точки пересечения.
относительно параметра t. Выразив t и подставив в параметрические уравнения, найдем координаты точки пересечения.
 и плоскости
и плоскости 
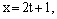
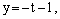
 Подставим эти выражения в уравнение плоскости:
Подставим эти выражения в уравнение плоскости: 

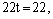
 Из параметрических уравнений получим
Из параметрических уравнений получим 

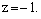 Следовательно, точка пересечения прямой и плоскости
Следовательно, точка пересечения прямой и плоскости 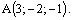
 лежит в плоскости
лежит в плоскости 


 Подставим в уравнение плоскости:
Подставим в уравнение плоскости: 
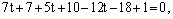
 – получили равенство, верное при любых
– получили равенство, верное при любых  Следовательно, прямая лежит в плоскости.
Следовательно, прямая лежит в плоскости. – направляющий вектор прямой,
– направляющий вектор прямой,  – нормальный вектор плоскости.
– нормальный вектор плоскости.  значит, прямая параллельна плоскости или лежит в плоскости (из условия (2.40)). Точка
значит, прямая параллельна плоскости или лежит в плоскости (из условия (2.40)). Точка  принадлежит прямой и ее координаты удовлетворяют уравнению плоскости:
принадлежит прямой и ее координаты удовлетворяют уравнению плоскости: 
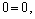 значит, прямая лежит в плоскости.
значит, прямая лежит в плоскости.