УРАВНЕНИЕ ШРЕДИНГЕРА

Л Е К Ц И Я 3

 

ВОЛНОВАЯ ФУНКЦИЯ ЧАСТИЦЫ

УРАВНЕНИЕ ШРЕДИНГЕРА

|cxñ = x|cxñ.   Разложим по всем таким состояниям произвольный вектор |yñ:

Если в классической механике некоторая динамическая величина есть функция каких-то других динамических величин, то при переходе к квантовой механике функциональная зависимость между величинами сохраняется.

Пример применения этого правила для написания оператора Гамильтона будет рассмотрен чуть ниже, а сейчас подведем некоторые итоги.

 

 

РЕЗЮМЕ

 

В квантовой механике волновая функция зависит от (обобщенных) координат q и времени t: y = y (q, t), и ее эволюция определяется уравнением Шредингера

i= ,

где - оператор Гамильтона. Это - реализация принципа причинности. Если внешние поля не зависят явно от времени, то частные решения имеют вид

y (q, t) = Q(t)×y (q),

 

причем функции y и Q подчиняются уравнениям

y_E (q) = E y_E (q), ii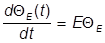(t).

 

Первое из них есть уравнение на собственные значения оператора Гамильтона и называется стационарным уравнением Шредингера. Оно определяет энергетический спектр {Е} системы и собственные функции y_E(q), т.е. функции состояний, в которых энергия имеет определенные значения E. Если найдены значения E, то можем решать второе уравнение:

Q_E (t) = .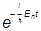

 

В результате получим набор состояний с волновыми функциями

y_E(q, t) = 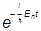y_E (q) ,

в которых энергия имеет определенные значения. Такие состояния называются стационарными. Они обобщают понятие боровских стационарных орбит. В стационарном состоянии плотность вероятности

 

r (q, t) = | y_E (q, t) |² = | y_E (q) |² ,

 

т.е. она не зависит от времени. Не зависят от времени и средние значения физических величин.

 

Рассмотрим теперь пример. Пусть частица движется во внешнем поле. В классической механике ее функция гамильтона есть

H = .

 

В квантовой механике получим оператор Гамильтона

 

= =+V(r,t).

 

Уравнение Шредингера будет записываться как

 

= {+}y(r,t).

 

Стационарное уравнение Шредингера имеет вид:

y_E (r) = Е y_E (r) Þ {+V(r) } y_E (r) = Е y_E (r)

 

(здесь уже считается, что V не зависит от времени, иначе разделение переменных не возможно).

Запишем уравнение, сопряженное уравнению Шредингера (УШ):

 

-= {+V(r)}y^* (r,t).

 

Умножая УШ слева на y^*, а сопряженное УШ - слева на y и производя вычитание, получим:

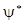
º = (-) º

º (.

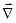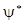
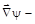
Величина

r (r,t) = |y(r,t) |²

 

есть плотность вероятности. Введем вектор

j(r,t) = 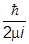(y^*y,

чтобы записать в компактной форме полученное соотношение:

 

+ div j= 0.

 

Это есть уравнение непрерывности. Оно выражает закон сохранения вероятности. Поскольку r - плотность вероятности, то j следует интерпретировать как плотность потока вероятности.

В стационарном случае, когда V = V(r) волновые функции стационарных состояний имеют вид

y(r,t) = 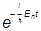y_E (r),

 

где y_E подчиняется уже выписанному стационарному уравнению Шредингера. Для плотности вероятности и плотности потока вероятности получаем не зависящие от времени величины:

 

r = | y_E (r)|², j= 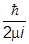.