МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ

Возьмем какой-то эрмитов оператор 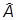и поставим задачу на собственные значения:

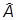|j_nñ = A_n|j_nñ.

Допустим, что спектр - чисто дискретный. Это значит, что собственные векторы образуют ортонормированный базис:

 

(j_n, j_m) = d_nm Û áj_n|j_mñ = d_nm,

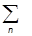|j_nñáj_n| = .

 

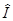Любой вектор |yñ можно разложить по этому базису:

|yñ = 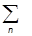y_n|j_nñ,

 

где дискретная последовательность коэффициентов Фурье

 

y_n = áj_n|yñ

будет однозначно задавать состояние y. Расположим числа y_n в матрицу - столбец:

|yñ = .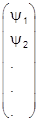

Она и представляет вектор состояния |yñ. Образуем эрмитово сопряженную матрицу, которая будет матрицей - строкой с компонентами

 

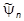= áj_n |yñ^* = áy|j_nñ = y^*_n.

Она будет представлять совектор áy| :

áy|= (y^*₁, y^*₂,...).

 

С использованием условия полноты 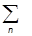|j_nñáj_n| = 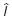скалярный квадрат запишется как

 

áy |y ñ = 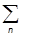áy | j_nñá j_n|yñ = 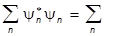|y_n|² .

Если вектор |y ñ нормирован, т.е. áy |y ñ=1, то сумма также равна 1, т.е. ряд сходится.

Рассмотрим теперь некоторый оператор 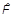,который действуя на |y ñ переводит его в :

 

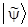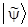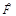= |y ñ.

 

Умножая скалярно на á j_n| и пользуясь условием полноты, найдем:

 

á j_n| y ñ = á j_n|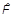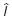|y ñ = 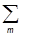á j_n|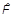| j_mñá j_m |y ñ,

или

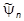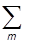=F_nmy_m,

 

где введена матрица оператора:

 

F_nm º á j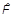_n| |j_mñ.

 

Оператор 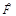переводит |yñ в 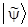, а матрица F_nm переводит компоненты y_n вектора |yñ в компоненты 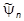вектора 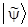. Если оператор эрмитов, то и его матрица эрмитова:

 

F_nm = (F_mn)^*.

 

Среднее значение оператора 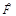в состоянии y теперь вычисляется так:

áFñ = = ,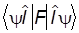

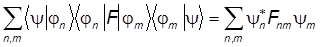т.е.

áFñ = 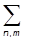F_nm y^*_n y_m.

 

Рассмотрим теперь другое представление, порожденное оператором :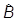

 

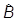| j^R _nñ = B_n| j^R _nñ, á j^R _n| j^R _mñ = d_nm, 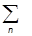| j^R _nñá j^R _n| = .

 

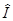Векторы |yñ в нем представляются другими волновыми функциями:

 

y^R_n = á j^R _n |yñ,

 

а операторы 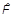- другими матрицами:

 

.

 

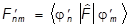Но так как оба базиса - ортонормированные, то волновые функции и матрицы операторов в обоих представлениях связаны унитарным преобразованием:

y^R_n = 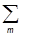U_nmy_m, F^R_nm = 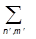U_nnRF_nRmRU⁺_mRm.

Раньше мы формулировали эти утверждения на языке операторов.

Найдем шпур (след) матрицы оператора 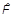в B -представлении:

 

 

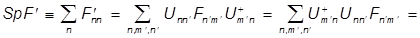
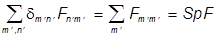= , (U⁺U = ),

 

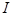т.е. шпур матрицы инвариантен относительно унитарного преобразования - не зависит от выбора представления.

Задача на собственные значения оператора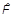

 

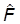|yñ = F|yñ

 

в матричном A-представлении ставится как

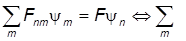(F_nm-Fd_nm)y_m = 0.

 

Система однородных линейных уравнений для определения y_m имеет нетривиальные решения при условии

 

det CF_nm-Fd_nmC = 0

 

Это вековое или характеристическое уравнение является алгебраическим. Его решения F₁,F₂,...F_k... есть искомые собственные значения. Подставляя каждое из них в систему уравнений, найдем последовательности

F₁: y⁽¹⁾_1, y⁽¹⁾_2,... y⁽¹⁾_n,..._..

 

F₂: y⁽²⁾₁, y⁽²⁾₂,... y⁽²⁾_n...

..............................................................

представляющие собственные векторы |y⁽ⁿ⁾ñ, т.е. являющиеся их волновыми функциями.

Если в качестве базисных векторов выбрать собственные векторы |y_n ñ оператора 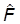, то его матрица будет диагональной:

 

F_nm = áy_n |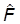|y_m ñ = áy_n |F_m|y_m ñ = F_m áy_n |y_m ñ = F_md_nm

 

Таким образом, решение задачи на собственные значения оператора 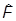равнозначна диагонализации его матрицы: находимUy_nñ, устанавливаем унитарное преобразование, связывающее Uy_nñ с Uj_nñ, и совершаем это унитарное преобразование над исходной матрицей F_nm. В результате и получим диагональную матрицу.

Все те же операции можно проделать и в случае, когда спектр оператора 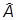- непрерывный, но все надо понимать в обобщенном смысле. Базис образуют обобщенные собственные векторы:

 

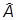|c_Añ = A|c_Añ, ác_A|c_Bñ = d(A-B), òdA|c_Añác_A| = .

 

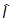Волновая функция

y (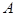)= ác_A|yñ

есть «настоящая» функция, ибо зависит от непрерывного аргумента. Если оператор 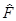переводит вектор |yñ в 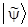, т.е.

 

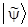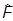= |yñ,

 

то для волновых функций имеем:

 

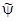(A) º ác_A|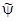ñ = ác_A|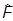|yñ = òác_A|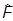|c_ARñ ác_AR|yñ,

т.е.

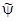(A) = òF(A,A^R)y(A^R)dA^R,

 

где

F(A,A^R) º ác_A|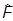|c_ARñ

 

ядро интегрального оператора .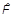

Для произведения двух операторов

 

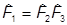
получим

F₁(A,A^R) = ác_A|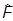₂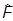₃ |c_ARñ = ác_A|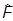₂|c_ARRñ ác_ARR|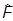₃|c_ARñ dA^RR,

 

т.е. ядро произведения получается как свертка операторов-сомножителей:

F(A,A^R) = ò F(A, A^RR) F(A^RR,A^R)dA^RR.

 

- . .- . - . - .

 

Рассмотрим уравнение Шредингера

 

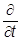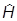ii|yñ = |yñ,

 

которое для одной частицы во внешнем поле записывается как

 

ii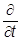|yñ = 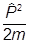|yñ +V(r)|yñ.

 

В координатном представлении мы его уже получали:

 

ii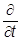y(r,t) = -i²/2m× Ñ² y(r,t) + 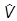(r) y(r,t).

 

Найдем теперь уравнение Шредингера в импульсном представлении. Нам нужно найти действие оператора 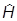, т.е. 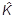= 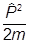и V(r) на волновую функцию 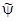(p), которая есть

 

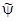(p) = ác_p|yñ.

 

Для ядра оператора V имеем

W(p,p^R) = ác_p|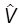|c_pRñ = (c_p(r),V(r)c_pR (r)),

 

где c_p(r) - собственные функции оператора импульса в координатном представлении:

c_p(r) = .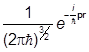

 

Подстановка дает:

W(p,p^R) = ,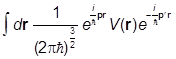

 

т.е. ядро W получается из V путем преобразования Фурье:

 

W(p,p^R) = .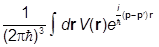

 

Для оператора кинетической энергии 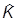имеем:

 

K(p,p^R) = - i²/2m×(c_p(r),Ѳc_p(r^R)) = - i²/2m×=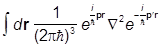

 

= - i²/2m× 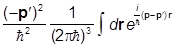= p²/2m×d(p-p^R):

 

K(p,p^R) = p²/2m×d(p-p^R).

 

Подставляем все это в уравнение Шредингера в импульсном представлении:

ii.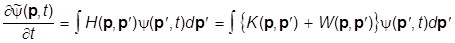

 

Получаем:

ii ,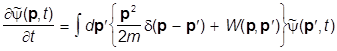

т.е.

ii ,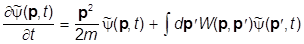

где

W(p,p^R) = .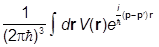

 

В итоге получилось интегро-дифференциальное уравнение.

Если V(r)есть полином от r²,т.е. включает сумму членов вида

 

V_n = a_nr²ⁿ,

 

то eсть уравнение Шредингера сводится к дифференциальному. Действительно, в этом случае

W_n(p,p^R) = =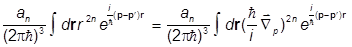

 

= a_n (-i²Ñ²_p )ⁿ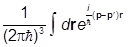= a_n(-i²Ñ²_p )ⁿd(p-p^R);

 

ò W_n(p,p^R) 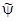(p^R,t)dp^R = a_n(-i²Ñ²_p )ⁿò d(p-p^R) 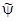(p^R,t)dp= a_n (-i²Ñ²_p )ⁿ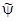(p,t);

 

ii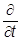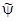(p,t) = (p² /2m +a_n(-i²Ñ²_p )ⁿ) 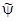(p,t).

 

Важный пример - изотропный гармонический осциллятор, с

 

V(r)=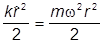(w² º k/m).

 

В координатном представлении уравнение Шредингера записывается как

ii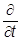y(r,t) = -i²/2m×Ѳ y(r,t) + (m w² r²/2)y(r,t).

 

В импульсном представлении, учитывая, что n = 1 и a = mw²/2, имеем:

 

ii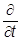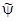(p,t) = p²/2m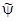(p,t) - i²mw²/2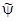Ѳ(p,t)

 

Уравнения с точностью до переобозначения констант идентичны, а значит идентичны и их решения. Но они, как функции в координатном и импульсном представлениях, должны быть связаны преобразованием Фурье. Поэтому, если не обращать внимания на константы, волновые функции изотропного гармонического осциллятора инвариантны относительно преобразования Фурье: сами функции и их фурье-образы практически совпадают. Таким свойством обладают функции Эрмита и только они, и мы предсказываем волновые функции стационарных состояний осциллятора.