ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

 

Классический осциллятор.

Пусть частица совершает одномерное движение. Разложим ее потенциальную энергию в ряд Тейлора в окрестности x = 0 до второго порядка:

V(x) = V(0) + 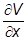|_x=0×x + 1/2 |×x².

 

Пусть x=0 - положение устойчивого равновесия. Тогда в этой точке V(x) - минимум, а потому

 

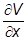(0) = 0, (0) º k>0.

 

Гамильтониан записывается как

 

H = p²/2m +kx²/2.

 

Он приводит к уравнению движения

,

с решением

x = Acos(wt + j).

 

Для энергии имеем

E = + kx²/2 =

 

= mw²A²/2×sin²wt + kA²/2×cos² wt = mw²A²/2.

 

Так как

,

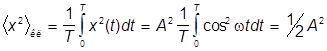то можно также записать

 

E = mw²á x²ñ_кл.

 

Квантовый осциллятор в координатном представлении

Гамильтониан имеет вид

 

²/2m + mw²x²/2),

и стационарное уравнение Шредингера записывается как

 

-i²/2m×y¢¢(x) + mw²x²/2×y (x) = Е×y (x).

 

К нему нужно добавить единственное граничное условие:

 

| y (x)| < +¥, (x ® ± ¥).

 

Вводя безразмерные координату y и энергию e:

 

y = x, e = 2E/iw,

 

переписываем уравнение (это тривиально):

 

(d²/dy² -y²+e) ×y(y) = 0.

 

Легко показать (отбрасывая член с ey(y)), что асимптотика решения такова:

y(x)+ B,

 

причем из граничного условия B=0. Поэтому, чтобы привести уравнение к стандартному виду, делаем замену неизвестной функции:

 

y(y) = U(y).

 

Для функции U(y) получается уравнение

 

U^RR- 2yU^R + (e-1)U = 0

 

с граничным условием

U(y) Þ 0 ( быстрее, чем возрастает ),.

 

Выписанное уравнение называется уравнением Эрмита. Так как y=0 - регулярная точка, решение можно искать в виде степенного ряда:

 

U(y) = .

 

Дифференцируем его и подставляем в уравнение:

 

{a_k(k-1)ky^k-2-a_k(2k+1-e)y^k} = 0,

или

{ a_k+2(k+1)(k+2)-a_k(2k+1-e)}y^k = 0,

откуда

a_k+2(k+1)(k+2)-a_k(2k+1-e) = 0,

 

и получаем рекуррентное соотношение для коэффициентов:

 

a_k+2 = {(2k+1-e)/(k+1)(k+2)} a^k.

 

Если ряд бесконечный, то при больших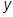

 

,

 

т.е. отношение соседних коэффициентов такое же, как в разложении

.

Это решение не удовлетворяет граничному условию. Поэтому ряд должен где-то оборваться. Тогда он будет конечным полиномом, из-за множителя функция Y(y) будет быстро убывать при y ® ±µ, и она будет квадратично интегрируемой.

Как же добиться того, чтобы U(y) было конечным полиномом?

Пусть

n = max{k} Û a_n¹0,a_n+2 = 0.

 

Тогда из рекуррентного соотношения

 

2n+1-e = 0.

 

Но этого еще не достаточно. Нужно еще потребовать, чтобы a_n+1=0.

Этот коэффициент выражается через a_n-1:

 

a_n+1 = {2(n-1)+1-e/n(n+1)} ×a_n-1.

 

Если бы числитель дроби равнялся нулю, то все было бы хорошо. Но в силу предыдущего

 

2(n-1)+1-e = [2n+1-e]-2 = -2 ¹ 0.

 

Поэтому нужно потребовать a_n-1=0, а также a_n-3=0, и так далее, пока не дойдем до a₀=0 или a₁=0. Ясно, что при n четном должно быть a₁=0, а при n нечетном - a₀=0, В любом случае условие обрыва ряда, т.е. превращения его в полином, имеет вид

 

2n+1-e = 0 Þ e = 2n +1,

 

откуда, вспоминая, что

,

получаем энергетический спектр гармонического осциллятора:

 

E_n = iw×(n+1/2), n = 0,1,2,...

 

Из предыдущего явствует, что если n четно, то a₁=0, и все =0, а потому волновая функция - четная:

 

Y_2k(-x) = +Y_2k(x).

 

Если же n-нечетно, то a₀=0, все a_2k=0, и волновая функция нечетна:

Y_2k+1(-x) = -Y_2k+1(x).

 

Если положить a₀=1, a₁=0 для одного набора решений и a₀=0, =1 для другого набора, то получим полиномы Эрмита:

 

.

Тогда волновые функции стационарных состояний будут функциями Эрмита:

,

 

где константы A_n следует определить из условия нормировки

 

Y|(y)|²dy = 1 или Y|(x)|²dx = 1.

 

Второе условие более физично, и оно окончательно дает

 

.