рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- ДРУГОЕ РЕШЕНИЕ ЗАДАЧИ О КВАНТОВОМ ОСЦИЛЛЯТОРЕ
Реферат Курсовая Конспект
ДРУГОЕ РЕШЕНИЕ ЗАДАЧИ О КВАНТОВОМ ОСЦИЛЛЯТОРЕ
ДРУГОЕ РЕШЕНИЕ ЗАДАЧИ О КВАНТОВОМ ОСЦИЛЛЯТОРЕ - раздел Механика, ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР Вернемся К Квантовому Осциллятору С Гамильтонианом ...
Вернемся к квантовому осциллятору с гамильтонианом
 +1/2mw2
+1/2mw2 2.
2.
Перепишем его, вводя вместо  и
и  новые операторы
новые операторы
 ,
,  ,
,
связанные друг с другом операцией сопряжения:
 ,
,  .
.
Из коммутационного соотношения
[ ,
, ] =
] = 


сразу следует, что
[ ] =
] =  ,
,
(это проверяется прямой подстановкой). Кроме того, выражая  и
и  через
через  и
и 
и подставляя результаты в  , получим
, получим
 =
= 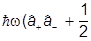
 ).
).
Отсюда элементарно проверяются коммутационные соотношения
[ ,
, ] =
] = 

 ; [
; [ ,
, ] = -
] = -

 .
.
Пусть yn- собственная функция  с собственным значением
с собственным значением  :
:
 yn = Enyn.
yn = Enyn.
Тогда
 yn
yn
или 0, или собственная функция  с собственным значением
с собственным значением  -
-
 . Действительно, используя коммутатор
. Действительно, используя коммутатор  с
с  , имеем:
, имеем:
 (
( yn) = (
yn) = (
 )yn = (
)yn = (
 -
-

 )yn =
)yn =
= ( En-
En-

 )yn = (En-
)yn = (En- 
 )(
)( yn).
yn).
Аналогично устанавливается второе утверждение. По этой причине  называется понижающим оператором, а
называется понижающим оператором, а  -повышающим оператором.
-повышающим оператором.
Но энергетический спектр осциллятора ограничен снизу - есть минимальная энергия E0, которой отвечает собственная функция y0 гамильтониана. Дальше понижать некуда, и должно быть
 y0 = 0.
y0 = 0.
Действуем на эту функцию гамильтонианом:
 y0 =
y0 = 
 (
(
 +
+ 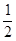
 )y0 = 0 +
)y0 = 0 + 

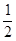
 y0 =
y0 = 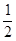

 y0.
y0.
Таким образом,
E0 = 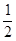

 .
.
Функция y0 есть волновая функция основного состояния (его называют также вакуумным состоянием). Она должна быть нормирована:
(y0, y0) = 1.
Действуя на нее последовательно оператором  , будем получать волновые функции новых стационарных состояний, повышая энергию каждый раз на
, будем получать волновые функции новых стационарных состояний, повышая энергию каждый раз на 
 . Придем к последовательности энергий
. Придем к последовательности энергий
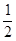

 ,
, 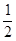

 +
+
 ,
, 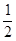

 + 2
+ 2 
 ,...
,...
т.е.
E0 = 
 (n+1/2).
(n+1/2).
Волновая функция стационарного состояния с En есть
yn = cn( +)ny0,
+)ny0,
где cn- нормировочные постоянные. Для таких функций
 yn = Enyn, En =
yn = Enyn, En = 
 (n+1/2).
(n+1/2).
Записывая
 yn =
yn = 
 (
(
 +1/2
+1/2 )yn = Enyn =
)yn = Enyn = 
 (n+1/2) yn,
(n+1/2) yn,
Получим
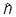 yn = nyn,
yn = nyn, 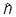 º
º 
 ,
,
т.е. спектр оператора 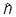 состоит из неотрицательных целых чисел 0,1,...
состоит из неотрицательных целых чисел 0,1,...
Терминология и физическая интерпретация таковы. Состояние с функцией yn «состоит» из остова (основного состояния) с энергией E0 = 1/2 
 и из n «квазичастиц» - квантов возбуждения с энергиями
и из n «квазичастиц» - квантов возбуждения с энергиями 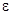 =
= 
 у каждого. Оператор
у каждого. Оператор  (часто обозначается просто
(часто обозначается просто 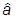 ) есть оператор уничтожения, а оператор
) есть оператор уничтожения, а оператор  (обозначение
(обозначение 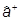 ) - оператор рождения квантов возбуждения ( квазичастиц ). Оператор
) - оператор рождения квантов возбуждения ( квазичастиц ). Оператор 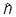 есть оператор числа квазичастиц (числа квантов возбуждения).
есть оператор числа квазичастиц (числа квантов возбуждения).
Естественные и довольно очевидные обобщения построенной схемы играют фундаментальную роль в статистической физике, физике твердого тела, квантовой теории поля и т.д., так как составляют основу метода вторичного квантования. Поэтому хорошо сформулировать данную схему на более абстрактном языке.
Представление чисел заполнения (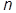 - представление, базис Фока)
- представление, базис Фока)
Отказываемся полностью от координатного представления, вводим через  и
и  операторы
операторы  и
и  с коммутационным соотношением
с коммутационным соотношением
[ ,
, ] =
] =  ,
,
записываем через них гамильтониан осциллятора
 =
= 
 (
(
 +1/2
+1/2 ) º
) º 
 (
(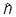 +1/2
+1/2 )
)
и выбираем в качестве базисных векторы
 ,
,
где
 |0ñ = 0,
|0ñ = 0,
а каждый |nñ - собственный вектор гамильтониана:
 |nñ = En|nñ, En =
|nñ = En|nñ, En = 
 (n +1/2).
(n +1/2).
Произвольный вектор состояния представляется разложением
|yñ =  yn|nñ
yn|nñ
и описывается волновой функцией (последовательностью) {yn} в n- представлении:
yn = án|yñ.
Смысл ее в том, что |yn |2есть вероятность того, что в состоянии y мы получим при измерении энергии значение En, т.е. обнаружим в этом состоянии n квантов возбуждения.
Имеют место следующие очень важные соотношения:
 |nñ =
|nñ =  |n+1ñ
|n+1ñ
и
 |nñ =
|nñ =  .
.
Первое проверяется непосредственно:
 |nñ =
|nñ = 
 º
º
 |n+1ñ.
|n+1ñ.
Второе доказываем по индукции. При n=0 оно выполняется в силу определения |0ñ. Допустим, что
 |n-1ñ =
|n-1ñ =  |n-2ñ.
|n-2ñ.
Тогда, используя только что доказанное и коммутатор [ ,
, ] =
] =  , имеем:
, имеем:
 |nñ =
|nñ = 
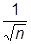
 |n-1ñ =
|n-1ñ =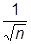 (
(
 )|n-1ñ =
)|n-1ñ = 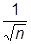 (
( +
+ 
 )|n-1ñ =
)|n-1ñ =
=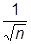 {|n-1ñ +
{|n-1ñ + |n-1ñ} =
|n-1ñ} = 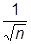 {|n-1ñ +
{|n-1ñ + |n-1ñ} =
|n-1ñ} = |n-1ñ,
|n-1ñ,
что и требовалось доказать. Теперь легко установить, что {|nñ} - базис ортонормированный:
ám|nñ = dmn.
Действительно, (m³n):
ám|nñ = á0| |n-1ñ =
|n-1ñ =
=  = dmn.
= dmn.
Как и всегда, в заданном представлении операторы представляются некоторыми матрицами - в данном случае
 ® Fmn = ám|
® Fmn = ám| |nñ.
|nñ.
Зная действие операторов  - и
- и  + на |nñ, сразу находим их матрицы:
+ на |nñ, сразу находим их матрицы:
ám| -|nñ =
-|nñ =  ám|n-1ñ =
ám|n-1ñ =  dm,n-1
dm,n-1
и
ám| +|nñ =
+|nñ =  ám|n+1ñ =
ám|n+1ñ =  dm,n+1,
dm,n+1,
т.е.
( m)mn =
m)mn =  dm,n-1, (
dm,n-1, ( +)mn =
+)mn =  dm,n+1
dm,n+1
Еще проще матрица оператора числа квантов возбуждения:
ám|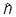 |nñ = nám|nñ = ndm,n.
|nñ = nám|nñ = ndm,n.
Как и положено быть матрице оператора в собственном представлении, она диагональна:
(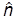 )mn = ndm,n.
)mn = ndm,n.
В явном виде
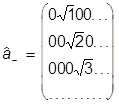 ,
,  ,
,  .
.
Напомним, что векторы состояний представляются матрицами-столбцами:
 ...
...
От n- представления легко перейти в 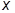 - представление и найти волновые функции в явном виде. Основное условие
- представление и найти волновые функции в явном виде. Основное условие
 -|0ñ = 0
-|0ñ = 0
в координатном представлении записывается как
 )y0(x) = 0;
)y0(x) = 0;  = x,
= x,  =
=  ,
,
или, переходя к безразмерной координате y=x/x0,
(y+ )y0(y) = 0.
)y0(y) = 0.
Общее решение этого уравнения очевидно:
y0(y) = C0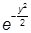 .
.
Константу C0 находим из условия нормировки:
1 = (y0, y0) = =
=
=C2x0 ,
,
так что
y0(y) =  .
.
Для волновой функции n-го стационарного состояния имеем:

Но это и есть функция Эрмита. Действительно, учитывая, что
 ,
,
и полагая
f(y) = ,
,
придем к функциям Эрмита в форме Родрига
 ,
,
которые уже были выписаны (но не получены!) в начале лекции.
– Конец работы –
Эта тема принадлежит разделу:
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
СРАВНЕНИЕ КВАНТОВОГО И КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРОВ... Вернемся к квантовому осциллятору и сравним его поведение с поведением классического осциллятора...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ДРУГОЕ РЕШЕНИЕ ЗАДАЧИ О КВАНТОВОМ ОСЦИЛЛЯТОРЕ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов