Глава 5. Колебания. Волны
Глава 5. Колебания. Волны
Колебания. Дифференциальное уравнение гармонических колебаний. Кинематическое уравнение гармонического колебания. Амплитуда, фаза, частота, период колебаний
|
Колебаниями называются процессы, отличающиеся определенной степенью повторяемости (например: качание маятника, колебания струны, изменение тока в колебательном контуре и т.п.).
Свободными или собственными колебаниями называют такие колебания, которые происходят в системе, представленной самой себе, после того как ее вывели из положения равновесия.
При вынужденных колебаниях на систему действует внешняя периодически меняющаяся сила. Частный случай вынужденных колебаний - автоколебания: моменты действия вынуждающей силы задает сама система.
В § 16 было показано, что вблизи положения равновесия, т.е. минимума потенциальной энергии, движение частицы имеет колебательный характер. Вберем нулевой уровень отсчета 
и начало координат так, что бы минимум 
и соответствовал точке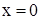 
(рис.17.1).
Вблизи минимума, т.е. при достаточно малых x, любая функция 
имеет вид параболы. Следовательно, для достаточно малых x
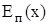~x2 (17.1)
Если выполняется условие (17.1), движение называют малыми колебаниями. Обозначим коэффициент пропорциональности в соотношении (17.1) k/2, где “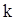
” некоторая постоянная. Тогда
(17.2)
Из уравнения (13.3) получим:
(17.3)
Следовательно, вблизи минимума потенциальной энергии на частицу действует такая же сила, как сила упругости (уравнение (5.3)). Ее называют квазиупругой силой.
Запишем второй закон Ньютона:
. Т.к. 
то 
(17.4)
Величина 
; обозначим ее 
:
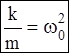(17.5)
Подставим (17.5) в (17.4):
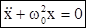(17.6)
Уравнение (17.6) называется дифференциальным уравнением гармонических колебаний. Решением дифференциального уравнения (17.6) являются функции, имеющие вид:
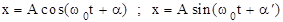(17.7а)
где A,
- некоторые константы (то, что (17.7а) решение (17.6) можно проверить непосредственной подстановкой). Уравнения (17.7а) называются кинематическим уравнением гармонических незатухающих колебаний. (Отметим, что рассматриваемые колебания являются собственными)
Поскольку cosj = sin(j - p/2), то от первого уравнения (17.7а) всегда можно перейти ко второму и наоборот. В дальнейшем, для определенности, будем использовать первое из уравнений (17.7а):
(17.7)
В уравнении (17.7) x- величина отклонения от положения равновесия; 
- называется циклической частотой;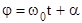 
- называется фазой колебания (измеряется в радианах); при t = 0 j = a, a - называется начальной фазой. Т.к. максимальное значение cosj = 1, то из (17.7) получим модуль максимального значения отклонения от положения равновесия 
:
  
       
|
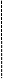
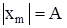
Величина А - называется амплитудой колебания. На рис.(17.2) показан график гармонических колебаний (т.е. график уравнения (17.7)).
Промежуток времени T, разделяющий два положения, у которых фаза отличается на 2 p называется период колебания (рис 17.2). Другими словами период - это время одного полного колебания. Из определения T получим:
;
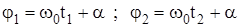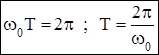(17.8)
Величина обратная периоду называется частотой колебания 
(17.9)
Из ур-ий (17.8), (17.9) получим единицы измерения величин T и n:
; 
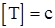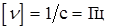(Герц)