ЭЛЕКТРОН В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

 

Рассмотрим движение дираковской частицы с S=1/2 в электростатическом поле с точностью до членов порядка v²/c². Исходим из точной системы уравнений для двухкомпонентных спиноров j и c:

y =:

(Е-еА₀)j = Сsc

(Е+2mc² - еА ₀)c = Сs j

 

и полагаем в нем А = 0, еА₀ = V(r) - потенциальная энергия частицы в электростатическом поле:

 

(Е-V)j = С(sр)c

(Е + 2mc² - V)c = С(sр)j

 

Выражаем из второго c и разлагаем в ряд до первого члена:

c

Подставляем в первое уравнение:

(Е -V)j = (sр) j.

Для преобразования правой части используем прежде всего коммутационное соотношение

 

,

 

а затем действуем примерно так же, как в предыдущей лекции:

 

(sр)f(r)(sр)=f(r)(sр)(sр)-is(sр) =

 

 

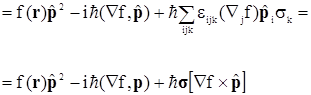
С учетом этого, уравнение переписывается как

 

(E -V)j = .

 

Разберемся с условием нормировки. Исходно оно записывается как

 

.

 

Учитывая, что

,

получим

,

 

или, подставляя сюда совсем приближенное выражение для c через j :

 

найдем

 

Видно, что для избавления от неприятного множителя удобно ввести новую функцию f:

 

где второе равенство получено в используемом приближении. В том же приближении для новой функции условие нормировки запишется обычно:

.

 

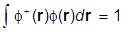Подставляем j через f в переписанное уравнение, представим его (с той же точностью) в виде стационарного уравнения Шредингера:

 

.

 

Разберемся, что же мы получили. Уравнение имеет вид

f=Ef,

 

где гамильтониан равен

Член

+V

есть обычный нерелятивистский гамильтониан. Рассматриваем член

.

 

Учтем, что Е - «обычная» энергия, а значит Е+mc² - полная релятивистская энергия, а значит (Е+mc²)-V - релятивистская «кинетическая» энергия (включающая и энергию покоя). Она обычным образом связана с импульсом, и можно записать

.

 

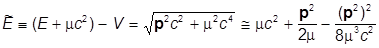Таким образом, - просто следующая поправка к обычной кинетической энергии. Так как в нулевом приближении

Е -V = Þ p² = 2m(E-V),

 

то можно записать также

.

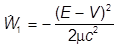Член

 

называется дарвиновской поправкой - это есть релятивистская поправка к потенциальной энергии. Третий член

 

называется спин-орбитальным взаимодействием. Причина этому следующая. Пусть V=V(r), т.е. электрическое поле - центральное. Тогда

ÑV(r) = .

 

Тогда, подставляя это в и учитывая, что

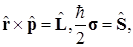
получим

,

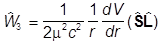откуда и название.

Рассмотрим теперь водородоподобный атом, когда

.

 

Стационарное уравнение Шредингера (с поправками) записывается как

.

Здесь

,

причем

,

 

,

 

.

 

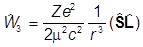Полезно ввести полный момент электрона

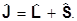
Возводя в квадрат, получим

,

так что

 

Кроме того, запишем ₀ в сферических координатах:

.

 

Имея полный гамильтониан, легко убедиться, что он коммутирует с При этом не входит в уравнение, а потому по проекции полного момента будет вырождение. Энергетические уровни будут характеризоваться собственными значениями трех первых операторов, т.е. квантовыми числами Е, , j (S можно не писать, ибо оно раз и навсегда фиксировано и равно 1/2). Волновые функции стационарных состояний будут собственными функциями для и потому в гамильтониане эти операторы можно заменить их собственными значениями, равными соответственно

l(l+1), 3/4, j(j+1).

 

В рассматриваемых состояниях угловая и спиновая зависимости волновых функций нам известны - они были выписаны в теории сложения моментов:

 

Но явный вид даже не важен. Важно, что все моменты действуют только на углы и спины, «вышибая» при этом соответствующие собственные значения. Поэтому, подставляя данную волновую функцию в уравнение Шредингера, получим для радиальной волновой функции уравнение

 

Здесь W₁ и W₂ приведены выше, а вместо W₃ теперь следует писать

 

 

Уравнение можно переписать так:

 

и искать его решения по теории возмущений. Однако здесь есть хитрость - нужно применять теорию возмущений на вырожденном уровне, а не хочется. Но все будет хорошо, если мы сразу выберем правильные волновые функции нулевого приближения - с теми же квантовыми числами, что в точных состояниях. Ими являются

,

где радиальная функция подчиняется водородному уравнению

,

из которого

E_n = -, n =1, 2,...

 

Тогда в секулярном уравнении все недиагональные матричные элементы обратятся в нуль, и для поправок к энергии первого порядка получим формально те же формулы, что и в теории возмущений на невырожденном уровне. Они будут задаваться средними значениями возмущения по соответствующим невозмущенным состояниям:

DE_nlj =.

 

Это можно получить и непосредственно. Записываем точные решения в виде (индексы для краткости опускаем):

Е = Е₀ + DЕ, f = f₀ + Df,

и подставляем в уравнение:

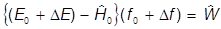(f₀+Df).

Раскрываем

,

 

здесь первое и третье слагаемые в сумме равны нулю в силу нулевого уравнения Шредингера

E₀f₀ - 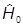f₀ = 0,

 

а слагаемые, включающие DЕDf и WDf, являются членами второго порядка малости, которые мы не учитываем.

 

 

Остается

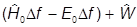DEf₀ = f₀,

 

и, замечая, что

(f₀,f₀) = 1; f₀, Df) = E₀(f₀, Df), (f₀,E₀Df) = E₀(f₀, Df),

 

получим после скалярного умножения на f₀ слева

DE = ,

 

а отсюда и требуемый результат.

Итак, поправка в первом порядке теории возмущений есть

 

DE_nlj = r²dr.

 

При вычислениях интегралов удобно перейти к атомным единицам

 

и ввести постоянную тонкой структуры

a º » 1/137.

Тогда можно записать

D_nlj = I₁ + I₂ + I₃,

 

где I_k - соответствующие интегралы от W_k, и вычислить:

;

;

 

Во втором члене получился 0 при 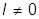потому, что f⁰»r^l при r ®0, а интегрируется дельта-функция.

Собирая все поправки вместе, а также переходя к обычным единицам энергии, получим в первом порядке теории возмущений

E_nj @ E_n⁽⁰⁾ + DE_nj = -.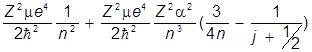

 

Видим, что теперь энергетические уровни помимо главного квантового числа n зависят также от полного момента j. В нулевом приближении уровни были 2n² - кратно вырождены (без учета спина n² - кратно), а теперь вырождение в значительной степени снято. Но все-таки немножко осталось, так как в энергию не входит . И пары уровней, имеющие одинаковые n и j при , остаются вырожденными. К тому же есть вырождение и по m_j - по проекции полного момента (это в силу изотропии пространства) - оно, как и всегда, (2j +1) - кратное. Последнее вырождение снимается при учете спина ядра, который взаимодействует со спином электрона - это есть сверхтонкое расщепление, а то, что мы получили, именуется тонким расщеплением (почему a и называется постоянной тонкой структуры). Интересно, что при точном решении уравнения Дирака двукратное вырождение при все равно остается. И только при учете взаимодействия электрона с вакуумом оно снимается - возникает так называемый лэмбовский сдвиг, открытый Лэмбом и Ризерфордом (именно «и»!) в 1947 г. Его объяснила квантовая электродинамика, с чего и начинается ее современная история. Именно на этом эффекте (и на аномальном магнитном моменте электрона - см. чуть выше) была отработана процедурой перенормировок, о которой говорилось в связи с силой радиационного трения и проблемой полевой массы электрона.