СОСТОЯНИЯ МИКРОСИСТЕМ
Л Е К Ц И Я 2
СОСТОЯНИЯ МИКРОСИСТЕМ.
ПОСТУЛАТЫ КВАНТОВОЙ МЕХАНИКИ
Продолжение
Согласно принципу, если система может находиться в состояниях y1 и y2, то она может находиться и в состоянии y, описываемом вектором |yñ = с1|y1ñ +с2|y2ñ , с1, с2 Î C.Постулат II. Если векторы |yñ и |jñ нормированы, и система находится в состоянии y, то вероятность обнаружить ее в состоянии j равна |áj|yñ|2.
Для векторов гильбертова пространства справедливо неравенство Коши - Буняковского (оно же Шварца)
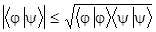 .
.
Отсюда следует, что для вероятностей
0 £ |áj|yñ|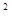 £ 1,
£ 1,
как это и должно быть.
Замечание. Если векторы 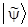 и
и  состояний y и j ненормированы, то их всегда можно сделать таковыми, умножая на подходящие числа:
состояний y и j ненормированы, то их всегда можно сделать таковыми, умножая на подходящие числа:
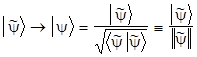 .
.
Поэтому в общем случае указанная вероятность вычисляется так:
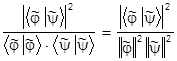
Постулат III. Каждой динамической переменной (наблюдаемой) соответствует некоторый линейный оператор , который действует в пространстве векторов состояния, и который является самосопряженным (эрмитовым): + = .
Вспомним некоторые математические понятия. Для линейного оператора
 {c1|y1ñ + c2|y2ñ} = c1
{c1|y1ñ + c2|y2ñ} = c1 |y1ñ + c2
|y1ñ + c2 |y2ñ;
|y2ñ;
"|y2ñ,|y2ñ Î c2, c1 Î C.
В множестве операторов вводятся операции сложения:
def
( 1+
1+ 2)|yñ =
2)|yñ =  1|yñ +
1|yñ +  2|yñ,
2|yñ,
умножения на комплексные числа:
def
(с )|yñ = с (
)|yñ = с ( |yñ)
|yñ)
и перемножения:
def
( 1
1 2)|yñ =
2)|yñ =  1 (
1 ( 2|yñ).
2|yñ).
Операция умножения операторов, вообще говоря, некоммутативна:

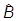 ¹
¹ 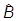
 .
.
В связи с этим вводится понятие коммутатора двух операторов:
[ ,
,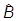 ] =
] =
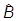 –
– 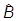
 .
.
Оператор  +называется сопряженным к оператору
+называется сопряженным к оператору  , если
, если
( y1,  +y2) = (
+y2) = ( y1,y2), " y1,y2 Î
y1,y2), " y1,y2 Î 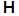 .
.
Это в обычных обозначениях, принятых математиками. Перейдем к обозначениям Дирака, где y º |yñ:
( y1,  y2) º áy1U
y2) º áy1U y2ñ º áy1U
y2ñ º áy1U Uy2ñ.
Uy2ñ.
Операцию сопряжения можно ввести и для векторов: по определению
(|yñ)+= áy|, (áy1U)+ = |yñ, а для чисел она понимается просто как комплексное сопряжение. Для скалярного произведения (числа) имеем, применяя…Постулат V. Результатом измерения наблюдаемой A может быть только значение, принадлежащее спектру соответствующего ей оператора.
Введем важное понятие дисперсии наблюдаемой А в состоянии y:
Dy(A) º á(DA)2ñ º áy|( -á
-á ñ)
ñ)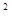 |yñ.
|yñ.
Раскрывая скобки, получим:
Dy(A) = áy| 2|yñ - 2á
2|yñ - 2á ñáy|
ñáy| |yñ + á
|yñ + á ñ2áy|yñ = á
ñ2áy|yñ = á 2ñ-2á
2ñ-2á ñ2+á
ñ2+á ñ2,
ñ2,
т.е.
Dy(A) = á 2ñ - á
2ñ - á ñ2.
ñ2.
Если |yñ - собственный вектор оператора  (
( |yñ = A|yñ), то дисперсия величины A в состоянии y равна нулю:
|yñ = A|yñ), то дисперсия величины A в состоянии y равна нулю:
 |yñ = A|yñ Þ Dy(A) = 0.
|yñ = A|yñ Þ Dy(A) = 0.
Это сразу следует из последнего представления Dy(A) как
á 2ñ - á
2ñ - á ñ2.
ñ2.
Таким образом, можно говорить, что наблюдаемая A в собственном состоянии y имеет строго определенное значение - равное собственному значению A.
Вычислим теперь среднее значение A в произвольном состоянии, для чего разложим его по собственным векторам оператора  :
:
|yñ =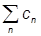 |jnñ +
|jnñ +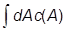 |cAñ,
|cAñ,
áy| = 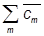 ájn| +
ájn| +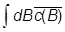 ácB|;
ácB|;
á ñ = áy|
ñ = áy| |yñ =
|yñ =
= 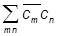 ájm|
ájm| |jnñ +
|jnñ + 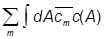 ájm
ájm |cAñ +
|cAñ +
+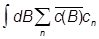 ácB|
ácB| |jnñ +
|jnñ + ácB|
ácB| |cAñ =
|cAñ =
= 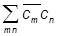 Andmn+ 0 + 0 +
Andmn+ 0 + 0 + Ad(B-A):
Ad(B-A):
á ñ =
ñ = 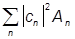 +
+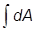 |c(A)|2A.
|c(A)|2A.
Отсюда и из элементарной теории вероятностей сразу видно, что
|cn|2- вероятность в состоянии y получить значение An,
|c(A)|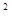 - плотность вероятности в состоянии y получить значение A.
- плотность вероятности в состоянии y получить значение A.
Пусть теперь  - эрмитов оператор, спектр которого дискретный и невырожденный. Тогда все собственные векторы
- эрмитов оператор, спектр которого дискретный и невырожденный. Тогда все собственные векторы
 |jlñ = Al|jlñ
|jlñ = Al|jlñ
лежат в H и автоматически ортогональны:
áj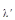 |j
|j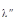 ñ =
ñ = 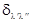 .
.
Таким образом, {|jlñ} есть ортонормированный базис в H. Разложим по нему произвольный вектор |yñ:
|yñ = 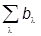 |jlñ.
|jlñ.
Для отыскания коэффициентов разложения умножим слева на áj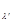 |:
|:
áj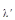 |yñ =
|yñ = 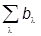 áj
áj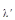 |jlñ =
|jlñ =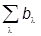
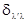 =
= 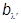 ,
,
откуда
bl = ájl|yñ,
и
|yñ = 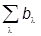 |jlñ =
|jlñ = 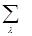 |jlñájl|yñ.
|jlñájl|yñ.
При наличии вырождения векторы |jlñ не будут однозначно определяться своими собственными значениями Al. И необходимо вместе с A ввести еще одну величину B с оператором 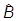 - так, чтобы собственные векторы Uj lñ оператора
- так, чтобы собственные векторы Uj lñ оператора  были бы собственными векторами и оператора
были бы собственными векторами и оператора 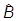 . Для последнего они будут иметь свои собственные значения Bn , и каждый вектор будет нумероваться двумя индексами - l и n:
. Для последнего они будут иметь свои собственные значения Bn , и каждый вектор будет нумероваться двумя индексами - l и n:
 |jlnñ = Al|j lnñ,
|jlnñ = Al|j lnñ, 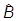 |j lnñ = Bn|j lnñ.
|j lnñ = Bn|j lnñ.
Если теперь нет общего вырождения, т.е. паре чисел l и n, а фактически Al и Bn, отвечает один вектор |jlnñ, то процедура закончена. В противном случае нужно ввести еще одну величину C с оператором 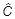 - так, чтобы старые собственные векторы операторов
- так, чтобы старые собственные векторы операторов  и
и 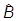 были бы собственными векторами
были бы собственными векторами 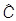 , и так далее.
, и так далее.
Для того, чтобы оператор 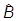 обладал указанным свойством, необходимо, чтобы он коммутировал с оператором
обладал указанным свойством, необходимо, чтобы он коммутировал с оператором  :
:
[ ,
,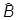 ] = 0.
] = 0.
Действительно, имеем:
[ ,
,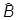 ]|yñ = (
]|yñ = (
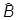 -
-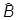
 )|yñ =
)|yñ =
= (
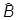 -
-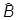
 )
)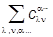 |ja...lnñ =
|ja...lnñ =
= (
(
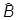 -
-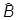
 )|j
)|j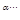
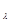
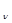 ñ =
ñ =
= (
(
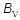 -
-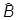
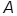
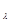 )|j
)|j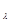
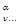 ñ =
ñ =
=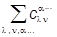 (AlBn - Bn Al|jaln...ñ = 0,
(AlBn - Bn Al|jaln...ñ = 0,
откуда, в силу произвольности вектора |yñ, [ ,
,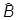 ] = 0.
] = 0.
Имеет место следующее полезное свойство:
[ ,
,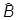 ] = 0 Þ (
] = 0 Þ (
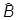 )+=
)+=
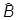 .
.
Действительно,
(
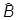 )+ =
)+ = 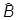 +
+ + =
+ = 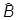
 =
= 
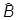 .
.
Определение. Набор независимых наблюдаемых называется полным, если все их операторы коммутируют, и если он не может быть расширен.
Смысл названия выявляет описанная выше процедура. У операторов полного набора есть собственные векторы, общие для них, которые образуют базис в H, и совокупный спектр которых является невырожденным (простым). Это означает, что каждому множеству индексов l,n,..., т.е. каждой совокупности собственных значений Al,Bn ,...отвечает только один вектор |jln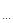 ñ.
ñ.
Вернемся к оператору , спектр которого дискретный и простой. (В общем случае под
, спектр которого дискретный и простой. (В общем случае под  можно понимать весь полный набор, а под n - весь набор индексов, однозначно задающих общие собственные векторы). Поставим задачу на собственные значения
можно понимать весь полный набор, а под n - весь набор индексов, однозначно задающих общие собственные векторы). Поставим задачу на собственные значения
 |jnñ = An|jnñ,
|jnñ = An|jnñ,
разложим произвольный вектор |yñ по базису {|jnñ}
|yñ = 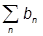 |jnñ =
|jnñ = 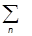 |jnñájn|yñ
|jnñájn|yñ
и подействуем на |yñ оператором :
:
 |yñ =
|yñ = 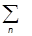
 |jnñájn|yñ =
|jnñájn|yñ = 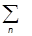 An|jnñájn|yñ,
An|jnñájn|yñ,
т.е.
 |yñ =
|yñ = 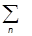 An|jnñájn|yñ.
An|jnñájn|yñ.
По определению, функция F( ) от оператора
) от оператора  определяется так:
определяется так:
F( )|yñ º
)|yñ º 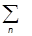 F (An)|jn ñájn|yñ,
F (An)|jn ñájn|yñ,
откуда
F( ) =
) = 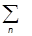 F (An)|jnñájn|.
F (An)|jnñájn|.
Полагая  =
= 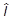 , где
, где 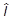 - единичный оператор, получим формулу разложения единицы:
- единичный оператор, получим формулу разложения единицы:
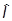 =
= 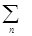 |jnñájn|.
|jnñájn|.
Обозначим каждое слагаемое:
Pn º |jnñájn|
и выясним его смысл, для чего подействуем на произвольный |yñÎH:
Pn|yñ = |jnñájn|yñ,
но ájn|yñ - есть коэффициент разложения |yñ по {|jnñ}:
ájn|yñ = bn,
а потому
Pn|yñ = bn|jnñ.
Таким образом, оператор Pn сопоставляет каждому вектору |yñ его проекцию на базисный орт |jnñ, т.е. Pn есть оператор проектирования на |yñ, или просто проектор.
Обобщение на случай смешанного спектра очевидно:
F(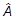 ) =
) = 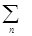 F (An)|jnñájn| + òdAF(A)|cAñácA|,
F (An)|jnñájn| + òdAF(A)|cAñácA|,
и формула разложения единицы принимает вид
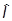 =
= 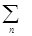 |jnñájn| + òdA|cAñácA|.
|jnñájn| + òdA|cAñácA|.
Прежде чем двигаться дальше, необходимо кратко резюмировать основные положения квантовой механики, которые были сформулированы выше.
РЕЗЮМЕ
Постулат 1. Состояния квантовомеханической системы описываются нормированными векторами |yñ гильбертова пространства H:
Yñ ÎH: =1.
Если вектор |yñ не нормирован, то его можно сделать таким:
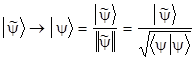 .
.
Принцип суперпозиции. Если система может находиться в состояниях y1 и y2, то она может находиться и в любом состоянии y с вектором
|yñ = c1|y1ñ + c2|y2ñ, 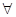 c1,c2
c1,c2 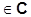 .
.
Постулат II. Если векторы |yñ и |j ñ нормированы, и система находится в состоянии y, то вероятность обнаружить ее в состоянии j равна |áj|yñ|2.
Постулат III. Каждой динамической переменной (наблюдаемой) 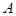 соответствует некоторый эрмитов оператор
соответствует некоторый эрмитов оператор  =
= 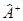 .
.
Важнейшую роль играет задача на собственные значения
 |jA ñ = A|jAñ.
|jA ñ = A|jAñ.
Если |jA ñ Î H, то собственный вектор - обычный, если |jA ñ Ï H, то он обобщенный. Обычные собственные значения образуют дискретный спектр, обобщенные - непрерывный спектр, совокупность тех и других образует полный спектр оператора  . Если данному собственному значению отвечает один (с точностью до множителя) собственный вектор, то оно невырожденное, или простое; в противном случае собственное значение вырожденное, или кратное.
. Если данному собственному значению отвечает один (с точностью до множителя) собственный вектор, то оно невырожденное, или простое; в противном случае собственное значение вырожденное, или кратное.
Собственные значения эрмитова оператора вещественны. Собственные векторы, отвечающие разным собственным значениям, ортогональны. Собственные векторы, отвечающие данному вырожденному собственному значению, автоматически не ортогональны, но если они линейно независимы, то их всегда можно сделать взаимно ортогональными. Таким образом,
ájn|jmñ = dnm для дискретного спектра,
ájn|cAñ = 0,
ácA|c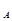 ¢ñ = d(A-A’)для непрерывного спектра.
¢ñ = d(A-A’)для непрерывного спектра.
Совокупность всех собственных векторов {|jA ñ} эрмитова оператора  образует базис в H, т.е. по ним можно разложить любой вектор |yñ Î H:
образует базис в H, т.е. по ним можно разложить любой вектор |yñ Î H:
|yñ = 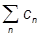 |jnñ + òdAC(A)|cA ñ.
|jnñ + òdAC(A)|cA ñ.