рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Приборостроение
- /
- Вероятностный подход к описанию погрешностей
Реферат Курсовая Конспект
Вероятностный подход к описанию погрешностей
Вероятностный подход к описанию погрешностей - раздел Приборостроение, МЕТРОЛОГИЯ Законы Распределения Случайных Погрешностей. Случайные Погрешности Обн...
Законы распределения случайных погрешностей. Случайные погрешности обнаруживают при проведении ряда измерений одной и той же величины. Результаты измерений при этом, как правило, не совпадают между собой, так как из-за суммарного воздействия множества различных факторов, не поддающихся учету, каждое новое измерение дает и новое случайное значение измеряемой величины. При правильном проведении измерений, достаточном их числе и исключении систематических погрешностей и промахов можно утверждать, что истинное значение измеряемой величины не выходит за пределы значений, полученных при этих измерениях. Оно остается неизвестным до тех пор пока не определено теоретически вероятное значение случайной погрешности.
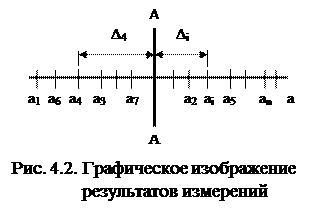
Пусть величину А измеряли п раз и наблюдали при этом значения а1, a2, а3,…,аi,...,аn. Случайная абсолютная погрешность единичного измерения определяется разностью
Di = ai – A . (4.1)
Графически результаты отдельных измерений представлены на рис. 4.2.
При достаточно большом числе п одни и те же погрешности, если они имеют ряд дискретных значений, повторяются и поэтому можно установить относительную частоту (частость) их появления, т.е. отношение числа полученных одинаковых данных mi к общему числу проведенных измерении п. При продолжении измерений величины А эта частота не изменится, поэтому ее можно считать вероятностью появления погрешности при данных измерениях: p(Ai) = mi / n.
 Статистическая зависимость вероятности появления случайных погрешностей от их значения называется законом распределе- ния погрешностей или законом распределения вероятности. Этот закон определяет характер появления различных результатов отдельных измерений. Различают два вида описания законов распределения: интегральный и дифференциальный.
Статистическая зависимость вероятности появления случайных погрешностей от их значения называется законом распределе- ния погрешностей или законом распределения вероятности. Этот закон определяет характер появления различных результатов отдельных измерений. Различают два вида описания законов распределения: интегральный и дифференциальный.
Интегральным законом, или функцией распределения вероятностей F(D) случайной погрешности Di в i-м опыте, называют функцию, значение которой для каждого D является вероятностью события Р(D), заключающегося в том, что случайная погрешность Di принимает значения, меньше некоторого значения D, т.е. функцию F(D) = Р[Di < D]. Эта функция при изменении D от -¥ до +¥ принимает значения от 0 до 1 и является неубывающей. Она существует для всех случайных величин как дискретных, так и непрерывных (рис 4.3 а).
Если F(D) симметрична относительно точки А, соответствующей вероятности 0,5 , то распределение результатов наблюдения будет симметрично относительно истинного значения А. В этом случае целесообразно F(D) сдвинуть по оси абсцисс на значение DA, т.е. исключить систематическую составляющую погрешность (DА = Dс) и получить функцию распределения случайной составляющей погрешности D = 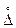 (рис. 4.3 б). Функция распределения вероятности погрешности D отличается от функции распределения вероятности случайной составляющей погрешности только сдвигом по оси абсцисс на значение систематической составляющей погрешности Dс .
(рис. 4.3 б). Функция распределения вероятности погрешности D отличается от функции распределения вероятности случайной составляющей погрешности только сдвигом по оси абсцисс на значение систематической составляющей погрешности Dс .
Дифференциальным законом распределения вероятностей для случайной погрешности с непрерывной и дифференцируемой функцией распределения F(D) называют функцию 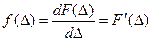 . Эта зависимость есть плотность распределения вероятностей. График плотности распределения вероятностей может иметь различную форму в зависимости от закона распределения погрешностей. Для F(D), изображенной на рис. 4.3 б, кривая распределения f(D) имеет форму, близкую к форме колокола (рис. 4.3 в).
. Эта зависимость есть плотность распределения вероятностей. График плотности распределения вероятностей может иметь различную форму в зависимости от закона распределения погрешностей. Для F(D), изображенной на рис. 4.3 б, кривая распределения f(D) имеет форму, близкую к форме колокола (рис. 4.3 в).
Вероятность появления случайных погрешностей определяется площадью, ограниченной кривой f(D) или её частью и осью абсцисс (рис. 4.3 в). В зависи мости от рассматриваемого интервала погрешности  .
.

Значение f(D)dD есть элемент вероятности, равный площади прямоугольника с основанием dD и абсциссами D1 , D2, называемыми квантилями. Так как F(+¥)=1, то справедливо равенство 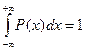 ,
,
т.е. площадь под кривой f(D) согласно правилу нормирования равна единице и отражает вероятность всех возможных событий.
В практике электрических измерений одним из наиболее распространенных законов распределения случайных погрешностей является нормальный закон (Гаусса).
Математическое выражение нормального закона имеет вид
 ,
,
где f(D) – плотность вероятности случайной погрешности D = аi - A; s - среднее квадратическое отклонение. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдений Di (см. формулу (4.1)):
 .
.
Характер кривых, описанных этим уравнением для двух значений s, показан на рис. 4.4. Из этих кривых видно, что чем меньше s, тем чаще встречаются малые случайные погрешности, т.е. тем точнее выполнены измерения. В практике измерений встречаются и другие законы распределения, которые могут быть установлены на основании статистической обработки
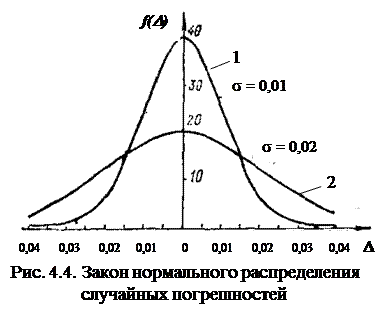 опытных данных. Некоторые из наиболее часто встречающихся законов распределения приведены в ГОСТ 8.011-84 «Показатели точности измерений и формы представления результатов измерений».
опытных данных. Некоторые из наиболее часто встречающихся законов распределения приведены в ГОСТ 8.011-84 «Показатели точности измерений и формы представления результатов измерений».
Основными характеристи- ками законов распределения являются математическое ожидание и дисперсия.
Математическое ожидание случайной величины - это такое ее значение, вокруг которого группируются результаты отдельных наблюдений. Мате-матическое ожидание дискрет-ной случайной величины М[X] определяется как сумма произ-ведений всех возможных значений случайной величины на вероятность этих значений 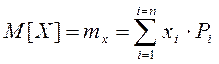 .
.
Для непрерывных случайных величин приходится прибегать к интегрированию, для чего необходимо знать зависимость плотности вероятности от х , т. е. f(х), где х=D. Тогда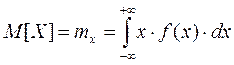 .
.
Это выражение означает, что математическое ожидание равно сумме бесконечно большого числа произведений всех возможных значений случайной величины х на бесконечно малые площади f(х)dх, где f(х) —ординаты для каждого х, a dх - элементарные отрезки оси абсцисс.
Если наблюдается нормальное распределение случайных погрешностей, то математическое ожидание случайной погрешности равно нулю (рис. 4.4). Если же рассматривать нормальное распределение результатов, то математическое ожидание будет соответствовать истинному значению измеряемой величины, которое мы обозначаем через A.
Систематическая погрешность при этом представляет собой отклонение математического ожидания результатов наблюдений от истинного значения А измеряемой величины: Dс = М[X] – A, а случайная погрешность – разность между результатом единичного наблюдения и математическим ожиданием: 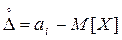 .
.
Дисперсия ряда наблюдений характеризует степень рассеивания (разброса) результатов отдельных наблюдений вокруг математического ожидания:
D[X] =Dx=M[(ai – mx)2].
Чем меньше дисперсия, тем меньше разброс отдельных результатов, тем точнее выполнены измерения. Однако дисперсия выражается в единицах в квадрате измеряемой величины. Поэтому в качестве характеристики точности ряда наблюдений наиболее часто применяют среднее квадратическое отклонение (СКО), равное корню квадратному из дисперсии :  .
.
Рассмотренное нормальное распределение случайных величин, в том числе и случайных погрешностей, является теоретическим, поэтому описанное нормальное распределение следует рассматривать как «идеальное», т. е. как теоретическую основу для изучения случайных погрешностей и их влияния на результат измерений.
Далее излагаются способы применения этого распределения на практике с той или иной степенью приближения. Рассматривается также еще одно распределение (распределение Стьюдента), применяемое при небольших количествах наблюдений.
Оценки погрешностей результатов прямых измерений. Пусть было проведено п прямых измерений одной и той же величины. В общем случае в каждом из актов измерений погрешность будет разной:
Di = ai – A,
где Di - погрешность i-го измерения; ai - результат i-го измерения.
Поскольку истинное значение измеряемой величины A неизвестно, непосредственно случайную абсолютную погрешность вычислить нельзя. При практических расчетах приходится вместо A использовать его оценку. Обычно принимают, что истинное значение равно среднему арифметическому значению ряда измерений:
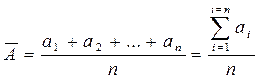 . (4.2)
. (4.2)
где аi - результаты отдельных измерений; п — число измерений.
Теперь аналогично выражению (4.1) можно определить отклонение результата каждого измерения от среднего значения 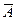 :
:
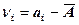 (4.3)
(4.3)
где vi - отклонение результата единичного измерения от среднего значения. Следует помнить, что сумма отклонений результата измерений от среднего значения равна нулю, а сумма их квадратов минимальна, т. е.
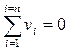 и
и  min.
min.
Эти свойства используются при обработке результатов измерений для контроля правильности вычислений.
Затем вычисляют оценку значения средней квадратической погрешности для данного ряда измерений
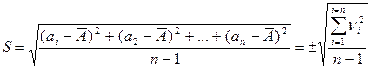 . (4.4)
. (4.4)
Согласно теории вероятностей при достаточно большом числе измерений, имеющих независимые случайные погрешности, оценка S сходится по вероятности к s. Таким образом,
 . (4.5)
. (4.5)
Ввиду того что среднее арифметическое значение 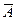 также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения. Эту величину обозначим символом sср. Можно показать, что для независимых погрешностей
также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения. Эту величину обозначим символом sср. Можно показать, что для независимых погрешностей
 . (4.6)
. (4.6)
Значение sср характеризует степень разброса 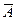 . Как указывалось выше,
. Как указывалось выше, 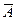 выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому sср называют также средней квадратической погрешностью результата измерений.
выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому sср называют также средней квадратической погрешностью результата измерений.
На практике значением s, вычисляемым по формуле (4.5), пользуются в том случае, если необходимо дать характеристику точности применяемого метода измерения: если метод точен, то разброс результатов отдельных измерений мал, т.е. мало значение s. Значение же sср , вычисляемое по (4.6), используется для характеристики точности результата измерений некоторой величины, т.е. результата, полученного посредством математической обработки итогов целого ряда отдельных прямых измерений.
При оценке результатов измерений иногда пользуются понятием максимальной или предельной допустимой погрешности, значение которой определяют в долях s или S . В настоящее время существуют разные критерии установления максимальной погрешности, т. е. границы поля допуска ±D, в которые случайные погрешности должны уложиться. Общепринятым пока является определение максимальной погрешности D = 3s (или 3S). В последнее время на основании информационной теории измерений профессор П. В. Новицкий рекомендует пользоваться значением D = 2s.
Введем теперь важные понятия доверительной вероятности и доверительного интервала. Как указывалось выше, среднее арифметическое значение 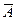 , полученное в результате некоторого ряда измерений, является оценкой истинного значения А и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что
, полученное в результате некоторого ряда измерений, является оценкой истинного значения А и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что 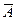 отличается от А не более чем на D, т.е. Р(
отличается от А не более чем на D, т.е. Р(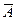 -D< А<
-D< А<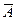 +D)=Рд . Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от
+D)=Рд . Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от 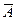 -D до
-D до 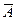 +D - доверительным интервалом.
+D - доверительным интервалом.
Приведенные выше неравенства означают, что с вероятностью Рд доверительный интервал от 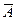 -D до
-D до 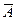 +D заключает в себе истинное значение А. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (п < 20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших п, но значительно отличающуюся от нормальной при малых п.
+D заключает в себе истинное значение А. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (п < 20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших п, но значительно отличающуюся от нормальной при малых п.
В табл. 4.1 приведены так называемые квантили распределения Стьюдента ½t(n)½Рд для числа измерений п = 2 - 20 и доверительных вероятностей Р = 0,5 - 0,999.
Укажем, однако, что обычно таблицы распределения Стьюдента приводятся не для значений п и Рд , а для значений m = n-1 и a =1 – Рд , что следует учитывать при пользовании ими. Чтобы определить доверительный интервал, надо для данных п и Рд найти квантиль ½t(n)½Рд и вычислить величины Ан= 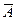 -sср× ½t(n)½РдиАв =
-sср× ½t(n)½РдиАв = 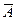 +sср× ½t(n)½Рд, которые будут являться нижней и верхней границами доверительного интервала.
+sср× ½t(n)½Рд, которые будут являться нижней и верхней границами доверительного интервала.
После нахождения доверительных интервалов для заданной доверительной вероятности согласно выше приведенной методике делают запись результата измерения в виде 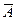 ; D = Dн ¸ Dв ; Рд ,
; D = Dн ¸ Dв ; Рд ,
где 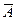 - оценка истинного значения результата измерения в единицах измеряемой величины; D - погрешность измерения; Dв = +sср× ½t(n)½Рд и Dн = -sср× ½t(n)½Рд – верхняя и нижняя границы погрешности измерения; Рд – доверительная вероятность [14].
- оценка истинного значения результата измерения в единицах измеряемой величины; D - погрешность измерения; Dв = +sср× ½t(n)½Рд и Dн = -sср× ½t(n)½Рд – верхняя и нижняя границы погрешности измерения; Рд – доверительная вероятность [14].
– Конец работы –
Эта тема принадлежит разделу:
МЕТРОЛОГИЯ
С В Бирюков А И Чередов... МЕТРОЛОГИЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Вероятностный подход к описанию погрешностей
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов