рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Изобретательство
- /
- Теоретические основы управления в условиях неопределённости
Реферат Курсовая Конспект
Теоретические основы управления в условиях неопределённости
Теоретические основы управления в условиях неопределённости - раздел Изобретательство, - методологические и методические основы подготовки и принятия решений в сложных технико-экономических системах (ТЭС); При Управлении Производством Принимать Решения Очень Часто Приходится Не Имея...
При управлении производством принимать решения очень часто приходится не имея достаточной информации, т.е. в условиях неопределённости и риска.
Методами обоснования решений в условиях неопределённости и риска занимается математическая теория игр.
В теории игр рассматриваются такие ситуации, когда имеются два участника выполнения операции, каждый из которых преследует противоположные цели. В качестве участников могут выступать коллективы, конкурирующие предприятия и т.д. Во всех случаях предполагается, что операция проводится против разумного противника (конкурента), преследующего свои собственные цели и сознательно противодействующего достижению цели другим участником.
Так как цели противоположны, а результат мероприятия каждой из сторон зависит от действий конкурента, то эти действия называют конфликтными ситуациями. В конфликтной ситуации сталкиваются противоположные интересы двух участников. Формализованная (схематизированная) модель конфликтной ситуации называется игрой. Результаты игры – победаили поражение, которые не всегда имеют количественное выражение, можно выразить (условно) числами (например, в шахматах: 1, 0, 1/2).
Игра называется игрой с нулевой суммой, если один из игроков выигрывает ровно столько, сколько проигрывает другой.
Развитие игры по времени представляется как ряд последовательных «ходов». Ходы могут быть сознательные и случайные. Случайный ход – результат, получаемый не решением игрока, а каким-либо механизмом случайного выбора (покупательский спрос, задержка с поставкой материалов и т.п.). Сознательный ход – выбор игроком одного из возможных вариантов действий (стратегии) и принятие решения об его осуществлении.
Возможные варианты (исходы) игры сводятся в прямоугольную таблицу (табл.2.1) – платёжную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы – стратегиям игрока В, qi j называется ценой игры.
Цель теории игр – выработка рекомендаций для различного поведения игроков в конфликтной ситуации, т.е. выбор оптимальной стратегии для каждого из них.
Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строе обозначаются ai и выписываются в виде добавочного столбца матрицы (табл.2.2).
Таблица 2.1
| B1 | B2 | ¼ | Bn | |
| A1 | q11 | q11 | ¼ | q1n |
| A2 | q21 | q22 | ¼ | q2n |
| ¼ | ¼ | ¼ | ¼ | ¼ |
| Am | qm1 | qm2 | ¼ | qmn |
Таблица 2.2
| B1 | B2 | ¼ | Bn | ai | |
| A1 | q11 | q11 | ¼ | q1n | a1 |
| A2 | q21 | q22 | ¼ | q2n | a2 |
| ¼ | ¼ | ¼ | ¼ | ¼ | ¼ |
| Am | qm1 | qm2 | ¼ | qmn | ai |
| bi | b1 | b2 | ¼ | bn |
В каждой строке будет своё 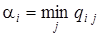 .
.
Предпочтительной для игрока А является стратегия, при которой ai обращается в максимум, т.е.
 или
или  ,
,
где a - максимальный выигрыш (максимин), а соответствующая ей стратегия – максиминная.
Если придерживаться максиминной стратегии, то при любом поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае не меньше a. Поэтому a называют также ценой игры – тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.
Очевидно, что аналогичные распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения выигрыша:
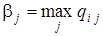 (последняя строка матрицы).
(последняя строка матрицы).
Из всех значений bj находят минимальное:
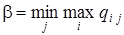 ,
,
которое даёт минимаксный выигрыш или минимакс.
Такая b-стратегия – минимаксная, придерживаясь которой сторона В гарантирована, что в любом случае проиграет не больше b. Поэтому b называют верхней ценой игры.
Если a = b =C, то число С называют чистой ценой игры или седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.
Пример 2.1. Конструктор получил задание разработать определённое новое изделие. В результате исследований он определил три возможных варианта изделия V1, V2, V3, каждый из которых может быть реализован каким-либо из трёх техпроцессов Т1, Т2, Т3.
Если первый вариант конструкции V1 реализуется по первой технологии Т1, то внешний вид изделия оказывается наилучшим и оценивается экспертами в 9 баллов, а при реализации по второй технологии – в 6 баллов, по третьей – в 5 баллов и т.д. (табл.2.3).
Таблица 2.3
| Конструкция | Технология | 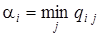
| ||
| Т1 | Т2 | Т3 | ||
| V1 V2 V3 | 7 | 5 (Т3) 7 (Т2 или Т3) 5 (Т2) | ||
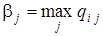
| 7 | 
|
Решение. Конфликтная ситуация возникает из-за того, что затраты на реализацию каждого конструкторско-технологического решения (варианта) не одинаковы. Для простоты полагаем, что затраты пропорциональны внешнему виду (чем выше балл, тем больше затраты).
Конструктор должен представить только один вариант, конечно самый красивый, но он понимает, что тогда найдутся сторонники самого дешёвого варианта («экономисты»). Поэтому его задача выбрать оптимальный вариант по внешнему виду и стоимости.
Если конструктор выберет V1, то экономисты будут настаивать на технологии Т3. На вариант V2 будет ответ Т2 или Т3 и т.д.
Очевидно, что с точки зрения конструктора преимущество имеет вариант V2, а так как даже при неблагоприятных обстоятельствах получиться изделие, оцениваемое в 7 баллов (выигрыш 7), а может быть даже 8, если удаётся уговорить экономистов на вариант Т1.
С точки зрения экономистов в смысле снижения затрат: при выборе технологии Т1 в варианте V1 затраты наибольшие – 9 баллов, при Т2 в V2 (7), при Т3 в V3 (8). То есть для экономистов оптимальным является техпроцесс Т2, так как он требуется меньших затрат при различных вариантах конструкции. Следовательно, стратегия Т2 V2 с выигрышем 7 – наиболее выгодная сразу для обеих сторон – максимальный выигрыш V совпадает с минимальным проигрышем Т.
Однако не все матрицы имеют седловую точку. Тогда решение находят, применяя смешанные стратегии, т.е. чередуя случайным образом несколько чистых стратегий (гибкая тактика).
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называют смешанной стратегией данного игрока.
Из этого определения следует, что сумма компонент этого вектора равна единице, а сами компоненты не отрицательны.
Обычно смешанную стратегию первого игрока обозначают как вектор U= (u1, u2,...,um), а второго игрока – как вектор Z = (z1, z2,...,zm), где ui ³ 0 (i=1...m), zj ³ 0 (j = 1...n),  .
.
Если u0 – оптимальная стратегия первого игрока, z0 – оптимальная стратегия второго игрока, то число 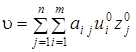 - называют ценой игры.
- называют ценой игры.
Для того, чтобы число u - было ценой игры, а u0 и z0 – оптимальными стратегиями, необходимо и достаточно выполнение неравенств:

Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры u вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии.
Пример 2.2. Найти решение игры, заданной матрицей  .
.
Решение. Прежде всего проверяется наличие седловой точки. Для этого определяются минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5).
Значит, нижняя цена игры
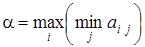 = max(2; 4) = 4,
= max(2; 4) = 4,
верхняя цена игры
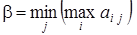 = min(6; 5) = 5.
= min(6; 5) = 5.
Так как a =4 ¹ b = 5, то решение игры – смешанные оптимальные стратегии, а цена игры u в пределах 4 £ u £ 5.
Пусть для игрока А стратегия задаётся вектором U = (u1, u2). Тогда при применении игроком В чистой стратегии В1 или В2 игрок А получить средний выигрыш, равный цене игры, т.е.

Из решения трёх уравнений с тремя неизвестными оптимальная стратегия игрока А:  .
.
Пусть для игрока В стратегия задаётся вектором Z = (z1, z2). Тогда

Отсюда оптимальная стратегия игрока В:  .
.
Следовательно, решением игры будут смешанные стратегии u0=(2/5;3/5), z0 = (1/5; 4/5) с ценой игры u = 22/5.
2.2. Оценка риска в «играх с природой»
В случае, когда между сторонами (участниками) отсутствует «антагонизм» (например, в процессе работы предприятий и торговых посредников), такие ситуации называют «играми с природой».
Здесь первая сторона принимает решение, а вторая сторона – «природа», не оказывает первой стороне сознательного, агрессивного противодействия, но её реальное поведение неизвестно.
Пусть торговое предприятием имеет т стратегий: Т1, Т2,..., Тт и имеется п возможных состояний природы: П1, П2,...,П п. Так как природа не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить выигрышем bi j первой стороны для каждой пары стратегий Тi и Пj. Все показатели игры заданы платёжной матрицей {bi j}mxn.
По платёжной матрице можно принять ряд решений. Например, оценить возможные исходы: минимальный выигрыш
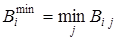 ,
,
т.е. наименьшая из величин в каждой i-1 строке как пессимистическая оценка; максимальный выигрыш – то наилучшее, что даёт выбор i-го варианта
 .
.
При анализе «игры с природой» вводится показатель, по которому оценивают, насколько то или иное состояние «природы» влияет на исход ситуации. Этот показатель называют риском.
Риск ri j при пользовании стратегией Ti и состоянии «природы» Пj оценивается разностью между максимально возможным выигрышем при данном состоянии «природы»  и выигрышем Bi j при выбранной стратегии Тi:
и выигрышем Bi j при выбранной стратегии Тi:
ri j =  – Bi j.
– Bi j.
Исходя из этого определения можно оценить максимальный риск каждого решения:
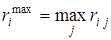 .
.
Решения могут приниматься по результатам анализа ряда критериев.
1. Критерий, основанный на известных вероятностных состояния «природы».
Если известны вероятности состояний «природы» (например, спроса по данным анализа за прошлые годы): Р1 = Р(П1); Р2 = Р(П2);...; Рп = Р(Пп), полагая, что Р1+Р2+...+Рj+...+Рп = 1.
Тогда в качестве показателя эффективности (рациональности, обоснованности) стратегии Тi берётся среднее (математическое ожидание) – выигрыш применения этой стратегии:
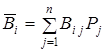 ,
,
а оптимальной считают стратегию, для которой этот показатель эффективности имеет максимальное значение, т.е.
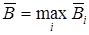 .
.
Если каждому решению Тi соответствует множество возможных результатов Bi j с вероятностями Рi j, то среднее значение выигрыша определится
 ,
,
а оптимальная стратегия выбирается по условию
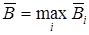 .
.
В этом случае можно воспользоваться и стратегией минимального среднего риска для каждого i-го состояния «природы»
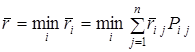 .
.
2. Максиминный критерий Вальда.
Здесь выбирается решение торговой организации, при котором гарантируется максимальный выигрыш в наихудших условиях внешней среды (состояния «природы»):
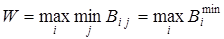 .
.
– Конец работы –
Эта тема принадлежит разделу:
- методологические и методические основы подготовки и принятия решений в сложных технико-экономических системах (ТЭС);
На сайте allrefs.net читайте: - методологические и методические основы подготовки и принятия решений в сложных технико-экономических системах (ТЭС);...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теоретические основы управления в условиях неопределённости
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов