Моделирование экономических процессов в виде системы массового обслуживания

В системах массового обслуживания различают три основных эта­па, которые проходит каждая заявка:

1) появление заявки на входе в систему;

2) прохождение очереди;

3) процесс обслуживания, после которого заявка покидает систему.

На каждом этапе используются определенные характеристики, которые следует обсудить прежде, чем строить математические модели.

Характеристики входа:

1) число заявок на входе (размер популяции);

2) режим поступления заявок в систему обслуживания;

3) поведение клиентов.

Число заявок на входе. Число потенциально возможных заявок (размер популяции) может считаться либо бесконечным (неогра­ниченная популяция), либо конечным (ограниченная популяция). Если число заявок, поступивших на вход системы с момента на­чала процесса обслуживания до любого заданного момента вре­мени, является лишь малой частью потенциально возможного числа клиентов, популяция на входе рассматривается как неогра­ниченная. Примеры неограниченных популяций: автомобили, проходящие через пропускные пункты на скоростных дорогах, покупатели в супермаркете и т.п. В большинстве моделей очередей на входе рассматриваются именно неограниченные популяции.

Если количество заявок, которые могут поступить в систему, сравнимо с числом заявок, уже находящихся в системе массо­вого обслуживания, популяция считается ограниченной. Пример ограниченной популяции: компьютеры, принадлежащие конкрет­ной организации и поступающие на обслуживание в ремонтную мастерскую.

Режим поступления заявок, в систему обслуживания. Заявки могут поступать в систему обслуживания в соответствии с опреде­ленным графиком (например, один пациент на прием к стомато­логу каждые 15 мин, один автомобиль на конвейере каждые 20 мин) или случайным образом. Появления клиентов считаются случай­ными, если они независимы друг от друга и точно непредсказу­емы. Часто в задачах массового обслуживания число появлений в единицу времени может быть оценено с помощью пуассоновского распределения вероятностей. При заданном темпе поступления (например, два клиента в час или четыре грузовика в минуту) дискретное распределение Пуассона описывается следующей фор­мулой:

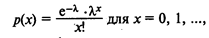
где р (х) — вероятность поступления х заявок в единицу вре­мени;

х — число заявок в единицу времени;

l — среднее число заявок в единицу времени (темп по­ступления заявок);

е = 2,7182 — основание натурального логарифма.

Соответствующие значения вероятностей р(х) нетрудно опре­делить с помощью таблицы пуассоновского распределения. Если, например, средний темп поступления заявок — два клиента в час, то вероятность того, что в течение часа в систему не поступит ни одной заявки, равна 0,135, вероятность появления одной заявки — около 0,27, двух — также около 0,27, три заявки могут появиться с вероятностью 0,18, четыре — с вероятностью около 0,09 и т.д. Вероятность того, что за час в систему поступят 9 заявок или бо­лее, близка нулю.

На практике вероятности появления заявок, разумеется, не всегда подчиняются пуассоновскому распределению (они могут иметь какое-то другое распределение). Поэтому требуется прово­дить предварительные исследования для того, чтобы проверить, что пуассоновское распределение может служить хорошей аппрок­симацией.

Поведение клиентов. Большинство моделей очередей основы­вается на предположении, что поведение клиентов является стан­дартным, т.е. каждая поступающая в систему заявка встает в оче­редь, дожидается обслуживания и не покидает систему до тех пор, пока ее не обслужат. Другими словами, клиент (человек или ма­шина), вставший в очередь, ждет до тех пор, пока он не будет обслужен, не покидает очередь и не переходит из одной очереди в другую.

Жизнь значительно сложнее. На практике клиенты могут по­кинуть очередь потому, что она оказалась слишком длинной. Может возникнуть и другая ситуация: клиенты дожидаются сво­ей очереди, но по каким-то причинам уходят необслуженными. Эти случаи также являются предметом теории массового обслу­живания, однако здесь не рассматриваются.

Характеристики очереди:

1) длина;

2) правило обслуживания.

Длина очереди. Длина может быть ограничена либо не ограни­чена. Длина очереди (очередь) ограничена, если она по каким-либо причинам (например, из-за физических ограничений) не может увеличиваться до бесконечности. Если очередь достигает своего максимального размера, то следующая заявка в систему не допускается и происходит отказ. Длина очереди не ограничена, если в очереди может находиться любое число заявок. Например, очередь автомобилей на бензозаправке.

Правило обслуживания. Большинство реальных систем исполь­зует правило «первым пришел — первым ушел» (FIFO — first in, first out). В некоторых случаях, например в приемном покое боль­ницы, в дополнение к этому правилу могут устанавливаться раз­личные приоритеты. Пациент с инфарктом в критическом со­стоянии, по-видимому, будет иметь приоритет в обслуживании по сравнению с пациентом, сломавшим палец. Порядок запуска компьютерных программ — другой пример установления приорите­тов в обслуживании.

Характеристики процесса обслуживания:

1) конфигурация системы обслуживания (число каналов и чис­ло фаз обслуживания);

2) режим обслуживания.

Конфигурация системы обслуживания. Системы обслуживания различаются по числу каналов обслуживания. Обычно количество каналов можно определить как число клиентов, обслуживание которых может быть начато одновременно, например: число мас­теров в парикмахерской. Примеры одноканальной системы об­служивания: банк, в котором открыто единственное окошко для обслуживания клиентов, или ресторан, обслуживающий клиентов в автомобилях. Если же в банке открыто несколько окошек для обслуживания, клиент ожидает в общей очереди и подходит к пер­вому освободившемуся окну, то мы имеем дело с многоканаль­ной однофазовой системой обслуживания. Большинство банков, также, как почтовые отделения и авиакассы, являются многока­нальными системами обслуживания.

Другая характеристика — число фаз (или последовательных этапов) обслуживания одного клиента. Однофазовыми являют­ся такие системы, в которых клиент обслуживается в одном пун­кте (на одном рабочем месте), затем покидает систему. Ресторан для обслуживания автомобилей, в котором официант получает деньги и приносит заказ в автомобиль, является примером од­нофазовой системы. Если же в ресторане нужно сделать заказ в одном месте, оплатить его в другом и получить пищу в третьем, то мы имеем дело с многофазовой (три фазы) системой обслу­живания.

На рис. 1 приведены системы обслуживания различной кон­фигурации.

Рис. 1

Режим обслуживания. Как и режим поступления заявок, режим обслуживания может характеризоваться либо постоянным, либо случайным временем обслуживания. При постоянном времени на обслуживание любого клиента затрачивается одинаковое вре­мя. Такая ситуация может наблюдаться на автоматической мойке автомобилей. Однако более часто встречаются ситуации, когда время обслуживания имеет случайное распределение. Во многих случаях можно предположить, что время обслуживания подчиня­ется экспоненциальному распределению с функцией распреде­ления

F(t) = p(t< t) =1 – е^–tm, где р (t < t) — вероятность того, что фактическое время t обслу­живания заявки не превысит заданной величи­ны t;

m — среднее число заявок, обслуживаемых в едини­цу времени;

е = 2,7182 — основание натурального логарифма.

Параметры моделей очередей. При анализе систем массового обслуживания используются технические и экономические харак­теристики.

Наиболее часто используются следующиетехнические характери­стики:

1) среднее время, которое клиент проводит в очереди;

2) средняя длина очереди;

3) среднее время, которое клиент проводит в системе обслужи­вания (время ожидания плюс время обслуживания);

4) среднее число клиентов в системе обслуживания;

5) вероятность того, что система обслуживания окажется незанятой;

6) вероятность определенного числа клиентов в системе.

Средиэкономических характеристик наибольший интерес пред­ставляют следующие:

1) издержки ожидания в очереди;

2) издержки ожидания в системе;

3) издержки обслуживания.

Модели систем массового обслуживания. В зависимости от со­четания приведенных выше характеристик могут рассматривать­ся различные модели систем массового обслуживания.

Здесь мы ознакомимся с несколькими наиболее известными моделями. Все они имеют следующие общие характеристики:

а) пуассоновское распределение вероятностей поступления заявок;

б) стандартное поведение клиентов;

в) правило обслуживания FIFO (первым пришел — первым об­служен);

г) единственная фаза обслуживания.

I. Модель А — модель одноканальной системы массового об­служивания М/М/1 с пуассоновским входным потоком заявок и экспоненциальным временем обслуживания.

Наиболее часто встречаются задачи массового обслуживания с единственным каналом. В этом случае клиенты формируют одну очередь к единственному пункту обслуживания. Предположим, что для систем этого типа выполняются следующие условия:

1. Заявки обслуживаются по принципу «первым пришел — пер­вым обслужен» (FIFO), причем каждый клиент ожидает своей очереди до конца независимо от длины очереди.

2. Появления заявок являются независимыми событиями, од­нако среднее число заявок, поступающих в единицу времени, не­изменно.

3. Процесс поступления заявок описывается пуассоновским распределением, причем заявки поступают из неограниченного множества.

4. Время обслуживания описывается экспоненциальным рас­пределением вероятностей.

5. Темп обслуживания выше темпа поступления заявок.

Пусть l — число заявок в единицу времени;

m — число клиентов, обслуживаемых в единицу времени;

п — число заявок в системе.

Тогда система массового обслуживания описывается уравнени­ями, приведенными ниже.

Формулы для описания системы М/М/1:

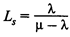— среднее число клиентов в системе;

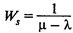— среднее время обслуживания одного клиента в системе (время ожидания плюс время обслуживания);

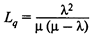— среднее число клиентов в очереди;

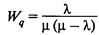— среднее время ожидания клиента в очереди;

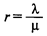— характеристика загруженности системы (доля време­ни, в течение которого система занята обслуживанием);

— вероятность отсутствия заявок в системе;

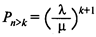— вероятность того, что в системе находится бо­лее чем k заявок.

II. Модель В — многоканальная система обслуживания M/M/S. В многоканальной системе для обслуживания открыты два ка­нала или более. Предполагается, что клиенты ожидают в общей очереди и обращаются в первый освободившийся канал обслужи­вания.

Пример такой многоканальной однофазовой системы можно увидеть во многих банках: из общей очереди клиенты обращают­ся в первое освободившееся окошко для обслуживания.

В многоканальной системе поток заявок подчиняется пуассоновскому закону, а время обслуживания — экспоненциальному. Приходящий первым обслуживается первым, и все каналы обслу­живания работают в одинаковом темпе. Формулы, описывающие модель В, достаточно сложны для использования. Для расчета параметров многоканальной системы обслуживания удобно ис­пользовать соответствующее программное обеспечение.

Для многоканальной системы с неограниченной очередью должно выполняться условие < 1, где r — параметр загрузки системы (среднее число занятых каналов), п — минимальное ко­личество каналов, при котором очередь не будет расти до беско­нечности. В противном случае предельные вероятности существо­вать не могут.

Формулы для описания системы M/M/S:

— вероятность того, что система свободна;

— вероятность того, что в системе находится п заявок;

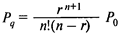— вероятность того, что заявка окажется в очереди;

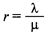— среднее число занятых каналов;

— среднее число заявок в очереди;

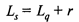— среднее число заявок в системе;

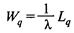— время нахождения заявки в очереди;

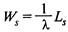— время нахождения заявки в системе.

III. Модель С— модель с постоянным временем обслуживания M/D/1.

Некоторые системы имеют постоянное, а не экспоненциально распределенное время обслуживания. В таких системах клиенты обслуживаются в течение фиксированного периода времени, как, например, на автоматической мойке автомобилей. Для модели С с постоянным темпом обслуживания значения величин L_q и W_q вдвое меньше, чем соответствующие значения в модели А, име­ющей переменный темп обслуживания.

Формулы, описывающие модель С:

— средняя длина очереди;

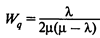— среднее время ожидания в очереди;

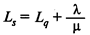— среднее число клиентов в системе;

— среднее время ожидания в системе.

IV. Модель D — модель с ограниченной популяцией.

Если число потенциальных клиентов системы обслуживания ограничено, мы имеем дело со специальной моделью. Такая за­дача может возникнуть, например, если речь идет об обслужива­нии оборудования фабрики, имеющей пять станков.

Особенность этой модели по сравнению с тремя рассмотрен­ными ранее в том, что существует взаимозависимость между длиной очереди и темпом поступления заявок.

V. Модель Е — модель с ограниченной очередью. Модель от­личается от предыдущих тем, что число мест в очереди ограни­чено. В этом случае заявка, прибывшая в систему, когда все ка­налы и места в очереди заняты, покидает систему необслуженной, т.е. получает отказ.

Как частный случай модели с ограниченной очередью можно рассматривать модель с отказами, если количество мест в очере­ди сократить до нуля.

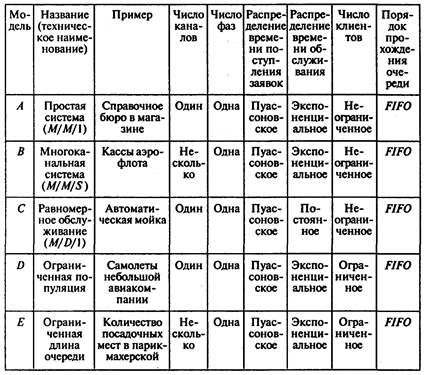
Сравнительная характеристика различных моделей систем массового обслуживания приведена в следующей таблице: