Общее понятие имитационного моделирования экономических процессов

Общее понятие имитационного моделирования экономических процессов.

Имитационное моделирование на цифровых вычислительных машинах является одним из наиболее мощных средств исследования, в частности, сложных… В настоящее время, когда компьютерная промышленность, предлагает…

Пакеты визуального моделирования

Одним из главных достоинств систем визуального моделирования является то, что они позволяют пользователю не заботится о программной реализации… Программная реализация виртуального стенда скрыта от пользователя. Для… Еще одной важной особенностью современного пакета автоматизации моделирования является использование технологии…

Объектно-ориентированное моделирование

Основные понятия

Объектно-ориентированное моделирование (ООМ) предполагает поддержку классов и экземпляров блоков, а также наследования и полиморфизма блоков.

Класс определяет некоторый шаблон или прототип блока (например, бассейн вообще). Оперируя с классом, например "Бассейн", нельзя говорить о конкретном значении уровня воды в нем, так как в определении класса присутствуют только информация о типах и именах используемых переменных, но не об их значениях.

Экземпляр блока - это конкретный представитель класса блоков, например, Бассейн_1 и Бассейн_2. Каждый экземпляр имеет свои собственные значения переменных (уровни воды в двух бассейнах могут быть разными). При создании нового экземпляра могут быть конкретизированы его параметры - специальные константы, которые не могут быть, как и любые константы, изменены в процессе функционирования, но могут оказаться разными для различных экземпляров. В функциональную схему могут входить несколько экземпляров одного и того же класса, например, выходная труба блока Бассейн_1 может являться входной для блока Бассейн_2.

Экземпляры могут быть статическими и динамическими. Статический экземпляр создается при создании модели и уничтожается при ее уничтожении. Например, каскад бассейнов явно является статической структурой. Динамические экземпляры создаются и уничтожаются в ходе моделирования. Например, при моделировании работы системы ПВО число самолетов в зоне видимости радиолокатора переменно.

Вообще говоря, понятия класса и экземпляра поддерживались явно или неявно практически всеми языками моделирования. В противном случае достаточно сложно моделировать системы с множеством однотипных блоков и невозможно моделировать системы с динамической структурой.

Более сложными понятиями ООМ являются наследование и полиморфизм.

Часто возникает необходимость создать новый класс "такой же, но ...". Например, нужно описать бассейн с подогревом воды, дополнив описание стандартного бассейна нужными деталями. В этом новом классе "Бассейн_с_подогревом" описание интерфейса и динамики уровня воды будет точно таким же, как и в классе "Бассейн". К нему добавится свое описание тепловых потоков и динамики температуры.

Можно просто перенести в описание нового класса элементы описания старого и добавить новые. Но можно объявить новый класс прямым потомком старого. В этом случае класс "Бассейн" будет являться суперклассом (родителем, базовым классом) для класса "Бассейн_с_подогревом", а тот в свою очередь будет являться подклассом (потомком, производным классом) по отношению к классу "Бассейн". В этом случае производный класс автоматически унаследует все элементы описания своего базового класса. Следует отметить, что наследование не означает простого копирования. Между классами возникает постоянная связь: если в классе "Бассейн" добавить новую переменную состояния (например, показатель хлорированности воды), то она автоматически появится в классе "Бассейн_с_подогревом".

Полиморфизм означает возможность использования вместо экземпляра блока некоторого базового класса экземпляра любого его производного класса. Например, для радиолокационной станции все сопровождаемые объекты являются экземплярами класса "Летательный_аппарат" и характеризуются только положением и вектором скорости. На самом же деле эти объекты могут являться самыми разнообразными потомками класса "Летательный_аппарат" от B-52 до птеродактиля.

Библиотеки классов

Наличие богатых библиотек классов является серьезным преимуществом той или иной системы моделирования. В этом случае модель может строиться механически из экземпляров стандартных классов с их параметрической настройкой. Возможности среды увеличиваются, если библиотеки классов создаются самим прикладным пользователем.

Следует отметить, что при построении библиотеки классов чрезвычайно удобным оказывается использование неориентированных блоков, поскольку это дает возможность создавать блоки, максимально независимые от внешнего окружения.

Численное решение

Максимально удобным для численного решения является явное представление моделируемой системы в виде такой гибридной, в которой все скачкообразные… Таким образом, задача численного нахождения решения распадается на… 1) выявление скрытой гибридности в описании непрерывных систем и построение гибридной системы, где узлам приписаны…

Существующие подходы к визуальному моделированию сложных динамических систем

Их можно условно разделить на три группы: 1) пакеты "блочного моделирования": 2) пакеты "физического моделирования":

Классификация моделей.

• Математические модели.

В основе их построения лежит допущение о том, что все релевантные(переставляемые) переменные, параметры и ограничения, а также целевая функция количественно измеримы. Поэтому, если x_j, j=1,2,...,n представляют собой n управляемых переменных и условия функционирования исследуемой экономической системы характеризуются m ограничениями, то математическая модель может быть записана в следующем виде:

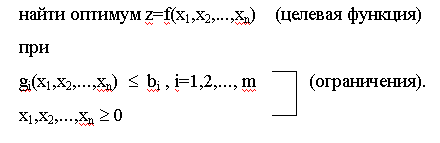
Ограничения x₁,x₂,...,x_n >= 0 называются условиями неотрицательности. Эти условия требуют, чтобы переменные принимали только положительное или нулевое значение. В большинстве практических случаев такое требование вполне естественно. Нахождение оптимума осуществляется для определения наилучшего значения целевой функции, например, максимума прибыли или минимума затрат.

Общие классы математических моделей: модели линейного, целочисленного и динамического программирования, вероятностные модели, модели нелинейного программирования.

• Имитационные модели.

Воспроизводят поведение системы на протяжении некоторого промежутка времени. Это достигается путем идентификации ряда событий, распределение которых во времени дает важную информацию о поведении системы. После того как такие события определены, требуемые характеристики системы необходимо регистрировать только в моменты реализации этих событий. Информация характеристиках системы накапливается в виде статистических данных таких наблюдений. Эта информация обновляется всякий раз при наступлении каждого из интересующих нас событий.

Для построения имитационных моделей не требуется использования математических функций, явным образом связывающих те или иные переменные. Эти модели позволяют имитировать поведение сложных систем, для которых построение математических моделей и получение решений невозможно. Более того, гибкость, присущая имитационным моделям, позволяет добиться более точного представления системы.

Основной недостаток имитационного моделирования заключается в том, что его реализация эквивалентна проведению множества экспериментов, а это неизбежно обусловливает наличие экспериментальных ошибок. Кроме того, сам процесс оптимизации также вызывает затруднения.

• Эвристические методы.

Базируются на интуитивно или эмпирически выбираемых правилах, которые позволяют улучшить уже имеющееся решение. Используются в том случае, когда соответствующие математические построения оказываются настолько сложными, точное решение сформулированной задачи найти нельзя.

По, существу эвристические методы представляют собой процедуры поиска разумного перехода от одной точки пространства решений к некоторой другой точке с целью улучшения текущего значения целевой функции модели. Когда дальнейшего приближения к оптимуму добиться невозможно, лучшее из полученных решений принимается в качестве приближенного решения оптимизационной задачи.

Оптимизация заданной целевой функции.

Основной вывод, который следует из вышеизложенного, заключается в том, что полученное с помощью некоторой модели конкретное оптимальное решение…

Проблема информационного обеспечения моделей.

Любая модель экономической системы независимо от ее сложности и адекватности системе-оригиналу принесет мало пользы при отсутствии необходимой информации.

Предположим, например, что некоторое предприятие выпускает продукцию двух видов, изготавливаемую из одного и того же сырья, имеющегося в ограниченном количестве. Пусть расход сырья на изготовление единицы продукции вида 1 равен а₁, а продукции вида 2 - а₂. Если через b обозначить имеющийся запас сырья, то при объемах производства каждого вида продукции, равных х₁ и х₂ соответственно, рассматриваемый производственный процесс характеризуется ограничением а₁ х_{1 +} а₂ х₂ <= b . Приступая к решению такой задачи мы должны найти значения а₁, а₂, и b. Определение этих параметров может оказаться затруднительным и потребовать тщательного анализа большого объема данных, характеризующих работу всего предприятия.

Этапы исследования экономических процессов.

1) идентификации проблемы; 2) построения модели; 3) решения поставленной задачи с помощью модели;

Сетевая модель.

Для представления операции используется стрелка, направление которой соответствует процессу реализации программы во времени. Отношение упорядочения между операциями задается с помощью событий. Событие… Начальная и конечная точка любой операции описываются, таким образом, парой событий, которые обычно называют начальным…

Правила построения сетевой модели.

Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда… Правило 2. Ни одна пара операций не должна определяться одинаковыми начальными… Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число…

Моделирование экономических процессов в виде системы массового обслуживания

1) появление заявки на входе в систему; 2) прохождение очереди; 3) процесс обслуживания, после которого заявка покидает систему.

Примеры

Пример 1. Обслуживание автомобилей.

Иванов, механик автосервиса, может заменить масло в сред­нем в трех автомобилях в течение часа (т.е. в среднем на одном автомобиле за 20 мин). Время обслуживания подчиняется экспо­ненциальному закону. Клиенты, нуждающиеся в этой услуге, при­езжают в среднем по два в час, в соответствии с пуассоновским распределением. Клиенты обслуживаются в порядке прибытия, и их число не ограничено. Рассчитайте основные характеристики системы обслуживания.

Решение. На основе исходных данных получаем:

l = 2 машины в час — количество машин, поступающих в те­чение часа;

m = 3 машины в час — количество машин, обслуживаемых в течение часа;

машины — среднее количество машин, находящихся в системе;

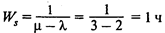— среднее время ожидания в системе;

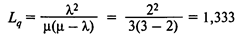машины — среднее коли­чество машин, ожидающих в очереди;

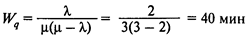— среднее время ожи­дания в очереди;

— доля времени, в течение которого меха­ник занят;

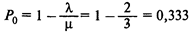— вероятность того, что в систе­ме нет ни одного клиента.

Вероятности того, что в системе находится более чем k машин:

Примечание. При k = 0 значение вероятности равно 1 – P₀;

при k = 1 существует 44,4% шансов на то, что в системе находит­ся более одной машины, и т.д.

Пример 2. Сопоставление затрат.

После того как мы получили основные характеристики систе­мы обслуживания, часто бывает полезным провести ее экономи­ческий анализ. Как уже отмечалось, задачей менеджера является сопоставление возрастающих затрат на улучшение обслуживания и снижающихся затрат, связанных с ожиданием. Рассмотрим этот случай, дополнив условие примера 1.

Владелец автосервиса установил, что затраты, связанные с ожи­данием, выражаются в снижении спроса вследствие неудовлетво­ренности клиентов и равны 100 руб. за час ожидания в очереди. Определите общие затраты функционирования автосервиса.

Решение. Так как в среднем каждая машина ожидает в очере­ди 2/3 часа (W_q) и в день обслуживается приблизительно 16 ма­шин (l×8 = 2 машины в час в течение 8-часового рабочего дня), общее число часов, которое проводят в очереди все клиенты, равно

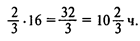
Следовательно, затраты, связанные с ожиданием, составляют

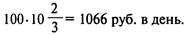
Другая важная составляющая затрат владельца автосервиса — зарплата механика Иванова. Предположим, что он получает 70 руб. в час, или 560 руб. в день. Следовательно, общие затраты состав­ляют

1066 + 560 = 1626 руб. вдень.

Пример 3. Утилизация отходов.

Компания «Утиль» собирает и утилизирует в Мытищах алюми­ниевые отходы и стеклянные бутылки. Водители автомобилей, доставляющих сырье для вторичной переработки, ожидают в оче­реди на разгрузку в среднем 15 мин. Время простоя водителя и автомобиля оценивается в 6 тыс. руб. в час.

Новый автоматический компактор может обслуживать контейнеровозы с постоянным темпом 12 машин в час (5 мин на одну машину). Время прибытия контейнеровозов подчиняется пуассоновскому закону с параметром l = 8 автомобилей в час. Если но­вый компактор будет использоваться, то амортизационные затра­ты составят 0,3 тыс. руб. на один контейнеровоз. Следует ли ис­пользовать компактор?

Решение. Затраты на простой одного автомобиля в очереди за одну ездку в системе без компактора составляют

В системе с компактором время ожидания в очереди при l = 8 автомобилей в час и m = 12 автомобилей в час будет равно

Затраты на простой автомобиля в очереди в этом случае составят

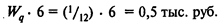
Сокращение времени простоя привело к сокращению затрат на простой одного автомобиля за одну ездку на сумму в 1,5 – 0,5 = 1 тыс. руб.

При условии, что затраты по эксплуатации компактора на один контейнеровоз составляют 0,3 тыс. руб., общие затраты составят 0,5 + 0,3 = 0,8 тыс. руб.

Система с компактором дает экономию в 1,5 – 0,8 = 0,7 тыс. руб. Таким образом, компактор использовать следует.

Имитационное моделирование управления запасами

1) его доля в общем количестве запасов фирмы; 2) его доля в общей стоимости запасов. Методика 20/80.В соответствии с этой методикой компонен­ты запаса, составляющие 20% его общего количества и 80% его…

I. Детерминированные модели

Простейшая модель оптимального размера заказа.

1) темп спроса на товар известен и постоянен; 2) получение заказа мгновенно; 3) закупочная цена не зависит от размера заказа;

Модель оптимального размера заказа с фиксированным вре­менем его выполнения.

1) темп спроса на товар известен и постоянен; 2) время выполнения заказа известно и постоянно; 3) закупочная цена не зависит от размера заказа;

Модель оптимального размера заказа с производством.

1) темп спроса на товар известен и постоянен; 2) темп производства товара известен и постоянен; 3) время выполнения заказа известно и постоянно;

Модель оптимального размера заказа с дефицитом.

1) темп спроса на товар известен и постоянен; 2) время выполнения заказа известно и постоянно; 3) закупочная цена не зависит от размера заказа.

Модель оптимального размера заказа с количественными скидками.

1) темп спроса на товар известен и постоянен; 2) время выполнения заказа известно и постоянно. Исходные данные: темп спроса, издержки заказа, издержки хра­нения, цена товара, количественные скидки в случае закупки…

II. Стохастическая модель

Дискретная стохастическая модель оптимизации начально­го запаса.

Пусть S — размер запаса на начало периода планирования; D — величина спроса за период планирования (це­лое число); Н — удельные издержки хранения за период;

Примеры

Пример 1. Продажа автомобилей.

Андрей Удачливый, торговый агент компании Volvo, занима­ется продажей последней модели этой марки автомобиля. Годо­вой спрос на эту модель оценивается в 4000 единиц. Цена каждо­го автомобиля равна 90 тыс. руб., а годовые издержки хранения составляют 10% от цены самого автомобиля. Анализ показал, что средние издержки заказа составляют 25 тыс. руб. на заказ. Время выполнения заказа — 8 дней. Ежедневный спрос на автомобили равен 20.

Вопросы:

1. Чему равен оптимальный размер заказа?

2. Чему равна точка восстановления?

3. Каковы совокупные издержки?

4. Каково оптимальное количество заказов в год?

5. Каково оптимальное время между двумя заказами, если предположить, что количество рабочих дней в году равно 200?

Решение. Исходные данные:

величина спроса D = 4000 единиц;

издержки заказа K = 25 тыс. руб.;

издержки хранения H = 9/200 тыс. руб.;

цена за единицу с = 90 тыс. руб.;

время выполнения заказа L = 8 дней;

ежедневный спрос d = 20 единиц;

число рабочих дней Т= 200.

Используя простейшую модель оптимального размера заказа, получаем:

размер заказа Q = 149 единиц;

точка восстановления R = 160 единиц;

число заказов за год N= 26,83;

совокупные издержки С = 1341 тыс. руб;

стоимость продаж cD = 360 млн руб.;

число дней между заказами t = 7,45.

Пример 2. Поставка товара с фиксированным интервалом времени.

Магазин «Лада» закупает духи «Ландыш» на одной из парфю­мерных фабрик. Годовой спрос на этот продукт составляет 600 шт. Издержки заказа равны 850 руб., издержки хранения — 510 руб за одну упаковку (20 шт.) в год. Магазин заключил договор на поставку с фиксированным интервалом времени.

Количество рабочих дней в году — 300. Время поставки товара — б дней. Стоимость одного флакона — 135 руб.

Вопросы:

1. Чему равно оптимальное число заказов в течение года?

2. Чему равна точка восстановления запаса?

3. Каковы минимальные совокупные издержки?

Решение. Оптимальный размер заказа

Число заказов в течение года

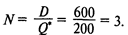
Поскольку среднесуточный спрос равен 600/300 = 2 шт., точ­ка восстановления запаса составит 2 • 6 = 12 шт. Минимальные издержки заказа и хранения

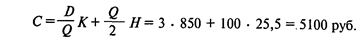
Ответы: 1.3. 2.12шт. 3.5100руб.

Пример 3. Производство деталей.

На первом станке производятся детали в количестве 12 000 еди­ниц в год. Эти детали используются для производства продукции на втором станке производительностью 3600 единиц в год. Остав­шиеся детали образуют запас. Издержки хранения составляют 0,5 руб. за одну деталь в год. Стоимость производственного цикла на первом станке равна 800 руб. Определите оптимальный размер партии на первом станке.

Решение. Оптимальный размер партии

Пример 4. Планирование дефицита.

Вернемся к примеру 2 и рассмотрим вариант планирования дефицита. Допустим, по оценке менеджера, упущенная прибыль, связанная с отсутствием товара и утратой доверия клиентов, со­ставляет 20 руб. в год за один флакон духов «Ландыш» при усло­вии, что издержки заказа и хранения остаются без изменения. Определите оптимальный размер заказа при плановом дефиците. Нужно ли менеджеру вводить систему с плановым дефицитом?

Решение. Оптимальный размер заказа

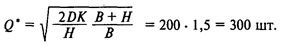
Максимальный размер запаса за один цикл

Совокупные издержки

Совокупные издержки при плановом дефиците меньше издер­жек без дефицита на 1718,7 руб. Следовательно, целесообразно ввести систему с плановым дефицитом.

Пример 5. Продажи со скидками.

Магазин «Медвежонок» продает игрушечные гоночные машин­ки. В зависимости от размера заказа фирма предлагает скидки:

Издержки заказа составляют 49 руб. Годовой спрос на машин­ки равен 5000. Годовые издержки хранения в процентном отно­шении к цене составляют 20%. Найдите размер заказа, миними­зирующий общие издержки.

Решение. Рассчитаем Q* для каждого вида скидок: Q₁* = 700, Q₂* = 714, Q₃* =718.

Так как Q₁* находится в интервале между 0 и 1000, то его необ­ходимо взять равным 700. Оптимальный объем со скидкой Q₂* меньше количества, необходимого для получения скидки, следо­вательно, его необходимо принять равным 1000 единиц. Анало­гично Q₃* берем равным 2000 единиц.

Получим: Q₁* = 700, Q₂* = 1000, Q₃* = 2000.

Далее необходимо рассчитать общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значе­ние. Расчеты приведены в следующей таблице:

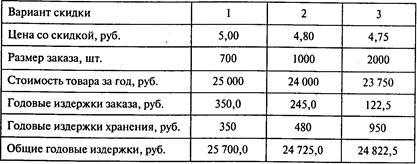
Выберем тот размер заказа, который минимизирует общие го­довые издержки. Из таблицы видно, что заказ в размере 1000 игру­шечных машинок будет минимизировать совокупные издержки.

Пример 6. Создание запаса продукции при дискретном спросе. Небольшой салон специализируется на продаже видеомагни­тофонов стоимостью 2000 руб. Затраты на хранение единицы про­дукции составляют 500 руб. Изучение спроса, проведенное в те­чение месяца, дало следующее распределение числа покупаемых видеомагнитофонов:

Найдите оптимальный размер запаса.

Решение. Доказано, что при дискретном случайном спросе сум­марные затраты C(S) = Н 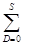(S–D)p(D) + В (D–S)p(D) минимальны при размере запаса S*, удовлетворяющем неравенству 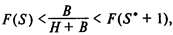где — плотность убытков, F(S)=р(D<S) — функция распределения величины спроса. Вычислим плотность убытков:

Найдем значения функции распределения величины спроса:

Оптимальный размер запаса продукции удовлетворяет неравен­ству F(6) < 0,8 < F(7). Следовательно, размер запаса в 6 единиц будет оптимальным.

Основы теории матричных игр

а) заинтересованных сторон; б) возможных действий каждой из сторон; в) интересов сторон.

Матричная игра двух лиц с нулевой суммой

Игра, в которой множества А и В стратегий игроков конечны, т.е. |А| < ¥, |В| < ¥, называется матричной. В этом случае функ­ция… Элементы матрицы могут быть положительными, отрицатель­ными или равными нулю.… Игрок 1 стремится к максимальному выигрышу, игрок 2 — к минимальному проигрышу. Решить игру — значит найти…

Матричная игра двух лиц с ненулевой постоянной суммой

Такого рода игра сводится к игре двух лиц с нулевой суммой следующим образом: 1) каждому игроку выплачивается сумма с/2; 2) решается игра с нулевой суммой с матрицей выигрышей игрока 1, где

Примеры

Пример 1. Выбор стратегии. Матрица некоторой игры имеет вид

Найдите оптимальные стратегии игроков.

Решение. В этой игре игрок 1 имеет три возможные страте­гии: а₁, а₂, а₃ из, а игрок 2 — четыре возможные стратегии: b₁, b₂, b₃, b₄.

Рассмотрим процесс принятия игроками решения (предпола­гается, что они действуют рационально). Взглянув на таблицу, можно заметить, что если игрок 1 не знает, как поступит его про­тивник, то, действуя наиболее целесообразно и считая, что про­тивник будет действовать подобным же образом, он выберет стра­тегию а₂, которая гарантирует ему наибольший из трех возмож­ных наименьших выигрышей: 9, 13, 8. Другими словами, игрок 1 руководствуется принципом максиминного выигрыша. Этот выигрыш a = 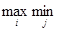а_ij есть нижняя цена игры. Для нашего примера a = 13.

Игрок 2 рассуждает аналогично: если он выберет стратегию b₁, ,то потеряет самое большее 23, если стратегию b₂, то — 40, и т.д. В результате он выберет стратегию b₃, которая гарантирует ему наименьший из четырех возможных проигрышей: 23, 40, 13, 25. Принято говорить, что игрок 2 руководствуется принципом мини­максного проигрыша. Этот проигрыш b = 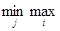а_ij есть верхняя цена игры. Для нашей матрицы b = 13.

Ситуация (a₂, b₃) есть седловая точка, и a = b = 13 есть цена игры.

При наличии седловой точки ни одному из участников игры невыгодно отклоняться от своей минимаксной стратегии: он бу­дет наказан противником тем, что получит меньший выигрыш.

Пример 2. Где строить?

Две конкурирующие крупные торговые фирмы Ф₁ и Ф₂ пла­нируют построить в одном из четырех небольших городов Г₁, Г₂, Г₃ и Г₄, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и чис­ленность населения показаны на рис. 1.

Рис. 1

Прибыль каждой фирмы зависит от численности населения городов и степени удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследова­ние показало, что прибыль в универсамах будет распределяться между фирмами следующим образом:

Например, если универсам фирмы Ф₁ расположен к городу Г₁ ближе универсама фирмы Ф ₂, то прибыль от покупок, сделанных жителями данного города, распределится следующим образом: 75% получит Ф₁, остальное — Ф ₂.

Представьте описанную ситуацию как игру двух лиц.

В каких городах фирмам целесообразно построить свои уни­версамы?

Решение. Составим платежную матрицу игры, в которой иг­роком 1 будет фирма Ф ₁, а игроком 2 — фирма Ф₂. Стратегии обо­их игроков: строить свой универсам в городе Г₁, в городе Г₂ и т.д. Элементы матрицы — прибыль фирмы Ф₁ (в тыс. руб.), которая, как предполагается, пропорциональна (причем с одним и тем же коэффициентом) числу покупателей. Величина указанного коэф­фициента пропорциональности для выбора оптимального места размещения универсамов значения не имеет, поэтому примем его равным единице.

Платежная матрица имеет вид

Рассмотрим примеры расчета значений элементов (Г₁, Г₂) и (Г₃, Г₄) матрицы.

Ситуация (Г₁, Г₂) означает, что фирма Ф₁, строит универсам в городе Г₁, а фирма Ф₂ — в городе Г₂. Число покупателей фирмы Ф₁ складывается из покупателей четырех городов. Для ситуации (Г₁, Г₂) число покупателей из Г₁: 0,75×30, из Г₂: 0,45×50, из Г₃ 0,45×40, из Г₄: 0,45×30, т.е. в сумме 76,5 тыс. руб. Для ситуации (Г₃, Г₄) число покупателей из Г₁: 0,75×30, из Г₂: 0,75×50, из Г₃: 0,75×40, из Г₄: 0,45×30, т.е. в сумме 103,5 тыс. руб. Элементы мат­рицы выигрышей фирмы Ф₂ — дополнения до числа 150 (общее число жителей в четырех городах). Таким образом, имеет место игра двух лиц с ненулевой постоянной суммой, оптимальные стратегии которой те же, что и для соответствующей игры с ну­левой суммой.

Полученная платежная матрица имеет седловую точку (Г₂, Г₂). Соответствующий элемент матрицы равен 90.

Таким образом, обеим фирмам следует строить свои универ­самы в одном и том же городе Г₂, при этом прибыль фирмы Ф₁ составит 90 тыс., а фирмы Ф₂ — 60 тыс. руб.

.

3. Метод Монте-Карло (метод статистических испытаний Имитационное моделирование случайных факторов)состоит из четырех этапов:

1. Построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохастических переменных.

2. Установление распределения вероятностей для стохастичес­ких переменных.

3. Установление интервала случайных чисел для каждой сто­хастической переменной и генерация случайных чисел.

4. Имитация поведения системы путем проведения многих ис­пытаний и получение оценки моделируемой характеристики си­стемы при фиксированных значениях параметров управления. Оценка точности результата.

Описание этапов:

Первый этап. Стохастическая имитационная модель (ИМ) не­которой реальной системы может быть представлена как динами­ческая система, которая под воздействием внешних случайных входных сигналов (входных переменных) изменяет свое состояние (случайные переменные состояния), что в свою очередь приводит к изменению выходных сигналов (выходных переменных):

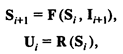
гдеF, R — вектор-функции;

I_i, U_i, S_i — векторы соответственно входных, выходных пере­менных и переменных состояния системы в так­товый момент моделирования i.

Имитационная модель — это экспериментальная модель систе­мы, в которой искусственно воспроизводятся случайности, име­ющие место в реальной системе. Она представляет собой совокуп­ность математических соотношений между входными, выходными переменными и переменными состояния в сочетании с алгорит­мической реализацией некоторых зависимостей.

Существует два подхода в имитационном моделировании ди­намических процессов.

Первый заключается в том, что весь период моделирования разбивается на равные промежутки времени (такты моделирова­ния) и анализ состояния системы, а также значений выходных переменных производится через одинаковые промежутки време­ни. При таком подходе возникает проблема выбора «правильной» продолжительности такта. Кроме того, не исключается появление тактов, в которых состояние системы по сравнению с предыдущим не изменилось.

При втором подходе величина такта моделирования не фик­сируется, моделирование в этом случае происходит в момент на­ступления одного из «существенных» событий. Например, при моделировании производственного процесса на предприятии та­кими событиями могут быть освобождение или начало загрузки станка, поступление на обработку детали, невыход на работу ста­ночника, исчерпание запаса необходимых комплектующих дета­лей на складе и др. Именно второй подход чаще всего использу­ется на практике и поддерживается современными языками мо­делирования.

Второй этап. Случайные величины, используемые в ИМ, мо­гут быть дискретными или непрерывными. В первом случае не­обходимо знать их распределения, во втором — плотности распре­делений. Эти зависимости могут быть известны из теории, опре­делены в результате специальных исследований либо заданы в качестве гипотезы. Точность модели (при прочих равных услови­ях) зависит от того, насколько точно заданы указанные распреде­ления (плотности распределений).

Третий этап. Моделирование случайных величин при компью­терных имитационных экспериментах производится с помощью датчика псевдослучайных чисел, предусмотренного в любом со­временном языке программирования. Обычно это датчик случай­ных чисел с равномерным распределением на интервале [0, 1]. Если известны вероятности наступления событий, то, используя такой датчик, можно отвечать на вопросы: «Какое из N возмож­ных событий произошло?» или «Какое значение приняла случай­ная величина?»

Предположим, что в ИМ используется случайная величина X, принимающая дискретные значения х₁, х₂,..., х_N с вероятностями соответственно p₁, p₂,..., p_N (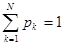). Получение некоторой реализации этой переменной в модели производится следующим образом.

Строится функция распределения случайной величины X. Ука­занная функция определяется посредством равенства F(X) = åp_k, в котором суммирование распространяется на все индексы, для которых х_k < X. С помощью датчика случайных чисел получают случайное число и из отрезка [0, 1].

Из равномерности распределения получаемых случайных чи­сел следует, что вероятность получения случайного числа из про­извольного интервала, включенного в [0, 1], равна длине этого интервала. Поэтому вероятность реализации Х = х_k равна веро­ятности попадания полученного от датчика случайного числа и в произвольный интервал длиной p_k на отрезке [0, 1]. Можно, та­ким образом, утверждать, что если очередное число и датчика удовлетворяет неравенствам 0 < и £ р₁, то имеет место реализа­ция Х = х₁, в случае p₁ < и £ p₁ + р₂ — реализация Х = х₂ и т.д. В общем случае для k = 2, ..., N: если < и £ 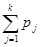, то Х = х_k.

Заметим, что границы указанных неравенств совпадают со зна­чениями построенной выше функции распределения F(X).

Удобнее, однако, иметь дело не с дробными значениями гра­ниц интервалов, в которые попадает случайное число и, а с их целочисленными значениями, тем более, что с помощью датчи­ков случайных чисел можно генерировать числа из любого диа­пазона. Чтобы получить целые значения границ интервалов, до­статочно умножить все p_k на 10^d, где d — целое, минимальное зна­чение которого равно максимальной точности (максимальному числу знаков после десятичной точки) чисел p_k, k = 1,..., N. На­пример, если {р_k} = {0,3; 0,153; 0,5; 0,047}, то минимальное зна­чение d равно 3 (все р_k нужно умножить на 1000). Таким образом, 10^d определяет длину интервала значений рассматриваемой слу­чайной величины в ИМ.

Четвертый этап. Точность статистических оценок параметров реальной системы зависит от числа наблюдений (объема выбор­ки). Погрешности в оценках обусловлены как статистическим характером самой модели, так и влиянием начальных данных (на­чального состояния имитационной системы), а также возможной автокорреляцией последовательных значений некоторого парамет­ра в процессе моделирования. Очевидно, что с увеличением чис­ла испытаний точность моделирования должна возрастать. Ввиду того что увеличение объема выборки связано с ростом затрат на моделирование, важно уметь определять минимальное число ис­пытаний, необходимое для достижения заданной точности оцен­ки с заданной вероятностью.

Широкое распространение получили два метода статистичес­ких испытаний. Один из них предполагает проведение достаточ­но большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования).

Другой метод заключается в реализации т независимых про­гонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если мы хотим получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

Пусть значения у_t (t = 1,..., Т) представляют собой результа­ты Т последовательных измерений значений случайной величи­ны y во время одного и того же сеанса имитации. Среднее по вре­мени значение у определяется выражением

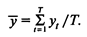
Обозначим через  математическое ожидание случайной вели­чины у. Тогда для достаточно большого T получаем

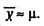
Оценка дисперсии (если временной ряд не является авто­коррелированным) имеет вид

где D(у) — дисперсия случайной величины у.

Для оценки качества результатов, полученных методом Мон­те-Карло при неизвестной дисперсии наблюдаемой случайной величины, предположим, что Z — характеристика, которая долж­на быть определена (вероятность события, математическое ожи­дание, дисперсия и т.п.), a x — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограни­ченности числа T проведенных наблюдений. В этих условиях мож­но говорить о вероятности p(|Z – x| < ) по отношению к инте­ресующей нас характеристике. Величина |Z – | представляет со­бой погрешность в оценке Z, a  — некоторый допустимый ее предел.

Из неравенства Чебышёва следует

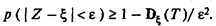
Из этого неравенства следует

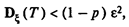
откуда при заданных р и  и при известной зависимости D_ (Т) можно найти предельно необходимое Т.

Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т, т.е.

где d не зависит от Т.

В начале имитационного процесса требуемое число наблюде­ний определить обычно не удается, поскольку d неизвестно. По­этому, как правило, эксперимент проводят в два этапа.

На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого можно уже определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.

Предельное число наблюдений Т₀ определяется формулой T₀ = d/[(1 – p)²].

При любом числе наблюдений больше Т₀ обеспечивается тре­буемая точность.

Примеры

Пример 1. Моделирование объема спроса на автомашины.

Наблюдения за объемом продаж автомобилей в салоне «ЛОГОВАЗ» в течение 200 дней показали, что величина спроса изменяется от 0 до 5 автомобилей в день. Частота реализации значений стохас­тической переменной приведена во втором столбце таблицы:

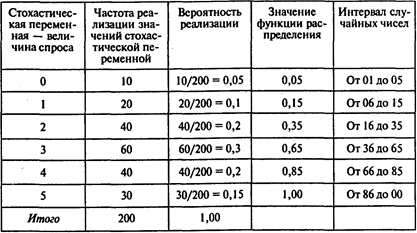
Постройте модель, позволяющую имитировать значение вели­чины спроса.

Решение. Построим функцию распределения величины спроса и интервалы случайных чисел для значений стохастической пере­менной. Соответствующие значения указаны в четвертом и пятом столбцах вышеприведенной таблицы.

Сымитируем спрос на автомашины в салоне «ЛОГОВАЗ» в те­чение 10 последующих дней (случайные числа из таблицы случай­ных чисел (Приложение 2) выбираем, начиная из верхнего лево­го угла и двигаясь вниз в первом столбце):

В результате получаем: 39 — спрос за 10 дней; 39/10 = 3,9 — средний ежедневный спрос.

Оценка 3,9 средней величины спроса, полученная в результате имитационного эксперимента, существенно отличается от значе­ния 2,95 — математического ожидания этой случайной величины. Однако эта разница уменьшается с ростом числа испытаний.

Пример 2. Моделирование очереди на разгрузку.

Груженые баржи, отправляемые вниз по Волге из индустри­альных центров, достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0, 1,..., 5 барж показана в таблице:

В этой же таблице указаны интегральные вероятности и соот­ветствующие интервалы случайных чисел для каждого возможного значения.

Аналогичная информация дана о числе разгружаемых барж:

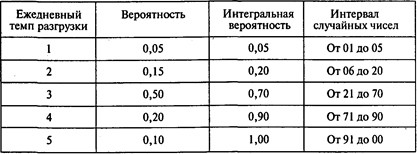
Постройте модель, позволяющую имитировать очередь на раз­грузку.

Решение. Проведем эксперимент, имитирующий очередь на разгрузку барж в порту Астрахани:

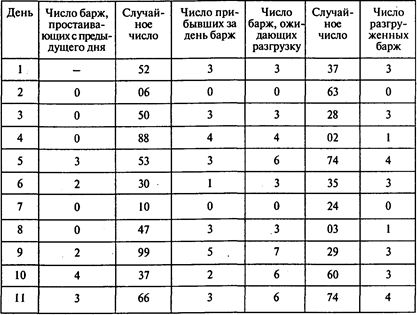
Окончание таблицы

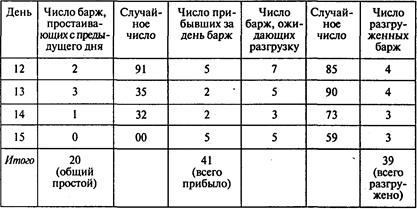
В результате эксперимента получены:

оценка среднего числа барж, простаивающих в течение суток, равная ²⁰/₁₅;

оценка среднего числа барж, прибывающих в течение суток, равная ⁴¹/₁₅;

оценка среднего числа барж, разгруженных в течение суток, равная ³⁹/₁₅.

Пример 3. Имитация стратегии резервирования.

Магазин электрооборудования продает электрические дрели. В течение 300 дней директор магазина Проводков регистрировал дневной спрос на дрели. Распределение вероятностей величины спроса показано в таблице:

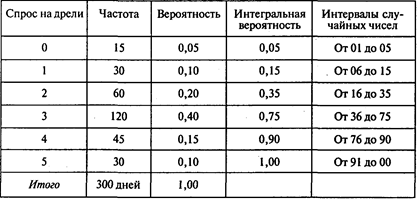
Когда Проводков делает заказ, чтобы возобновить свои запа­сы электрических дрелей, его выполнение происходит с лагом в 1, 2 или 3 дня. Это означает, что время восстановления запаса подчиняется вероятностному распределению. В следующей табли­це указаны сроки, вероятности сроков выполнения заказов и ин­тервалы случайных чисел, которые удалось определить на основе информации о 50 заказах:

Стратегия резервирования, которую хочет имитировать Про­водков, — делать заказ в объеме 10 дрелей при запасе на складе 5 шт. Проводков оценил, что каждый заказ на дрели обходится ему в 10 руб., хранение каждой дрели — в 5 руб. в день, одна упущен­ная продажа — в 80 руб. Цель эксперимента — оценить величину средних ежедневных затрат для этой стратегии управления запа­сами.

Решение. Реализуется четырехшаговый процесс имитации:

1. Каждый имитируемый день начинается с проверки, посту­пил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа (в данном случае — на 10 еди­ниц).

2. Путем выбора случайного числа генерируется дневной спрос для соответствующего распределения вероятностей.

3. Рассчитывается итоговый запас, равный исходному запасу за вычетом величины спроса. Если запас недостаточен для удовлет­ворения дневного спроса, спрос удовлетворяется, насколько это возможно. Фиксируется число нереализованных продаж.

4. Определяется, снизился ли запас до точки восстановления (в примере — 5 единиц). Если да, причем не ожидается поступле­ния заказа, сделанного ранее, то делается заказ.

Первый эксперимент Проводкова (объем заказа — 10 шт., точ­ка восстановления запаса — 5 шт.; СЧ — случайное число):

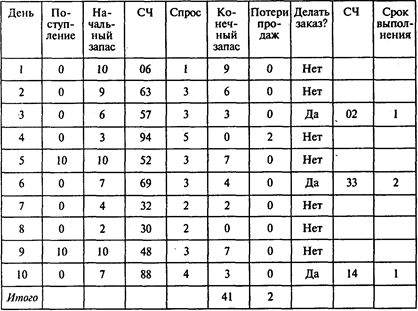
Результат имитационного эксперимента:

конечный суммарный запас — 41 единица;

средний конечный запас 41/10 =4,1 единицы;

число упущенных продаж — 2;

среднее число упущенных продаж 2/10 = 0,2 шт. в день;

среднее число заказов 3/10 = 0,3 заказа в день.

Определим три составляющие затрат:

Ежедневные затраты на заказы = Затраты на один заказ х Сред­нее число заказов в день = 10 • 0,3 = 3 руб.

Ежедневные затраты на хранение = Затраты на хранение одной единицы в течение дня х Средняя величина конечного за­паса = 5 • 4,1 = 20,5 руб.

Ежедневные упущенные продажи = Прибыль от упущенной продажи х Среднее число упущенных продаж в день = 80 • 0,2 = 16 руб.

Таким образом,

Общие ежедневные затраты = Затраты на заказы + Затраты на хранение + Упущенные продажи = 3 + 20,5 + 16 = 39,5 руб.