Проверка гипотез о законах распределения по методу К.Пирсона

Задача проверки гипотезы о виде закона распределения формулируется следующим образом.

Пусть в результате эксперимента получена случайная выборка 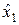, ,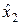…,и для неё выбран теоретический закон распределения, характеризуемый функцией распределения 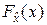или плотностью распределения .

Необходимо на основании обработки и анализа полученной выборки проверить гипотезу H₀ о том, что исследуемая случайная величина подчинена выбранному закону распределения.

В настоящее время существует ряд методов решения данной задачи, однако наибольшее распространение получил метод К. Пирсона. Достаточно употребляемыми являются также методы А.Н. Колмогорова и Н.В. Смирнова [4, 6, 12]. Указанные методы отличаются друг от друга видом меры рассогласования между статистическим и гипотетическим законами распределения. Так, в методах А.Н. Колмогорова и Н.В. Смирнова такой мерой является функция разности между статистической функцией распределения и функцией распределения 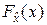гипотетического закона:

.

В методе К. Пирсона в качестве таковой используется функция разности между частотой и вероятностью попадания случайной величины в заданные интервалы:

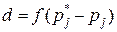, (7.1.6)

где j – номер интервала.

Рассмотрим метод К. Пирсона более подробно. Мера расхождения (7.1.6) в явном виде представляется суммой квадратов разностей между частотой и вероятностью попадания случайной величины в интервалы, на которые разбивается множество возможных значений этой величины:

, (7.1.7)

где r – число интервалов; l – номер интервала.

Коэффициенты c_l введены в выражение (7.1.7) для учёта того, что абсолютные значения разностей неравнозначны при различных значениях p_l. Действительно, одно и то же значение разности является малозначимым при большой величине p_l и представляет собой заметную величину, если вероятность p_l мала.

К. Пирсон показал, что коэффициенты c_l целесообразно брать обратно пропорциональными вероятностям p_l. При этом, если данные коэффициенты определять на основе выражения

, ,

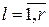то при больших значениях n закон распределения случайной величины

(7.1.8)

не зависит от вида распределения случайной величины и объёма выборки n, а зависит только от числа интервалов r. Кроме этого при увеличении n закон распределения случайной величины (7.1.8) приближается к распределению хи-квадрат [6].

Докажем это утверждение.

Рассмотрим случайную величину – число попаданий случайной величины в l-й интервал. Эта случайная величина распределена по биномиальному закону с характеристиками

, .

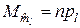Однако при достаточно большом n величину на основании теоремы Муавра-Лапласа можно считать распределённой по нормальному закону с теми же характеристиками. Выполняя нормирование случайной величины , получим

.

Нормированные случайные величины связаны между собой линейным соотношением

.

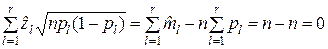На основании этого утверждаем, что случайная величина 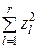будет приближённо следовать хи-квадрат (c²) распределению. Если эту случайную величину принять за показатель согласованности гипотезы, то получим равенство

. (7.1.9)

Преобразуем выражение (7.1.9), учитывая, что

и 1– p_l » 1 при больших значениях n:

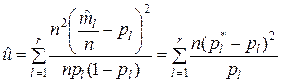(7.1.10)

или

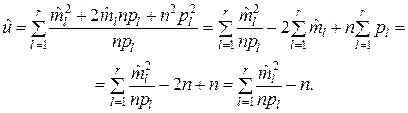(7.1.11)

Выражения (7.1.10) или (7.1.11) используются в зависимости от формы представления результатов наблюдения, т.е. в зависимости от того, являются ли исходными данными или m_l.

Как известно, распределение c² зависит от числа степеней свободы f = r – s, равного числу интервалов r минус число независимых условий (связей), наложенных на частоты . В формуле (7.1.10) предполагается наличие только одного условия

, (7.1.12)

которое накладывается всегда. Тогда принимаем s = 1 и число степеней свободы f = r – 1. Равенство (7.1.12) есть сумма вероятностей несовместных событий, образующих полную группу.

В случае, когда теоретическое распределение подбирается так, чтобы совпадали его математическое ожидание и оценка математического ожидания, полученная по результатам наблюдения, т.е.

,

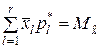число связей увеличивается на единицу. Следовательно, s = 2 и число степеней свободы f = r – 2. Если условие совпадения параметров теоретического и статистического распределения распространяется и на дисперсию

,

то s = 3, f = r – 3 и т.д.

Таким образом, число степеней свободы распределения c² зависит при проверке гипотез от условий проведения проверки, что необходимо учитывать, используя показатель согласованности гипотезы (7.1.13) или (7.1.14).

Можно показать, что при невыполнении гипотезы H₀ по мере возрастания n значение показателя согласованности 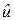будет неограниченно увеличиваться, т.е. кривая распределения сдвинута относительно кривой вправо. Поэтому в соответствии с рекомендациями предыдущего раздела в качестве критической целесообразно выбрать правостороннюю критическую область, рис.7.3.

Рис.7.3. Правосторонняя критическая область

В этом случае для определения критической границы u_a можно использовать приложение 7, в котором даны критические точки распределения c² в зависимости от уровня значимости a и числа степеней свободы f.

Порядок проверки гипотезы о виде закона распределения состоит в следующем.

1. Назначается уровень значимости a, и по таблице критических точек распределения c² (приложение 7) определяется критическая граница u_a. Входами в таблицу служат уровень значимости a и число степеней свободы f.

2. Результаты эксперимента представляются в виде интервального статистического (вариационного) ряда (табл.4.5), в котором m_l и – число и частота попаданий исследуемой величины в l-й интервал (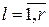) соответственно.

3. Вычисляются вероятности p_l попадания случайной величины , которая подчиняется гипотетическому закону распределения, в l-й разряд:

,

где – плотность распределения гипотетического закона. Очевидно, что должно выполняться условие

.

4. Рассчитывается значение u показателя согласованности гипотезы по формуле (7.1.10) или (7.1.11).

5. Проверяется условие u £ u_a. Если оно выполняется, то расхождение между экспериментальными данными и гипотезой H₀ полагается незначительным. В противном случае нулевая гипотеза отвергается.

Существенное достоинство метода К. Пирсона состоит в возможности его применения тогда, когда априорно известен лишь вид гипотетического распределения, но не известны его параметры. В этом случае параметры распределения заменяются оценками, которые используются в дальнейшем для вычисления вероятностей p_l, а число степеней свободы уменьшается на число заменяемых параметров. Метод К. Пирсона имеет следующие недостатки:

а) он применим только при большой выборке (n ³ 100), так как показатель согласованности подчиняется распределению хи-квадрат лишь при достаточно большом n;

б) результаты проверки в значительной степени зависят от способа разбиения выборки на интервалы, причём их число целесообразно делать не менее 8–10, а количество попаданий случайной величины в любой из интервалов должно быть не менее 5.

П р и м е р 7.3. В условиях примера 7.1 проверить согласованность теоретического и статистического распределений.

▼ Назначаем уровень значимости a = 0,05. Число степеней свободы f = 8 – 3 = 5. По таблице приложения 7 определяем критическую границу u_0,05 = 11,1.

Пользуясь теоретическим нормальным законом распределения с параметрами m = 0,168 и s = 1,448, находим вероятности попадания в разряды по формуле

,

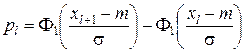где x_l, x_l+1 – границы l-го разряда. Значения функции Ф₁ находим в таблице приложения 3. Затем составляем расчётную таблицу 7.3.

Таблица 7.3

Расчётные данные (к примеру 7.3)

Jl	–4; –3	–3; –2	–2; –1	–1; 0	0; 1	1; 2	2; 3	3; 4
	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020
pl	0,012	0,052	0,142	0,244	0,264	0,181	0,076	0,021
		–0,002	0,002	0,022	–0,024	–0,005	0,012	–0,001
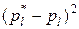
		4∙10–6	4∙10–6	484∙10–6	576∙10–6	25∙10–6	144∙10–6	10–6
		0,038	0,014	0,992	1,091	0,069	0,947	0,024

По формуле (7.1.10) находим значение показателя согласованности гипотезы

.

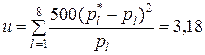Поскольку u = 3,18, u_0,05 = 11,1, то u < u_0,05 – гипотеза о нормальном распределении отклонений по вертикали при стрельбе в мишень принимается. ▲