Проверка гипотез о равенстве математических ожиданий

Пусть имеются две независимые случайные величины и 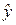, распределённые по нормальному закону. Эксперимент состоит в том, что над случайными величинами и 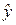осуществляется соответственно n и m независимых испытаний, в результате которых получаются случайные выборки 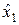, ,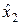…,и , ,…,. По этим выборкам определяются оценки математических ожиданий

, .

Требуется по полученным оценкам проверить гипотезу о равенстве математических ожиданий и .

Такая задача ставится потому, что, как правило, оценки математических ожиданий оказываются различными. Причина этого может быть двоякой: либо действительно отличны и оценки и математические ожидания, либо и одинаковы, а отличие оценок вызвано случайными причинами, в частности, случайным отбором вариантов выборки. Если окажется, что нулевая гипотеза справедлива ( = ), то различие в оценках и обусловлено случайными причинами, иначе различными являются математические ожидания. При решении данной задачи остановимся на том случае, когда дисперси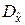и и 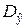известны.

В качестве показателя согласованности гипотезы выберем случайную величину

. (7.2.1)

Целесообразность выбора показателя согласованности вида (7.2.1) определяется следующими соображениями.

Введём в рассмотрение случайную величину

, (7.2.2)

которая, очевидно, распределена по нормальному закону и имеет числовые характеристики:

; ; .

Нормируем случайную величину (7.2.2) и получаем

. (7.2.3)

Случайная величина (7.2.3) подчинена нормальному закону распределения, параметры которого известны: = 0, 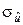= 1, что существенно упрощает процедуру проверки нулевой гипотезы. Действительно, если гипотеза H₀ справедлива ( = ), то случайная величина центрирована, откуда следует, что = 0. Так как выборки независимые, то 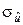= 1.

Критическая область строится в зависимости от вида конкурирующей гипотезы, которая может быть сформулирована тремя различными способами:

¹ ; > ; < .

Рассмотрим методику проверки гипотезы H₀ для каждого из приведённых способов формулировки конкурирующей гипотезы.

1. H₀: = ; H₁: ¹ .

В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости a.

Наибольшая мощность критерия достигается тогда, когда левая и правая критические точки u_a1, u_a2 выбраны так, что вероятность попадания показателя согласованности 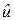в каждый из двух интервалов критической области равна a/2:

; .

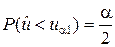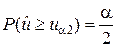Поскольку 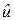– нормированная нормально распределённая случайная величина и её распределение симметрично относительно нуля, то критические точки также симметричны относительно нуля:

|u_a1| = |u_a2| = |u_a|.

Используя функцию нормированного нормального распределения (функцию Лапласа), вероятность попадания показателя согласованности в критическую область можно определить выражением

,

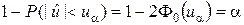откуда

. (7.2.4)

Двусторонняя критическая область будет определяться неравенствами u < –u_a, u > u_a. Таким образом, правило проверки гипотезы H₀ для рассматриваемого случая состоит в следующем.

а). Назначается уровень значимости a и в соответствии с формулой (7.2.4) по таблице приложения 4 определяются границы критической области u_a1 = –u_a, u_a2 = u_a.

б). На основе случайных выборок вычисляется наблюдаемое значение показателя u по формуле

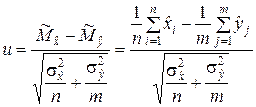. (7.2.5)

в). Проверяется условие |u| > u_a. Если оно выполняется, то гипотеза H₀ отвергается. В противном случае данные эксперимента не противоречат нулевой гипотезе.

П р и м е р 7.4. Производится контрольный отстрел двух партий снарядов, причём из первой партии проверяется 10 снарядов, а из второй – 15. В результате отстрела получены следующие оценки математических ожиданий отклонения точек попадания снарядов от точки прицеливания по дальности: для первой партии отклонение равно –0,8 км, для второй +0,4 км. Среднеквадратические отклонения по дальности для снарядов первой и второй партий известны и равны соответственно 2 и 1,5 км. Необходимо проверить гипотезу о совпадении проекций центров рассеивания на ось дальности в обеих партиях.

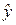▼ Пусть и – отклонение точек попадания снарядов от точки прицеливания по дальности соответственно для первой и второй партий.

По условию задачи n = 10, m = 15, = –0,8 км, = 0,4 км, = 2 км, 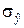= 1,5 км.

Задаёмся уровнем значимости a = 0,05 и в приложении 4 находим

u_a = t_1–a = t_g = t_0,95 = 1,96.

Используя формулу (7.2.5), вычисляем абсолютное значение показателя согласованности:

.

Так как |u| < u_a, нулевая гипотеза = не противоречит данным контрольного отстрела.

2. H₀: = ; H₁: > .

Такой случай возможен, если априорные сведения позволяют предположить, что > . В этом случае строят такую правостороннюю критическую область, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна a:

. (7.2.6)

Для того чтобы критическую точку найти с помощью функции Лапласа, перепишем выражение (7.2.6) в виде

.

Из предыдущего выражения получим

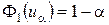
и, следовательно,

(7.2.7)

Правило проверки гипотезы для рассматриваемого случая.

а). Назначается уровень значимости a и в соответствии с (7.2.7) по таблице приложения 4 определяется величина u_a. При этом в таблицу следует входить со значением 1–2α,

б). Определяется величина u по формуле (7.2.5).

в). Проверяется условие u > u_a. Если оно выполняется, гипотеза H₀ отвергается, в противном случае принимается.

3. H₀: = ; H₁: < .

При указанной формулировке конкурирующей гипотезы левостороннюю критическую область строят так, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости: .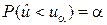

Учитывая, что показатель 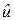имеет симметричное распределение относительно нуля, заключаем, что точка u_a1 симметрична такой точке u_a > 0, для которой , это значит u_a1 = –u_a. Следовательно, методика определения u_a1 полностью совпадает с методикой предыдущего случая, только полученное значение берётся с отрицательным знаком.

Правило проверки гипотезы также аналогично рассмотренному выше правилу, за исключением последнего пункта, а именно, если u < u_a1, нулевая гипотеза отвергается, в противном случае – принимается.

Выше предполагалось, что случайные величины и 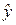распределены нормально, а их дисперсии известны. При этих предположениях показатель согласованности гипотезы распределён по нормальному закону с параметрами = 0, 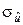= 1. Если хотя бы одно из предположений не выполняется, описанный метод проверки гипотезы о равенстве математических ожиданий неприменим. Однако при больших объёмах независимых выборок (³ 30 вариантов каждая) оценки математических ожиданий и дисперсий распределены приближённо нормально и закон распределения 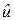можно считать близким к нормальному. В этом случае проверку гипотезы можно проводить по описанной выше методике, подставляя в формулу (7.2.5) оценки дисперсий, но к полученным результатам следует относиться с осторожностью.