Проверка гипотез о равенстве дисперсий

Проверка гипотез о равенстве дисперсий – одна из важнейших задач статистической обработки экспериментальных данных. На практике задача сравнения дисперсий возникает, если требуется сравнить погрешности показаний приборов, точность методов измерений и т.д.

Сформулируем задачу проверки гипотезы о равенстве дисперсий. Пусть имеются две случайные величины и 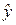, каждая из которых подчиняется нормальному закону распределения с дисперсиям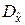и и 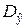. По независимым выборкам x₁, x₂,…,x_n и y₁, y₂,…,y_m найдены оценки дисперсий:

, (7.2.8)

где 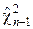, - хи- квадрат распределения с n – 1 и m – 1 степенями свободы соответственно.

Обычно полученные оценки различны, в связи с чем возникает вопрос, можно ли на основе обработки экспериментальных данных полагать, что 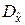= 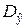(нулевая гипотеза).

Если нулевая гипотеза справедлива, то это означает, что выборочные дисперсии (7.2.8) представляют собой оценки одной и той же характеристики рассеивания генеральной совокупности и их различие определяется случайными причинами. В противном случае различие оценок существенно и является следствием того, что дисперсии генеральных совокупностей различны.

В качестве показателя согласованности гипотезы о равенстве дисперсий примем отношение большей оценки дисперсии к меньшей. Для определённости будет полагать 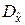> 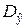, тогда

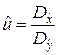. (7.2.9)

Учитывая оценки (7.2.8) при условии, что нулевая гипотеза справедлива, на основе отношения (7.2.9) получаем следующее выражение показателя согласованности:

.

Таким образом, показатель согласованности представляет собой случайную величину, подчинённую закону распределения Фишера со степенями свободы f₁ = n – 1 и f₂ = m – 1. Как известно, распределение Фишера зависит только от значений степеней свободы и уровня значимости, а от других параметров не зависит.

Критическая область в зависимости от вида конкурирующей гипотезы строится по-разному. Как и ранее, рассмотрим три вида конкурирующей гипотезы:

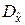¹ ; > ; < .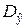

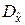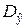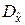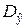Построение критических областей для каждого из этих видов осуществляется следующим образом.

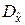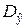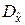1. H₀: = ; H₁: ¹ .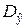

В этом случае строят двустороннюю критическую область, исходя из того, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна уровню значимости a. При этом достигается наибольшая мощность критерия проверки, когда вероятности попадания показателя согласованности в каждый из двух интервалов критической области будут одинаковы и равны a/2. Таким образом, при построении критической области должны выполняться следующие условия (рис.7.4):

Правая критическая точка u_a2 может быть найдена непосредственно по таблице критических точек распределения Фишера (приложение 5). При этом входами в таблицу будут величины a/2, f₁ = n – 1, f₂ = m – 1. В результате имеем

.

 

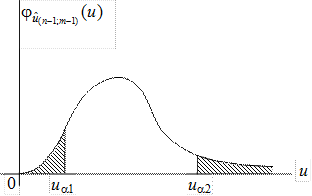
Рис.7.4. Двусторонняя критическая область

Однако левых критических точек данная таблица не содержит и найти непосредственно u_a1 невозможно. В связи с этим для нахождения левой критической границы u_a1 необходимо использовать следующий приём.

Рассмотрим события

F_{(n–1; m–1)} < F_a1 и .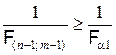

Так как эти события эквивалентны, то их вероятности равны:

.

Как известно [1], случайная величина также подчиняется закону распределению Фишера со степенями свободы f₁ = m –1, f₂ = n – 1. Поэтому значение 1/F_a1 может быть найдено как верхний 100(a/2)-процентный предел этого закона распределения:

.

Таким образом, для определения 1/F_a1 необходимо войти в таблицу критических точек распределения Фишера с аргументами a/2, f₁ = m –1, f₂ = n – 1. Значение левой критической границы определяется как величина, обратная значению, найденному по таблице.

Учитывая изложенное выше, правило проверки гипотезы о равенстве дисперсий можно сформулировать в следующем виде.

а). Назначается уровень значимости a и по таблице критических точек распределения Фишера находятся критические границы u_a1 и u_a2. При нахождении критической границы u_a2 в таблицу следует входить с аргументами a/2, f₁ = n – 1, f₂ = m – 1, а при определении критической границы u_a1 – с аргументами a/2, f₁ = m – 1, f₂ = n –1. В последнем случае табличное значение 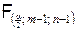используется для определения критической границы u_a1 из выражения

. (7.2.10)

б). Вычисляется значение показателя согласованности

. (7.2.11)

в). Проверяется неравенство

u_a1 < u < u_a2.

Если оно выполняется, то наблюдаемое значение показателя согласованности попадает в область допустимых значений. В этом случае делается вывод об отсутствии существенного различия между сравниваемыми дисперсиями и гипотеза H₀ принимается. Если u < u_a1 или u > u_a2, то нулевая гипотеза отвергается.

П р и м е р 7.5. При исследовании стабилизатора напряжения проведено семь испытаний и получена оценка дисперсии выходного напряжения, равная 0,06 B². После доработки стабилизатора проведено ещё 13 испытаний, в результате чего оценка дисперсии выходного напряжения стала равна 0,10 B². Есть ли основание полагать, что в результате доработки точность стабилизатора не изменилась?

▼ Обозначим 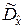= 0,10 В², = 0,06В². Тогда n = 13, m = 7. Задаёмся уровнем значимости a = 0,10 и в приложении 5 находим u_a2 для a/2 = 0,05, f₁ = n – 1 = 12, f₂ = m – 1 = 6. Также находим u_a1 для a/2 = 0,05, f₁ = m – 1 = 6, f₂ = n – 1 = 12. Получаем u_a2 = 4, F_(0,05;6;12) = 3 и, следовательно, u_a1 = 0,33.

Значение показателя согласованности по формуле (7.2.11):

.

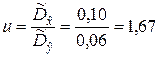Так как u_a1 < u < u_a2, то гипотеза H₀ о том, что доработка не повлияла на точность стабилизатора напряжения, принимается. ▲

2. H₀: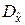 = 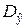; H₁: > .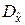

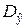В этом случае строят правостороннюю критическую область таким образом, чтобы вероятность попадания в эту область показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости:

.

Критическую точку находят по таблице критических точек распределения Фишера, используя в качестве аргументов a, f₁ = n – 1, f₂ = m – 1. Наблюдаемое значение показателя согласованности определяется по формуле (7.2.11). Если u < u_a, то нет оснований отвергнуть нулевую гипотезу, в противном случае она отвергается.

3. H₀: 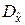= 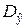; H₁: < .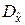

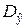В данном случае строят левостороннюю критическую область таким образом, чтобы

.

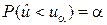Критическая точка находится по таблице критических точек распределения Фишера на основе отношения

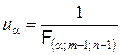. (7.2.12)

В знаменателе (7.2.12) – табличное значение, найденное при аргументах a, f₁ = m – 1, f₂ = n – 1.

Наблюдаемое значение показателя согласованности определяется по формуле (7.2.11). Если u > u_a, то нулевая гипотеза принимается, в противном случае она должна быть отвергнута.

В заключение следует отметить, что показатель согласованности гипотезы (7.2.9) можно использовать для сравнения дисперсий и в том случае, когда для одной из дисперсий найдена не оценка, а её точное значение. В этом случае число степеней свободы закона распределения Фишера в числителе или знаменателе выражения (7.2.9) следует устремить к бесконечности, в остальном методика проверки гипотезы остаётся прежней.

П р и м е р 7.6. Из партии снарядов с известной характеристикой рассеивания по дальности 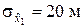испытываются 10 снарядов, хранившихся без специальной тары. Есть ли основание полагать, что по причине такого хранения рассеивание снарядов по дальности возросло, если в результате испытаний получена оценка ?

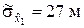▼ В данном примере кривая распределения характеристики 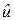при конкурирующей гипотезе смещена влево, поэтому в качестве критической выбираем левостороннюю область.

Пусть a = 0,05, тогда для определения u_a входим в таблицу приложения 5 со значениями a = 0,05, f₁ = m – 1 = 9, f₂ = ¥. Получим F_(0,05;9;∞) = 1,88, следовательно,

.

Вычисляем значение показателя согласованности

.

Так как u > u_a и значение показателя согласованности попало в область допустимых значений, то нет оснований утверждать, что в результате хранения без специальной тары рассеивание снарядов по дальности возросло.

▲