Вывод давления идеального газа из молекулярно-кинетических представлений

Вывод давления идеального газа из молекулярно-кинетических представлений.

2. Уравнение состояния ИГ. Изопроцессы. При обычных условиях (т.е. при комнатной температуре и атмосферном давлении) параметры состояния таких газов, как…

Согласно закону равнораспределения среднее значение энергии одной молекулы <e> будет (при той же температуре) тем больше, чем сложнее молекула, чем больше у нее степеней свободы. При определении <e> нужно учесть, что колебательная степень свободы должна обладать вдвое большей энергетической емкостью по сравнению с поступательной или вращательной. Поэтому на каждую колебательную степень свободы должны приходиться в среднем две половинки kT — одна в виде кинетической энергии и одна в виде потенциальной. Таким образом, средняя энергия молекулы должна равняться , где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=nпост + nвращ + 2nколеб.

N₀-кол-во атомов в молекуле.

Число степеней свободы=3N₀

Делятся на

1)поступательные n=3

2)вращательные n=3

3)колебательные n=3N₀-6

Лин.молекула: n_вращ=2

n_{колебат}=3N₀-5

4. Число степеней свободы многоатомной молекулы. Энергия многоатомной молекулы идеального газа.

Числом степеней свободы механической системы называется число независимых величин, с помощью которых может быть задано положение системы.

В физике выделяют три “вида” степеней свободы:

1) поступательная

2) вращательная

3)колебательная

Закон равнораспределения гласит о том, что на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная (1/2)kT.

Твердое тело имеет 6 степеней свободы (3 вращательные и 3 поступательные см. рис. выше), точка имеет 3 степени свободы (поступательные).

Рассмотрим молекулу состоящую из N атомов. В этом случае количество степеней свободы равняется 3N (положение каждой из N точек – атомов должно быть задано тремя координатами).

3N
поступательные	вращательные	колебательные
n=3	N=3	n=3N-6
n=2 (линейная молекула)	n=3N-5 (линейная молекула)

Среднее значение энергии одной молекулы <e> будет (при той же температуре) тем больше, чем сложнее молекула, чем больше у нее степеней свободы. При определении <e> нужно учесть, что колебательная степень свободы должна обладать вдвое большей энергетической емкостью по сравнению с поступательной и вращательной. Это объясняется тем, что поступа тельное и вращательное движение молекулы связано с наличием только кинетической энергии, в то время как колебательное движение связано с наличием и кинетической, и потенциальной энергии, причем для гармонического осциллятора среднее значение кинетической и потенциальной энергии оказывается одинаковым т.е. в среднем две половинки kT.

Таким образом <e>=(i/2)kT, где i=n_пост+n_вр+2n_колеб

Молекулы идеального газа не взаимодействуют между собой. Поэтому внутреннюю энергию одного моля идеального газа можно найти, умножив постоянную Авогадро на среднюю энергию одной молекулы:

5. Внутренняя энергия газа. Работа.

6. Количество теплоты. Первое начало термодинамики.

При совершении одним телом работы А над другим, равно как и при сообщении одним телом другому теплоты Q, эти тела обмениваются внутренней энергией — энергия одного из тел увеличивается, а энергия другого на столько же уменьшается. Это следует из закона сохранения энергии. В термодинамике этот закон принято называть первым началом и записывать следующим образом: Q=U₂—U₁+A (1.5). Здесь U₁ и U₂ - начальное и коночное значения внутренней энергии тела (или системы тел), А - работа, совершенная телом (или системой), Q — количество сообщенной телу (системе) теплоты. Словами первое начало термодинамики формулирует! следующим образом: количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и па совершение системой работы над внешними телами.Подчеркнем, что речь идет о разности конечного и начального значений внутренней энергии.

При вычислении совершенной системой работы или полученной системой теплоты обычно приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует весьма малому (в пределе — бесконечно малому) изменению параметров системы. Уравнение (1,5) для элементарного процесса имеет вид D¢Q=DU+D¢A ,где D¢Q элементарное количество теплоты, D¢A — элементарная работа и DU — приращение внутренней энергии системы в ходе данного элементарного процесса. Весьма важно иметь в виду, что D¢Q и D¢A нельзя рассматривав как приращения величии Q и А. Соответствующее элементарному процессу D какой-либо величины f можно рассматривать как приращение этой величины только в том случае, если åDf, соответствующая переходу из одного состояния в другое, не зависит от пути, по которому совершается переход, т.е. если величина f является функцией состояния. В отношении функции состояния можно говорить о ее «запасе» в каждом из состояний. Например, можно говорить о запасе внутренней энергии, которым обладает система в различных состояниях.

7. Теплоемкость идеального газа при постоянном объеме

Теплоемкостью какого-либо тела называется величина, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин. Аналитически это определение записывается следующим образом: Если нагревание производится при постоянном объеме, то тело не совершает работы над внешними телами и, cледователь- но, вся теплота идет на приращение внутренней энергии тела: d¢Q_V=dU. 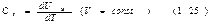Отсюда следует, что молярная теплоемкость любого вещества при постоянном объеме равнаВ термодинамике подобные формулы принято записывать в виде Символ частной производной, снабженный индексом V, указывает на то, что при дифференцировании функции U_M по переменной Т объем предполагается постоянным.

8. Теплоемкость идеального газа при постоянном давлении.

Теплоемкость при постоянном давлении Ср бывает больше, чем C_V, потому что при p=const нагреваемое тело расширяется и часть подводимой теплоты расходуется на совершение работы над внешними телами.

Внутренняя энергия определяется с точностью до произвольной аддитивной постоянной. Поэтому константу в выражении для U_M можно отбросить. В результате получается формула Внутренняя энергия — величина аддитивная. Следовательно, внутренняя энергий массы газа m будет равна Напишем уравнение d¢Q=dU + pdV для моля газа, предположив, что теплота сообщается газу при постоянном давлении: d¢Q_P=dU_M + pdV_M Разделив это выражение на приращение температуры dT, которое получает газ при сообщении ему теплоты d¢Q_P, придем к формуле для молярной теплоемкости газа при постоянном давлении: 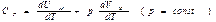Согласно формуле (1.25) слагаемое dU_M/dT равно молярной теплоемкости при постоянном объеме. Учтя это и использовав применяемый в термодинамике способ записи формул, придём к соотношению

9. Уравнение адиабаты идеального газа.

Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим. Чтобы найти уравнение адиабаты идеального газа, т. е. уравнение, связывающее параметры состояния идеального газа при адиабатическом процессе, воспользуемся уравнением первого начала термодинамики, подставив в него выражение 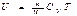дляU: 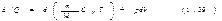В отсутствие теплообмена с внешней средой d¢Q = 0. Поэтому для адиабатического процесса уравнение (1.39) упрощается следующим образом:(мы произвели очевидные преобразования). Взяв дифференциал от обеих частей уравнения pV=(m/M)RT, придем к равенству

Умножим уравнение (1.40) на отношение R/C_V и сложим его с уравнением (1.41). В результате получим g pdV+Vdp=0 (1.42), где g=1+R/C_V=C_P/C_V. Наконец, разделим (1.42) на произведение pV: Левую часть этого уравнения можно представить в виде d ln(pV ^g). откуда следует, что pV^g=const. Мы получили уравнение адиабаты идеального газа в переменных р и V. Его называют уравнением Пуассона. Представив уравнение (1.44) в виде pV×V^g^-1=const и учтя, что произведение рV пропорционально T, придем к уравнению адиабаты идеального газа в переменных T и V: TV^g^-1=const (1.45) (константы в формулах (1.44) и (1.45) имеют, разумеется, неодинаковое значение).

10. Работа, совершаемая газом при различных процессах.

Если известна для некоторого обратимого процесса зависимость давления газа от объема, т.е. функция p=f(V) работа, совершаемая в ходе этого процесса, вычисляется путем интегрирования:Здесь V₁ и V₂ — объем газа в начальном и конечном состояниях. Чтобы произвести интегрирование, нужно выразить р через V. Для этого воспользуемся связью междур и V при различных процессах.

Уравнение политропы идеального газа pVⁿ=const можно написать следующим образом: pVⁿ=p₁V₁ⁿ=p₂V₂ⁿ, где р₁V₁ и р₂,V₂ — значения давления и объема газа соответственно в первом (начальном) и втором (конечном) состояниях, р и V — давление и объем в любом промежуточном состоянии. Выразим в соответствии с этим соотношением давление газа через его объем и значения параметров в начальном состоянии: p=p₁V₁ⁿ/Vⁿ

Подстановка этого выражении в (1.54) дает: Рассмотрим сначала случай n¹1: тогда интеграл в (1.55) равен 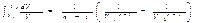Подставив это значение интеграла в (1.55) и произведя несложные преобразования, получим 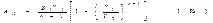Полученное выражение можно преобразовать, воспользовавшись тем, что, какой бы процесс ни происходил с идеальным газом, его параметры связаны уравнением состояния. В частности, это справедливо и для начального состояния: p₁V₁=(m/M)RT₁ (1.57). Приняв во внимание (1.57), напишем выражение (1.56) в виде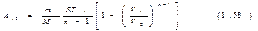

Выражения (1.56) и (1.58) дают работу, совершаемую идеальным газом при любом политропическом процессе, кроме изотермического (соответствующего n=1). В частности, при адиабатическом процессе 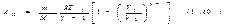Чтобы вычислить работу идеального газа при изотермическом процессе, заменим давление в формуле (1.54) его выражением через другие величины в соответствии с уравнением состояния. В результате получим (Т можно вынести за знак интеграла, поскольку она постоянна)

Итак, работа, совершаемая идеальным газом при изотермическом процессе, равна 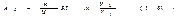При изобарическом процессе работа, совершаемая любым телом, в том числе и идеальным газом, равна, как следует из (1.54), A₁₂=p(V₂—V₁) (1.62). Тот же результат получается, если положить в (1.56) n равным нулю. В заключение отметим, что при изохорическом процессе работа равна нулю, что справедливо для любых тел.

11. Вероятность. Функция распределения и ее свойства.

Т. к. dw_v=f(v)dv=φ(v_x)dv_xφ(v_y)dv_yφ(v_z)dv_z → ,

где φ(v_x) – функция распределения по v_x. Вероятности того, что молекула имеет проекции скорости в интервалах (v_x, v_x+dv_x), (v_y, v_y+dv_y), (v_z, v_z+dv_z), являются независимыми, поэтому в соответствии с теоремой об умножении вероятностей независимых событий можно записать:

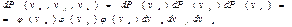
Отсюда получаем, что f(v)=φ(v_x)φ(v_y)φ(v_z).

Откуда 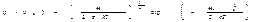. Функция нормирована на единицу. Т.е.

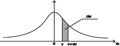
График зависимости φ(v_x) от v_x

12. Функция распределения Максвелла для вектора скорости в декартовых координатах.

Т.к.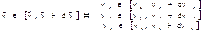,то

Для выяснения способа, которым можно количественно описать распределение молекул по значениям скорости, воспользуемся следующим приёмом. Возьмем в “воображаемом” пространстве, которое мы будем называть v-пространством (пространством скорости), прямоугольные координатные оси, по которым станем откладывать значения v_x, v_y и v_z отдельных молекул (имеются в виду компоненты по осям x, y и z, взятым в обычном пространстве). Тогда скорости каждой молекулы будет соответствовать точка в этом пространстве. Из-за столкновений положения точек будут непрерывно меняться, но их плотность в каждом месте будет оставаться неизменной (т.к. рассматривается равновесное состояние газа). Вследствии равновесности всех движений расположение точек относительно начала координат будет сферически симметричным, следовательно, плотность точек v-пространстве может зависить только от модуля скорости v. Отсюда получаем:

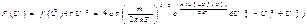
13. Функция распределения Максвелла для модуля скорости.

Найдем dw или относительное число молекул, модуль скорости которых заключен в интервале [v, v+dv]. Таким молекулам соответствуют все точки попадающие в шаровой слой с радиусами v и v+dv (рис. 1). Объем этого слоя равен V=4πv²dv. Объемная плотность вероятности во всех точках слоя одинакова, поэтому по теореме о сложении вероятностей, вероятность попадания в этот слой:

DP=f(v)·4πv2dv.

F(v)=dP/dv=4πv2f(v)→ F(v)= Это и есть закон распределения Максвелла по модулю скорости. Функция…

Энтропией (статистическое определение) называется величина S = k*lnΩ. Энтропия – мера беспорядка, т.е состояниям с большим беспорядком соответствует большая вероятность. Величина возрастания энтропии в замкнутой макросистеме может служить мерой необратимости процессов, протекающих в системе. В предельном случае, когда процессы обратимы, то энтропия не изменяется. Свойства энтропии

1. Энтропия – аддитивная функция состояния, т.е. S = S₁ + S₂, энтропия полного цикла равна нулю.

2. Энтропия замкнутой системы не убывает:

3. Теорема Нернста

21. Коэффициент полезного действия (к.п.д.) тепловой машины.

Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η (« эта»). η = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде:

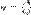x 100 %, где А — полезная работа, а Q — затраченная работа. В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии. КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя, к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле

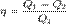,где Q₁ — количество теплоты, полученное от нагревателя, Q₂ — количество теплоты, отданное холодильнику. Наибольшим КПД обладают тепловые двигатели, работающие по циклу Карно.

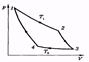
22. Цикл Карно. КПД цикла Карно. Теоремы Карно.

Рассмотренный Карно тепловой двигатель состоял из нагревателя с температурой Тi, холодильника с Т₂ и рабочего тела, т.е. устройства, способного получать тепло и совершать работу. Под рабочим телом пока будем понимать идеальный газ в цилиндре с поршнем. Карно рассмотрел цикл из двух изотерм и двух адиабат. При изотермическом расширении 1-2 газ находится в контакте с нагревателем (T1). Пусть при этом газ получает тепло Q1. На изотерме 3-4 газ отдает тепло Q₂ холодильнику (T₂). КПД двигателя: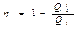

Данный цикл является обратимым (если его проводить бесконечно медленно). Он может быть проведен в обратном направлении, и при этом газ совершает отрицательную работу, нагреватель получает обратно тепло Q_1; холодильник отдает газу тепло Q₂, которое он получил в прямом цикле. Именно так в принципе работает любой бытовой холодильник.

Дальнейшие рассуждения проще всего провести, изобразив цикл Карно не на диаграмме р, V, а на диаграмме S, Т (энтропия — температура). На этой диаграмме цикл Карно имеет вид прямоугольника (рис. 3.6). Изотермы изображаются прямыми 1-2 и 3-4, адиабаты — прямыми 2-3 и 4-1. Согласно (3.3) полученное тепло Qi = T'i(S₂ - Si) и равно площади под 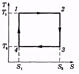отрезком 1-2.

23. Закон Кулона.

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

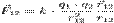где 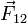— сила, с которой заряд 1 действует на заряд 2; q₁,q₂ — величина зарядов; 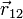— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — r₁₂); k — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

В СИ 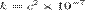= 8,9875517873681764×10⁹ (Кг·м³)/(Кл²·c²) (или Ф⁻¹·м) и записывается следующим образом:

24. Напряженность электрического поля. Электрические силовые линии. Принцип суперпозиции полей.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равна отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: . Также иногда называется силовой характеристикой электрического поля. Математически зависимость вектора 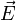от координат пространства сама задаёт векторное поле. Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр). Для системы СИ Используя потенциалы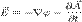К примеру, для точечного заряда, исходя из закона Кулона Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю: . В силу центральной симметрии поля точечного заряда: .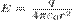

Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м², перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным. При положительном заряде, образующем поле, вектор напряженности направлен вдоль радиуса от заряда, при отрицательном - вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.

Напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.

В случае двух электрических полей с напряженностями Е₁ и Е₂ модуль вектора напряженности равен:

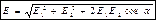
, (17)

где a — угол между векторами E₁ и E₂.

25. Работа сил электростатического поля.

Работа перемещения заряда.На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
F = q E. При перемещении заряда на отрезке dl силами поля совершается работа dA = Fdl =q E dl cos (E, dl). При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна. Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого . Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl). Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении. Для электрического поля, созданного системой зарядов Q₁, Q₂,¼, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:

.Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.

Циркуляция вектора напряженности электрического поля.Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

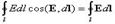Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю циркуляция вектора напряженности, т.е. .

26. Потенциальная энергия точечного заряда в электрическом поле.

работа консервативных сил совершается за счет убыли потенциальной энергии, значит выражение (18) можно представить так:

(19)

Т.е. потенциальная энергия заряда в поле заряд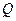а равна (20)

Если поле создается системой n зарядов 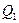, , 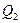…, , 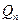то потенциальная энергия заряда , который находится в поле этих зарядов, будет равна сумме потенциальных энергий каждого из зарядов в отдельности: