Общий алгоритм решения матричной игры с помощью линейного программирования

 

1. Исследуем предложенную матричную игру на величину цены игры, т.е. определяем нижнею чистую цену игры a и верхнею цену игры b.

 

Возможны следующие случаи:

1) Þ есть седловая точка и цена игры определяется седловым элементом.

2) или Þ или преобразование матричной игры не нужно, необходимо составить соотношения из следствия теоремы Фон-Неймана (1), (2).

3) 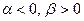Þ цена игры , либо

 

Необходимо преобразовать исходную матрицу, возможны два случая:

1) прибавить по всем элементам матрицы число к, которое определяется как из отрицательных элементов максимум.

2) из каждого элемента вычисть наибольшее положительное значение матрицы.

 

2. На основе следствий из теоремы Фон-Неймана записываются соотношения для первого или второго игрока:

Для первого игрока:

 

(1)

(2)

Для второго игрока:

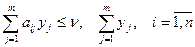
3. Приводят задачу определения к задаче линейного программирования, где линейная форма минимизируется (для первого игрока).

Если решают задачу отношений игрока, то получают задачу линейного программирования с максимальной линейной формы.

При этом получают ограничения для первого игрока:

для второго игрока:

Запишем для первого игрока эти ограничения подробнее:

 

4. Ввод базисных переменных: для первого игрока — отрицательная переменная такая, чтобы предложенное неравенство превратилось в равенство (ограничения).

5. Решают задачу линейного программирования.

При этом первой исключается переменная (исходные: ) имеющая максимальную сумму коэффициентов в системе ограничений. Для этого используются уравнения с минимальным отношением свободного члена к коэффициенту при выбранной переменной 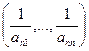. Этот процесс продолжается до тех пор, пока не останутся одни базисные переменные.

В результате получается линейная форма (для первого игрока):

6. Определяют цену игры

7. Определяют в ходе решения, по известному определяют , т.е. определяются компоненты смешанной стратегии первого игрока.

8. Определяются компоненты смешанной стратегии второго игрока из линейной формы, которая на последнем шаге решения задачи линейного программирования сводится к следующему виду:

 

 

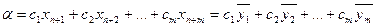
Лекция № 11

 

Многошаговые игры

Игра называется многошаговой, если хотя бы один из игроков делает больше одного хода.

Существует два вида моделей:

1. игра описывается последовательностью матриц;

2. игра описывается матрицами, элементы которых в свою очередь могут быть матрицами.

Например: возьмем матричную игру А:

 

A =, где

 

a₁₁, a₂₂ — действительные числа, определяющие выигрыш первого игрока, если игроки одновременно выбирают соответственно свои первые или вторые стратегии; A₁, A₂ - игры, которые необходимо разыгрывать, если, соответственно, первый игрок выбирает свою первую стратегию, а второй - вторую, или наоборот, первый игрок выбирает вторую стратегию, а второй - первую.

Игры A₁, A₂, в свою очередь, могут не заканчиваться определением выигрыша первого игрока в каждой игре на втором шаге, а требовать розыгрыша одной или нескольких игр на третьем шаге.

Пример: Рассмотрим в качестве примера трехшаговую игру со следующими матрицами:

 

 

Для оптимального поведения в такой многошаговой игре необходимо вначале определить цены v₃, v₄ игр A₃, A₄, затем определить цены v₁, v₂ игр

 

 

И после этого решить матричную игру

 

Для решения многошаговой матричной игры, имеющейся в качестве элементов матрицы, необходимо начинать решение с последнего шага. Решив матричные игры на последнем шаге, и получив значение цен игр, эти значения представляют в матрицы предшествующего шага. Так продолжается до тех пор, пока не будет получена числовая матрица для первого шага, затем определяют цену игры на первом шаге и оптимальные стратегии.

Более сложная ситуация возникает когда неизвестное количество шагов.

В этом случае получение решений существенно усложняется.

Способ получения решений — получение рекурсивных процедур.

 

Пример: Игра инспектирования. Участвуют два игрока: первый — нарушитель, второй — инспектор.

Нарушитель может действовать в интервале времени 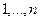и может совершить только одно нарушение. Инспектор совершает проверку один раз. Если инспектор и нарушитель действуют в один интервал времени, то считается, что нарушитель пойман и он наказывается штрафом в одну единицу. Если нарушитель и инспектор действуют в разные интервалы времени, то нарушитель принимает некоторые благи величиной +1.

Если нарушитель бездействует, то он ничего не приобретает.

Если нарушитель и инспектор бездействуют на всех шагах, то игра переносится на следующие шаги.

Требуется определить цену игры и оптимальное поведение обоих игроков.

	I II

 

 

I стратегия — активное действий;

II стратегия — пассивное действие.

 

На последнем шаге матрица будет вычисляться следующим образом (если оба бездейственны).

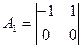
— цена одношаговой игры;

— цена двухшаговой игры;

— цена трехшаговой игры;

— цена четырехшаговой игры;

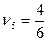— цена пятишаговой игры.

 

 

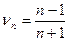
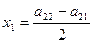
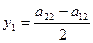
Возьмем стратегию :

 

Эти формулы справедливы при .

Рассмотрим на первом шаге:

вероятность действия у инспектора и у нарушителя — минимален, с каждым шагом вероятность увеличивается. Это для игр .

В случае, если размерность матрицы больше чем и нет седловой точки, то решать их сложно.

 

Игры Блотто

 

Обобщением является игры Бореля. Самая простая игра Бореля. Каждый из игроков выбирает по 3 неотрицательных числа.

Числа располагают в определенном порядке, выигрывает тот, у кого два числа окажутся большими.

Дополнительными есть две фирмы с одинаковым капиталом . Фирмы включают свои средства в три разных рынка.

Если вложения фирм в эти рынки таковы, что большей части (двух) рынков преобладает одна из фирм, в течении некоторого интервала времени, то она вытесняет конкурента с этих рынков и побеждает в конкурентной борьбе.

 

1) — первое обобщение Бореля.

2) второе обобщение Бореля — функции, зависящие от денег:

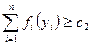
Игра Бореля может быть игрой на разорение.

В этом случае на первом шаге обе фирмы (оба игрока) имеют одинаковые ресурсы, а на последующих шагах ресурсы проигравшей фирмы уменьшаются на величину цены игры, или на величину, определяемую каким-то образом через цену игры.

 

 

Общее определения:

Играми на разорение над многошаговые игры, в которых каждый игрок начиная игру имеет ограниченные ресурсы и с каждым шагом ресурсы проигравшего игрока уменьшается на цену игры, либо на 1, либо на величину, определяемую ценой игры.

Игра на разорение может быть сформулирована и как игра на выигрыш — игроки начинают игру с нулевыми ресурсами и ресурсы выигравшего игрока увеличиваются на “1”, либо на цену игры, либо на значение, определяемое ценой игры.

 

Пример: Игра на разорение Блотто.

Имеется два игрока: А и Б, которые взаимодействуют на n участках взаимодействий.

Выигрыш (платеж) в этой игре первый игрок на i-ом рынке определяется функцией , где и 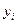— соответственно вложения фирм (игроков) А и В в i-й рынок. При этом выполняется условие:

— сумма ресурсов

При этом будем предполагать, что ресурсы таковы, что они могут дробиться на целое число единиц (т.е. до 4).

 

 

Стратегии	(3, 0)	(0, 3)	(2, 1)	(1, 2)
(4, 0)	(7, 0)	(4, 3)	(6, 1)	(5, 2)
(0, 4)	(4, 3)	(7, 0)	(5, 2)	(6, 1)
(3, 1)	(4, 3)	(3, 4)	(6, 1)	(4, 3)
(1, 3)	(3, 4)	(4, 3)	(4, 3)	(6, 1)
(2, 2)	(2, 5)	(2, 5)	(5, 2)	(5, 2)

 

Рассмотрим игру дальше:

 

Стратегии	(2, 0)	(0, 2)	(1, 1)
(5, 0)	(7, 0)	(5, 2)	(6, 1)
(0, 5)	(5, 2)	(7, 0)	(6, 1)
(4, 1)	(7, 0)	(4, 3)	(6, 1)
(1, 4)	(4, 3)	(7, 0)	(6, 1)
(3, 2)	(7, 0)	(5, 2)	(7, 0)
(2, 3)	(5, 2)	(7, 0)	(7, 0)

 

Если ресурсы одного из игроков превосходит ресурсы другого, то игрок получает платеж в виде суммы средств, вложенных противником и вложенных им самим.

Если ресурсы одинаковы, то каждый из противников возвращает свои затраты. Это же происходит и в том случае, если противник не вложил в рынок никаких ресурсов.

 

 

Лекция № 12

 

Многокомпонентная игра Бижуэлла на истощение

 

n стратегий   m стратегий

Есть два игрока, первый игрок имеет ресурсы:

 

 

Игра многошаговая, на каждом шаге(i,j):

— если это первая партия, то они уменьшаются на значение .

Выиграл тот игрок, который первый добьется нулевого значения, хотя бы одного из ресурсов другого игрока, т.е. по каждому ресурсу есть матрица истощения.

Игра многошаговая, но не бесконечная.

Бесконечные антагонистические игры будем рассматривать игры, обобщающие матричные игры.

 

 

Игра называется бесконечной, если хотя бы у одного из игроков имеется бесконечное число возможных стратегий. Обычно рассматриваются стратегии из множеств, которые представляют собой открытый или замкнутый интервал:

Если а и b изменяются в пределах, то приходиться рассматривать каждый раз другую игру.

 

0 1 y1 ….. ym

Также возможны случаи [0;1]; [0;1], тогда возникает бесконечная антагонистическая игра на единичном квадрате.

 

 

 

Для неправильной игры:

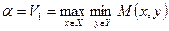
Если , имеем седловую точку и решение бесконечной антагонистической игры в чистых стратегиях.

Если нет решения в чистых стратегиях, то в общем случае не гарантируется, что есть решения в смешанных стратегиях; если функция 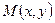имеет разрывы, то решение в смешанных стратегиях может отсутствовать.

 

 

Основная теорема теории непрерывных игр на единичном квадрате

 

Всякая антагонистическая бесконечная игра двух игроков с непрерывной функций выигрышей 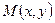на единичном квадрате имеет решение в чистых или стратегиях.

Для описания вероятности появления тех или иных стратегий первого и второго игрока, используются интегральные законы распределения вероятности.

Для первого игрока —

Для второго игрока —

С точки зрения интегрального закона, функция выражает вероятность того, что случайная величина Х примет значение меньше чем х, аналогично и для второго игрока.

Мы рассматриваем случай непрерывных и дифференциальных функций F и G.

Получаем функции плотности распределения вероятностей.

С помощью дифференциала можно определить вероятности появления стратегий на каких-то конечных, в том числе и малых интервалах изменения x и y.

 

Если мы имеем , это выигрыш первого игрока в том случае, если он применяет свою стратегию х, а второй игрок придерживается стратегии Y.

 

1) Если рассматривать случай:

то получим некоторый средний выигрыш при смешанной стратегии , а второй применяет свою чистую стратегию Y.

 

2) — выигрыш, когда применяется чистая стратегия х первым игроком и смешанная стратегия вторым игроком.

 

3) Если применяется чистая стратегия х первого игрока и Y второго игрока, то выигрыш первого игрока определяется следующим выражением:

4) Если применяем стратегию смешанной стратегии первого и второго игрока:

— средний выигрыш первого игрока

 

при некоторых смешанных стратегиях и

Будем рассматривать случай когда функция выигрышей 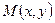была на единичном квадрате выпуклой или вогнутой.

Непрерывность и ее выпуклость (вогнутость) приводит к тому, что функция имеет единственной экстремум.

 

Теорема о непрерывных антагонистических играх на единичном квадрате при выпуклой (вогнутой) функции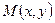

Пусть 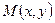непрерывная функция выигрышей первого игрока на единичном квадрате и строго выпукла или вогнута по х и у, тогда имеются единственные оптимальные чистые стратегии для первого и второго игроков:

 

и цена игры определяется функциями:

а чистые стратегии игроков определяются уравнениями:

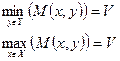
Пример: Пусть на единичном квадрате [0,1] задана функция

Если первый игрок применяет чистые стратегии от 0 до , то второй игрок должен применять свою чистую стратегию .

Если первый игрок применяет чистые стратегии в интервале 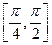, то второй должен применять чистую стратегию .