Признак. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

17. Признаки подобия треугольников.

Определение. Треугольники подобны, если их стороны пропорциональны, а углы равны.

Признак. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Признак. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

18. Свойства сторон треугольника.

Свойство: 1. Любая сторона меньше суммы двух других сторон и больше их разности.

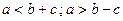
19. Определение перпендикуляра, проекции и наклонной.

Определение. Перпендикуляром, проведенным из некоторой точки до заданной прямой, называется отрезок, лежащий на прямой, перпендикулярной заданной прямой и с концами в заданной точке, и точке, лежащей на заданной прямой.

Определение. Наклонная -любой отрезок, проведенный из точки на прямую отличный от перпендикуляра.

Определение. Проекция наклонной на прямую- отрезок, соединяющий конец перпендикуляра и наклонной к прямой, проведенных из одной точки.

20. Сравнение длины перпендикуляра и наклонной.

Свойство: 1. Длина наклонной всегда больше перпендикуляра.

21. Свойство перпендикуляра, проведенного к отрезку через его середину.(серединный перпендикуляр).

Определение. Серединный перпендикуляр- это перпендикуляр проведенный к отрезку через его середину.

Свойство: 1. Серединные перпендикуляры пересекаются в одной точке ( центр описанной окружности)

Свойство: 2. В прямоугольном треугольнике серединные перпендикуляры пересекаются в середине гипотенузы.

22. Определение параллелограмма. Свойства диагоналей прямоугольника.

Определение. Параллелограмм- четырехугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых.

Свойство: 1. Противолежащие стороны параллелограмма попарно равны и параллельны.

Свойство: 2. Противолежащие углы параллелограмма попарно равны.

Свойство: 3. Диагонали в точке их пересечения делятся пополам.

Свойство: 4. Сумма «соседних» углов равна 180 градусов.

23. Признак параллелограмма.

Четырехугольник является параллелограммом, если:

Признак. Противолежащие стороны четырехугольника попарно равны.

Признак. Противолежащие углы четырехугольника попарно равны.

Признак. Диагонали четырехугольника делятся в точке их пересечения пополам.

Признак. Сумма «соседних» углов равна 180 градусов.

Признак. Противолежащие стороны четырехугольника параллельны.

 

24. Определение прямоугольника. Свойства диагоналей прямоугольника.

Определение. Прямоугольник- параллелограмм, у которого все углы прямые.

Свойство: 1. Длины диагоналей прямоугольника равны.

Свойство: 2. Диагонали прямоугольника делятся точкой пересечения пополам.

Свойство: 3. Диагональ прямоугольника вычисляется по теореме Пифагора.

25. Определение ромба. Свойства диагоналей ромба.

Определение. Ромб- параллелограмм, у которого все стороны равны.

Свойство: 1. Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.

Свойство: 2. Диагонали ромба являются биссектрисами его углов.

Свойство: 3. Сумма квадратов диагоналей равны квадрату стороны, умноженному на 4. .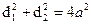

26. Определение квадрата. Свойства квадрата.

Определение. Квадрат - ромб с прямыми углами ( четырехугольник у которого все стороны и углы равны.)

Свойство: 1. Все углы квадрата прямые

Свойство: 2. Диагонали квадрата равны.

Свойство: 3. Диагонали квадрата взаимно перпендикулярны.

Свойство: 4. Диагонали квадрата делятся точкой пересечения пополам.

Свойство: 5. Диагонали квадрата являются биссектрисами его углов.

27. Определение трапеции. Определение и свойства средней линии трапеции.

Определение. Трапеция– четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.

Определение. Средняя линия трапеции- отрезок соединяющий середины боковых(не параллельных) сторон.

Свойство: 1. Средняя линия трапеции параллельна основаниям и равна их полусумме ().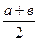

28. Определение окружности, хорды, диаметра, секущей, касательной.

Определение. Окружность – фигура которая состоит из всех точек плоскости равноудаленных от данной точки(центра окружности).

Определение. Хорда - отрезок соединяющий две точки на окружности.

Определение. Диаметр - хорда проходящая через центр окружности.

Определение. Секущая - это прямая, пересекающая окружность в двух точках.

Определение. Касательная - прямая, имеющая только одну точку пересечения с окружностью.

29. Через сколько точек можно провести окружность и только одну?

Свойство: 1.Через три точки, не лежащие на одной прямой, можно провести окружность и притом только одну.

30. Свойство диаметра перпендикулярного хорде.

Свойство: 1. Диаметр перпендикулярный хорде делит эту хорду пополам.

31. Свойство дуг, заключенных между параллельными хордами.

Свойство: 1. Дуги, заключенные между параллельными хордами, равны.

32. Зависимость между дугами, хордами и расстояниями хорд от центра.

В одном круге или в равных кругах:

Свойство: 1. Если дуги равны, то стягивающие их хорды равны и одинаково удалены от центра.

Свойство: 2. Если две дуги, меньшие полуокружности, не равны , то большая из них стягивается большей хордой и из обеих хорд большая расположена ближе к центру.

33. Свойства касательной.

Определение. Касательная - прямая, имеющая только одну точку пересечения с окружностью.

Свойство: 1. Касательная к окружности перпендикулярна к радиусу проведенного в точку касания.

Свойство: 2. Две касательные проведенные из одной точки к окружности - равны.

34. Случаи взаимного расположения окружностей.

 

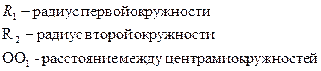
1. Окружности не пересекаются( окружности лежат вне другой)

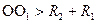
2. Окружности имеет внешнее касание

3. Окружности имеет внутренне касание

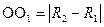
4. Окружности пересекаются

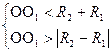
5. Одна окружность лежит внутри другой

 

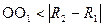
35. Определение вписанного угла, центрального угла. Измерение их величин. Свойство вписанного угла, его связь с центральным углом, опирающимся на туже хорду.

 

Определение. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность - вписанный угол.

Определение. Центральный угол в окружности - плоский угол с вершиной в ее центре.

 

Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Свойство: 1. Все вписанные углы, опираются на одну и ту же дугу, равны между собой.

Свойство: 2. Вписанный угол, опирающийся на диаметр прямой.

36. Угол с вершиной внутри круга; угол с вершиной вне круга; угол межу касательной и хордой. Измерение их величин.

 

Свойство: 1. Угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, из которых одна заключается между его сторонами, а другая между продолжениями сторон.

Свойство: 2. Угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами.

Свойство: 3. Угол, составленный касательной и хордой, измеряется половиной дуги заключенной внутри него.

37. Свойство хорд, пересекающихся в круге.

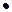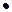Свойство: 1. Если хорды, АВ и СD окружности пересекаются в точке S, то ASВS=DSCS.

38. Свойство секущей и касательной, проведенной из одной точки.

Свойство: 1. Произведение отрезков секущей окружности равно квадрату отрезка касательной, проведенной из той же точки.

39. Свойство секущих, проведенных из одной точки.

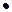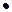Если из одной точки P к окружности проведены две секущие, пересекающие окружность в точках A,B,C,D соответственно, то APВP=CPDP.

40. Четыре замечательные точки окружности.

1. Точка пересечения медиан – центр тяжести треугольника.

2. Точка пересечения высот – ортоцентр треугольника.

3. Точка пересечения биссектрис – центр вписанной окружности.

4. Точка пересечения серединных перпендикуляров – центр описанной окружности.

Во всяком треугольнике точка пересечения медиан, точка пересечения высот (или их продолжений) и точка пересечения серединных перпендикуляров к сторонам треугольника лежат на одной прямой (эта прямая называется прямой Эйлера).

41. Свойство высот треугольника.

Определение. Высота треугольника- это перпендикуляр, опущенный из любой вершины на противоположную сторону или ее продолжение.

Свойство: 1. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.

Свойство: 2. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Свойство: 3. Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон

Свойство: 4. Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

42. Свойства вписанного и описанного четырехугольника.

Свойство: 1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равна 180 градусов.

Свойство: 2. Четырехугольник можно описать около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

43. Свойства прямоугольного треугольника

Теорема Пифагора. В любом прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

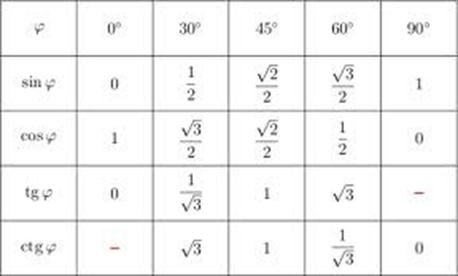
синус угла х - это отношение противолежащего катета к гипотенузе.

косинус угла х - это отношение прилежащего катета к гипотенузе.

тангенс угла х - это отношение противолежащего катета к прилежащему.

котангенс угла х - это отношение прилежащего катета к противолежащему.

Развернуть

Открыть в широком формате