Определение показательной, логарифмической и степенной функций
Определение показательной, логарифмической и степенной функций.
Показательная функция.
Функция 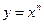 непрерывна и строго монотонна на
непрерывна и строго монотонна на 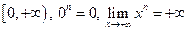 , поэтому у нее существует непрерывная обратная, тоже определенная на всей полуоси
, поэтому у нее существует непрерывная обратная, тоже определенная на всей полуоси 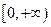 . То есть для любого положительного действительного числа
. То есть для любого положительного действительного числа 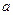 и произвольного натурального
и произвольного натурального  найдется единственное число
найдется единственное число 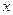 (корень
(корень 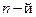 степени из
степени из 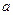 ) такое, что
) такое, что  , его обозначают
, его обозначают 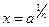 . Определим показательную функцию для рациональных значений аргумента по формуле
. Определим показательную функцию для рациональных значений аргумента по формуле  .
.
Функция  будет монотонной на
будет монотонной на 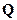 , а именно, монотонно возрастающей при
, а именно, монотонно возрастающей при 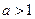 и, соответственно, убывающей при
и, соответственно, убывающей при 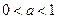 . Поэтому, так как
. Поэтому, так как
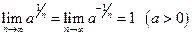 ,
,
то  , если
, если  . Из последнего соотношения вытекает свойство, которое мы назовем непрерывностью показательной функции на множестве рациональных чисел.
. Из последнего соотношения вытекает свойство, которое мы назовем непрерывностью показательной функции на множестве рациональных чисел.
Утверждение. Если последовательности рациональных чисел  и
и  ограничены и
ограничены и  , то
, то  .
.
Рассмотрим теперь произвольное действительное число 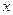 . Обозначим через
. Обозначим через  множество рациональных точек, лежащих левее точки
множество рациональных точек, лежащих левее точки 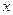 , а через
, а через 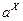 множество значений показательной функции в точках множества
множество значений показательной функции в точках множества  :
:
 .
.
Через  обозначим множество рациональных точек, лежащих правее точки
обозначим множество рациональных точек, лежащих правее точки 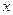 и, соответственно через
и, соответственно через  множество значений показательной функции в этих точках.
множество значений показательной функции в этих точках.
 .
.
Из монотонности показательной функции на множестве рациональных чисел следует, что множество 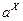 лежит левее множества
лежит левее множества  , поэтому в силу аксиомы непрерывности существует такое число, которое мы обозначим через
, поэтому в силу аксиомы непрерывности существует такое число, которое мы обозначим через  , что
, что  для всех
для всех 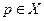 и
и  .
.
Поскольку расстояние между точками множеств  и
и  может быть сколь угодно малым, то из непрерывности показательной функции на множестве рациональных чисел следует, что точки множеств
может быть сколь угодно малым, то из непрерывности показательной функции на множестве рациональных чисел следует, что точки множеств 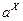 и
и  тоже могут лежать сколь угодно близко. Поэтому число
тоже могут лежать сколь угодно близко. Поэтому число  - единственное.
- единственное.
Определение. Отображение 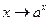 называется показательной или экспоненциальной функцией при основании
называется показательной или экспоненциальной функцией при основании 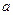 .
.
Монотонность и непрерывность показательной функции на 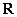 вытекает из монотонности и непрерывности ее на множестве
вытекает из монотонности и непрерывности ее на множестве 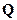 .
.
Функция  обладает следующими свойствами
обладает следующими свойствами
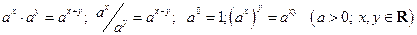 .
.
Замечание. Из непрерывности показательной функции и того, что
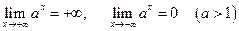 ,
,
 ,
,
следует, что множество значений функции  - полуось
- полуось 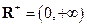 .
.