Несобственные интегралы
Несобственные интегралы.
Несобственные интегралы первого рода.
, (1) если этот предел существует, называется несобственным интегралом от функции по… Говорят, что интеграл сходится, если конечный предел существует и расходится в противном случае.Утверждение. Если функция определена в промежутке и интегрируема на любом отрезке , содержащемся в этом промежутке, то интегралы и сходятся и расходятся одновременно.
Задача. Докажите это утверждение.
Пример 1. Выясним, при каких значениях параметра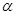 
сходится интеграл 
.
.
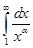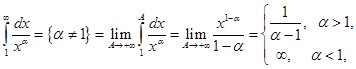
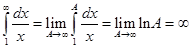Из определения несобственного интеграла видно, что сходимость интеграла равносильна существованию предела функции 
при 
.
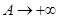Утверждение(критерий Коши сходимости несобственного интеграла). Если функция
определена на промежутке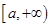 
и интегрируема на любом отрезке 
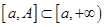, то интеграл 
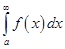сходится тогда и только тогда, когда для любого 
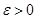можно указать такое 
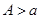, что для любых 
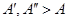имеет место соотношение
.
Доказательство.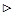 
В самом деле,
,
поэтому сформулированное условие есть критерий Коши существования предела функци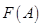и 
при .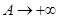
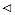
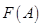Утверждение. Если функция неотрицательна, то интеграл представляет собой неубывающую функцию, и для сходимости интеграла (1) необходимо и достаточно ограниченности функции на .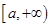
Справедливость этого утверждения следует из определения несобственного интеграла и теоремы о пределе монотонной функции.
Признаки сравнения сходимости несобственных интегралов.
Доказательство. Из условия теоремы и соответствующих неравенств для определенного интеграла Римана при любом имеем . Из ограниченности функции на следует ограниченность а, значит, и сходимость . Сходимость интеграла следует из…Абсолютная сходимость несобственных интегралов.
Утверждение. Если интегралсходится абсолютно, то он сходится. Доказательство. Достаточно проверить признак Коши для сходимости интеграла : … .Несобственные интегралы второго рода.
, (2) если этот предел существует, называется несобственным интегралом от функции по… Говорят, что интеграл сходится, если конечный предел существует и расходится в противном случае.Утверждение. Если функция определена в промежутке , интегрируема на любом отрезке , содержащемся в этом промежутке и неограниченна в любой полуокрестности , то интегралы и сходятся и расходятся одновременно.
Задача. Докажите это утверждение.
Пример 2. Выясним, при каких значениях параметра 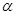сходится интеграл 
.
.
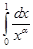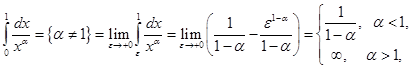
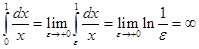Признаки сравнения сходимости несобственных интегралов второго рода.
Пусть функции и определены на промежутке , и пусть для некоторого на промежутке справедливо неравенство . Тогда из сходимости интеграла вытекает сходимость интеграла , а из… Теорема (предельный признак сравнения). Пусть положительные функции и определены на промежутке , и пусть существует…Абсолютная сходимость несобственных интегралов.
Определение. Говорят, что несобственный интеграл 
сходится абсолютно, если сходится интеграл 
.
Утверждение. Если интегралсходится абсолютно, то он сходится.