Подстановка в определенных интегралах
Лекция 40. Вычисление определенного интеграла. Замена переменной в определенном интеграле. Интегрирование по частям. Некоторые приложения определенных интегралов. Понятие о несобственных интегралах.
Подстановка в определенных интегралах.
Пусть y = f(x) – непрерывная на промежутке [a; b] оси ox функция, а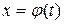 
- непрерывная на промежутке [α; β] функция, имеющая к тому же на [α;β] непрерывную производную (то есть x=φ(t) – непрерывно дифференцируемая на [α; β] функция). Кроме того, будем считать, что когда переменная t меняется от α до β, то переменная x = φ(t) меняется от a до b. Таким образом, φ(α) = b и φ(β) = b. Тогда при вычислении 
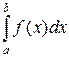можно совершить подстановку по следующей схеме:
|
(1)
Докажем правомочность схемы (1). Пусть
| (2) |
Здесь F(x) – некоторая первообразная для функции f(x). То есть F΄(x) = f(x). Но тогда, по правилу вычисления производной сложной функции,
| (3) |
Поэтому по формуле Ньютона-Лейбница
| (4) |
Равенство результатов (2) и (4) и доказывает правомочность схемы (1).
Кстати, сравнивая схему (1) вычисления определенных интегралов с помощью подстановки с аналогичной схемой вычисления неопределенных интегралов, можно увидеть и то, что в этих схемах общее, и то, что различно.
Примечание. На практике часто бывает удобнее делать подстановку не вида x = φ(t), а вида t = φ(x).
Вычисление определенных интегралов по частям.
Мы уже знаем, что по частям можно вычислять неопределенные интегралы. Для этого используется уже полученная формула 
. Но по частям можно вычислять и определенные интегралы. Это делается по внешне похожей формуле (5):
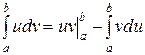
| (5) |
Здесь 
и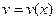 
– любые две непрерывные на [a; b] функции, имеющие на этом промежутке и непрерывные производные 
и 
(то есть и 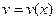- непрерывно дифференцируемые на [a; b] функции).
Докажем формулу (5). Учтем, что
| (6) |
Функция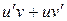 
, стоящая в этом равенстве справа, согласно указанных выше условий для функций 
и 
, является непрерывной на промежутке [a; b]. Значит, существует определенный интеграл от нее:
| (7) |
С другой стороны, согласно (6), функция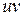 
является первообразной для функции 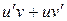. А значит, по формуле Ньютона-Лейбница получаем:
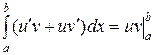
| (8) |
Сравнивая (7) и (8), приходим к доказываемой формуле (5).
Пример 1. Вычислить 
.
Решение:
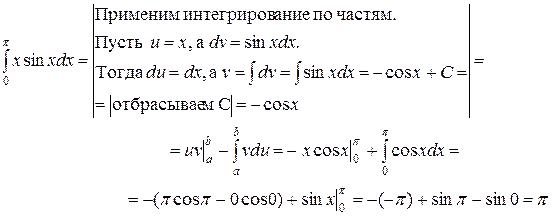
Использование четности-нечетности подынтегральной функции при вычислении определенных интегралов с симметричными пределами интегрирования.
б) Если f(x) – непрерывная и нечетная на промежутке [-a; a] функция, то (10) Доказательство. Рассмотрим рисунки 1(а) и 1(б), соответствующие случаям (а) и…Упражнения
а) б) в) Ответы: а) 1 – ln2; б) ; в) . 2. Вычислить интегрированием по частям:Несобственные интегралы