рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Несобственные интегралы с бесконечными пределами интегрирования.
Реферат Курсовая Конспект
Несобственные интегралы с бесконечными пределами интегрирования.
Несобственные интегралы с бесконечными пределами интегрирования. - раздел Математика, Подстановка в определенных интегралах Пусть Y = F(X) – Заданная И Непрерывная Для Всех X ≥ α...
Пусть y = f(x) – заданная и непрерывная для всех x ≥ α функция. Тогда для любого b ≥ a существует 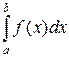 . Поставим вопрос о пределе этого интеграла при b → ¥.
. Поставим вопрос о пределе этого интеграла при b → ¥.
Определение.

| (11) |
называется несобственным интегралом от функции f(x) с бесконечным верхним пределом. Если этот предел существует и конечен, то несобственный интеграл  называется сходящимся. А если же он не существует или равен
называется сходящимся. А если же он не существует или равен
± ¥, то этот несобственный интеграл называется расходящимся.
Если f(x) ≥ 0 для всех x ≥ a, то у несобственного интеграла (11) имеется очевидный геометрический смысл, вытекающий из геометрического смысла обычного определенного интеграла. Действительно, согласно рис. 2. 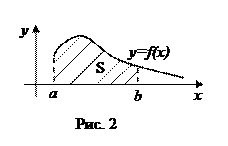
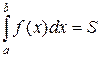 (12)
(12)
А тогда

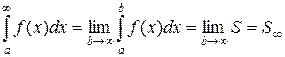 (13)
(13)
Здесь S¥ - площадь бесконечно протяженной в направлении оси ох криволинейной трапеции (рис.3). Несмотря на свою бесконечную протяженность, она может оказаться и конечной. Но это может произойти, согласно рис. 3, лишь в случае, когда y =f(x) → 0 при x →¥. Да и то, если функция y =f(x) → 0 при x → ¥ достаточно быстро.
Пример 3. Найти площадь S¥, изображенную на рис. 4.

Решение:
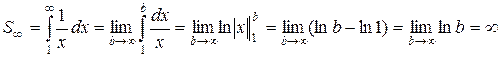 ,
,
так как lnb → ¥ при b → ¥.
Итак, S¥ = ¥. И это несмотря на то, что функция 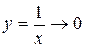 при x → ¥. Несобственный интеграл
при x → ¥. Несобственный интеграл  , а значит, он расходится.
, а значит, он расходится.
Пример 4. Найти площадь S¥ , изображенную на рис. 5.
Решение:
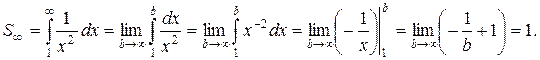
Здесь S¥ = 1. То есть бесконечно протяженная площадь оказалась конечной. Это произошло потому, что подынтегральная функция  при x → ¥ достаточно быстро (по крайней мере, гораздо быстрее, чем подынтегральная функция
при x → ¥ достаточно быстро (по крайней мере, гораздо быстрее, чем подынтегральная функция  в предыдущем примере). Несобственный интеграл
в предыдущем примере). Несобственный интеграл 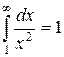 (число), а значит, он сходится.
(число), а значит, он сходится.
Пример 5. Выяснить, сходится или расходится несобственный интеграл 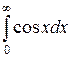 .
.
Решение. Вычислим это интеграл:

– не существует. Это очевидно, если вспомнить поведение графика функции y= = sinx (синусоиды) при x → ¥. Таким образом, 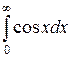 не существует, а значит, он расходится. Впрочем, это и не могло быть иначе, ибо подынтегральная функция cosx не стремится к нулю при х → ¥.
не существует, а значит, он расходится. Впрочем, это и не могло быть иначе, ибо подынтегральная функция cosx не стремится к нулю при х → ¥.
Заметим, что при вычислении несобственных интегралов типа  , как и при вычислении обычных определенных интегралов
, как и при вычислении обычных определенных интегралов 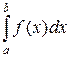 , можно сразу применять формулу Ньютона-Лейбница:
, можно сразу применять формулу Ньютона-Лейбница:
 Здесь Здесь 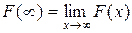
| (14) |
Действительно:

Если значение F(¥) существует и конечно, то согласно формуле (14) Ньютона-Лейбница сходится и несобственный интеграл  .
.
Примечание. Совершенно аналогично интегралам с бесконечным верхним пределом можно рассматривать несобственные интегралы с бесконечным нижним пределом и даже с обоими бесконечными пределами интегрирования. То есть интегралы вида
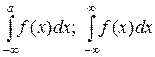
| (15) |
Для их вычисления тоже можно применять формулу Ньютона-Лейбница.
Пример 6.
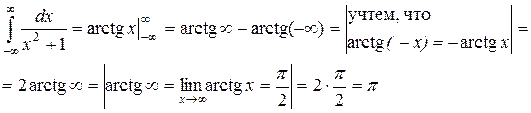
Итак,  (число), то есть этот интеграл сходится. Его величина π равна площади S¥ бесконечно протяженной в обе стороны фигуры, изображенной на рис. 6.
(число), то есть этот интеграл сходится. Его величина π равна площади S¥ бесконечно протяженной в обе стороны фигуры, изображенной на рис. 6. 
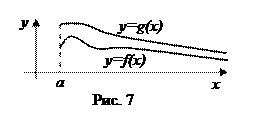 Заметим, что сам факт сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования не обязательно устанавливать с помощью прямого вычисления этих интегралов. Это вопрос часто можно решить и гораздо проще, сравнив данный несобственный интеграл с каким-либо другим, для которого сходимость-расходимость уже установлена.
Заметим, что сам факт сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования не обязательно устанавливать с помощью прямого вычисления этих интегралов. Это вопрос часто можно решить и гораздо проще, сравнив данный несобственный интеграл с каким-либо другим, для которого сходимость-расходимость уже установлена.
Пусть, например, для всех 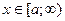 имеет место неравенство f(x)£ g(x), где y = f(x) и y = g(x) – две непрерывные и неотрицательные функции (рис.7). Тогда очевидно, что
имеет место неравенство f(x)£ g(x), где y = f(x) и y = g(x) – две непрерывные и неотрицательные функции (рис.7). Тогда очевидно, что
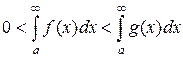
| (16) |
Из неравенства (6) и рис. 7 очевидным образом следует так называемый признак сравнения несобственных интегралов:
1) Если 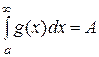 (число) - сходится, то и (число) - сходится, то и 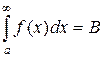 (число) - сходится, причем B<A.
2) Если (число) - сходится, причем B<A.
2) Если  - расходится, то и - расходится, то и 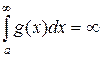 - расходится.
3) Если - расходится.
3) Если 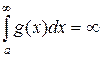 - расходится, то - расходится, то  - об этом интеграле ничего сказать нельзя.
4) Если - об этом интеграле ничего сказать нельзя.
4) Если 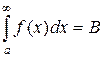 (число) - сходится, то (число) - сходится, то  - об этом интеграле ничего сказать нельзя. - об этом интеграле ничего сказать нельзя.
| (17) |
В качестве функции g(x), с которой на промежутке  сравнивают данную функцию f(x), часто используют функцию
сравнивают данную функцию f(x), часто используют функцию  , а в качестве интеграла сравнения – интеграл
, а в качестве интеграла сравнения – интеграл 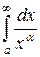 , учитывая при этом, что при a > 0 и любых α функция
, учитывая при этом, что при a > 0 и любых α функция  - положительная и непрерывная функция, и что
- положительная и непрерывная функция, и что
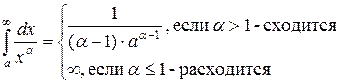
| (18) |
Пример 7. Исследовать на сходимость-расходимость 
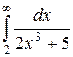
Решение. Очевидно, что 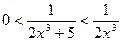 для всех x Î [2; ¥). Поэтому
для всех x Î [2; ¥). Поэтому
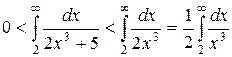 .
.
Но согласно (18) интеграл  сходится. Поэтому, по признаку сравнения, сходится и
сходится. Поэтому, по признаку сравнения, сходится и 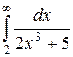 (он представляет собой некоторой конкретное число). Более того, предыдущее неравенство дает и оценку этого числа: так как, согласно (18),
(он представляет собой некоторой конкретное число). Более того, предыдущее неравенство дает и оценку этого числа: так как, согласно (18),  , то
, то
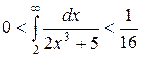 .
.
Пример 8. Исследовать на сходимость-расходимость 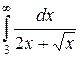 .
.
Решение. Очевидно, что
 для всех x Î [3; ¥).
для всех x Î [3; ¥).
Следовательно,
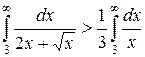 .
.
Но последний интеграл равен ¥. Следовательно, равен ¥ и 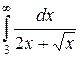 . То есть он расходится.
. То есть он расходится.
Примечание. Справедлив и более сильный (обобщенный) признак сравнения, который применим для любых непрерывных и неотрицательных на
[a; ¥) функций. А именно, если
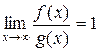 , ,
| (19) |
то есть если f(x) эквивалентна g(x) (f(x) ~ g(x)) при х ® ¥, то несобственные интегралы
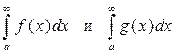
сходятся или расходятся одновременно.
Пример 9. Исследовать на сходимость-расходимость  .
.
Решение. Исследовав функцию  , легко показать, что она определена, а следовательно и непрерывна для всех х Î [10; ¥). При этом
, легко показать, что она определена, а следовательно и непрерывна для всех х Î [10; ¥). При этом

Но, согласно (18), 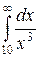 сходится. Поэтому и
сходится. Поэтому и  сходится.
сходится.
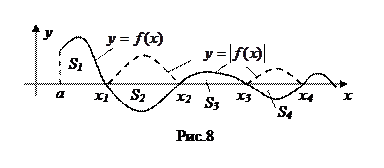 Теперь перейдем к более сложному случаю несобственных интегралов с бесконечными пределами интегрирования, когда подынтегральная функция знакопеременна на своей области интегрирования (рис.8). Тогда
Теперь перейдем к более сложному случаю несобственных интегралов с бесконечными пределами интегрирования, когда подынтегральная функция знакопеременна на своей области интегрирования (рис.8). Тогда
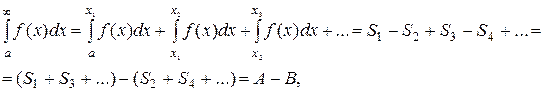
| (20) |
где А>0 – сумма площадей, находящихся над осью ох, а В>0 – сумма площадей, находящихся под осью ох.
Рассмотрим еще один несобственный интеграл, только уже от |f(x)|:
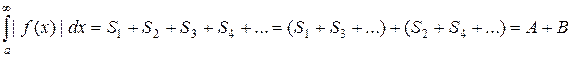
| (21) |
а) Допустим, что 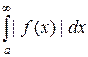 сходится. Тогда А + В – конечное положительное число. А значит, и его положительные слагаемые А и В – конечные положительные числа. Но тогда и их разность А – В – конечное число (его знак может быть любым). А значит, согласно (20), несобственный интеграл
сходится. Тогда А + В – конечное положительное число. А значит, и его положительные слагаемые А и В – конечные положительные числа. Но тогда и их разность А – В – конечное число (его знак может быть любым). А значит, согласно (20), несобственный интеграл  сходится.
сходится.
б) Допустим, что 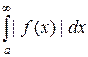 расходится (равен +¥). Тогда сумма А+В = +¥, а значит, или А, или В, или оба они одновременно равны +¥. Но их разность А – В может оказаться как бесконечной, так и конечной. То есть
расходится (равен +¥). Тогда сумма А+В = +¥, а значит, или А, или В, или оба они одновременно равны +¥. Но их разность А – В может оказаться как бесконечной, так и конечной. То есть  может как сходиться, так и расходиться.
может как сходиться, так и расходиться.
Если  сходится, и при этом
сходится, и при этом 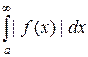 сходится, то говорят, что
сходится, то говорят, что  сходится абсолютно. Величину абсолютно сходящегося несобственного интеграла
сходится абсолютно. Величину абсолютно сходящегося несобственного интеграла  можно и оценить:
можно и оценить:
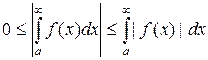
| (22) |
Действительно, неравенство (22) равносильно очевидному неравенству
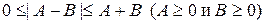
| (23) |
А если  сходится, но при этом
сходится, но при этом 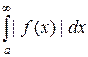 расходится, то говорят, что
расходится, то говорят, что  сходится условно.
сходится условно.
Пример 10. Показать, что  сходится, причем абсолютно.
сходится, причем абсолютно.
Решение. Рассматривая  и используя признак сравнения (17), получаем:
и используя признак сравнения (17), получаем:
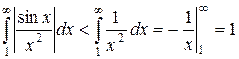
Таким образом,  сходится. Но тогда и
сходится. Но тогда и  сходится, причем абсолютно. Более того, мы можем произвести, используя неравенство (22), оценку этого интеграла:
сходится, причем абсолютно. Более того, мы можем произвести, используя неравенство (22), оценку этого интеграла:

То есть абсолютная величина интеграла  заключена в пределах
заключена в пределах
[0; 1].
Пример 11. Доказать, что 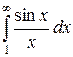 сходится, но условно.
сходится, но условно.
Решение. Применим к этому интегралу формулу (5) интегрирования по частям:

Интеграл  , как и рассмотренный в примере 10 интеграл
, как и рассмотренный в примере 10 интеграл  , сходится. А значит, сходится и
, сходится. А значит, сходится и 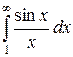 . Но сходится он условно, ибо
. Но сходится он условно, ибо 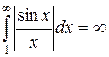 (расходится).
(расходится).
Действительно, так как  для всех х, то
для всех х, то 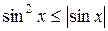 для всех х. А значит
для всех х. А значит
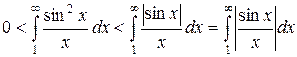
Но
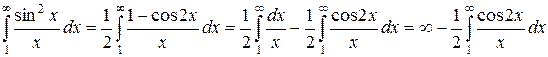
Последний интеграл 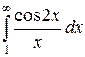 , как и аналогичные интегралы
, как и аналогичные интегралы 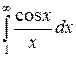 и
и 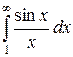 , сходится (это можно подтвердить интегрированием по частям). То есть
, сходится (это можно подтвердить интегрированием по частям). То есть 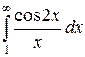 - число. А значит,
- число. А значит,  (расходится). Но тогда и бóльший интеграл
(расходится). Но тогда и бóльший интеграл 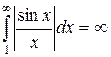 (расходится). То есть
(расходится). То есть 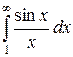 сходится, но условно.
сходится, но условно.
Несобственные интегралы с конечными пределами интегрирования
от неограниченных функций.
Под указанными несобственными интегралами понимаются интегралы вида 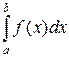 , где f(x) – разрывная в некоторой точке (точках) конечного промежутка интегрирования [a; b] функция, обращающаяся в этих точках в бесконечность (любого знака).
, где f(x) – разрывная в некоторой точке (точках) конечного промежутка интегрирования [a; b] функция, обращающаяся в этих точках в бесконечность (любого знака).
Будем пока считать, что такая точка одна, и эта точка – правая крайняя точка промежутка интегрирования (верхний предел b интеграла 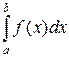 ). То есть будем считать, что функция f(x) непрерывна на полуинтервале [a; b), причем
). То есть будем считать, что функция f(x) непрерывна на полуинтервале [a; b), причем
| f(x) ® ±¥ при х ® b | (24) |
Под интегралом 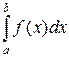 в этом случае, по определению, понимается предел обычного определенного интеграла
в этом случае, по определению, понимается предел обычного определенного интеграла 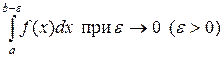 :
:

| (25) |
Этот интеграл 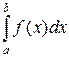 называется несобственным интегралом от функции, неограниченной на правом конце промежутка интегрирования. Если он существует и конечен, то он называется сходящимся. Если же не существует или равен +¥ или -¥, то он называется расходящимся.
называется несобственным интегралом от функции, неограниченной на правом конце промежутка интегрирования. Если он существует и конечен, то он называется сходящимся. Если же не существует или равен +¥ или -¥, то он называется расходящимся.
В частности, если f(x)≥0 на [a; b) и f(x) ® +¥ при х ® b, то геометрическую иллюстрацию равенства (25) дают рисунки 5.21(а) и 5.21(б):
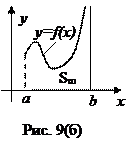

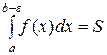
 (26)
(26)
Таким образом, согласно рис. 9(б),  - площадь бесконечно протяженной вдоль оси оу криволинейной трапеции. А она, как и площадь S¥ на рис.3, может оказаться как конечной, так и бесконечной. То есть несобственный интеграл
- площадь бесконечно протяженной вдоль оси оу криволинейной трапеции. А она, как и площадь S¥ на рис.3, может оказаться как конечной, так и бесконечной. То есть несобственный интеграл 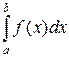 может оказаться как сходящимся, так и расходящимся.
может оказаться как сходящимся, так и расходящимся.
Установить сходимость или расходимость несобственного интеграла 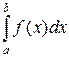 можно на основе его прямого вычисления по формуле Ньютона-Лейбница:
можно на основе его прямого вычисления по формуле Ньютона-Лейбница:

| (27) |
Подтвердим это, исходя из определения (25):

Пример 12. Вычислить несобственный интеграл 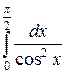 .
.
Решение. Этот интеграл действительно несобственный, так как его подынтегральная функция 
 имеет особую точку
имеет особую точку 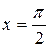 , в которой
, в которой 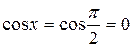 , а значит, в которой функция
, а значит, в которой функция  обращается в бесконечность:
обращается в бесконечность:
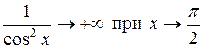
Вычисляя указанный интеграл по формуле Ньютона-Лейбница (27), получим:
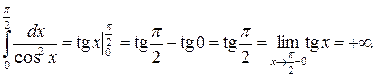
Таким образом, данный несобственный интеграл расходится.
Примечание. Мы ввели понятие несобственного интеграла 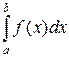 от функции f(x), неограниченной (обращающейся в бесконечность) на правом конце промежутка интегрирования [a; b]. Но этот же интеграл будет несобственным, если f(x) неограничена на левом конце промежутка интегрирования (в точке а), а также в некоторой внутренней его точке с. В последнем случае
от функции f(x), неограниченной (обращающейся в бесконечность) на правом конце промежутка интегрирования [a; b]. Но этот же интеграл будет несобственным, если f(x) неограничена на левом конце промежутка интегрирования (в точке а), а также в некоторой внутренней его точке с. В последнем случае 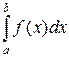 разбивают на два несобственных интеграла:
разбивают на два несобственных интеграла:
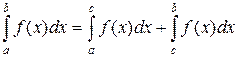
| (28) |
Оба эти интеграла с особой точкой на краю промежутка интегрирования можно вычислять по формуле Ньютона-Лейбница.
Пример 13. Вычислив несобственный интеграл  , доказать сходимость этого интеграла. Полученному результату дать геометрическую иллюстрацию.
, доказать сходимость этого интеграла. Полученному результату дать геометрическую иллюстрацию.
Решение. Данный интеграл действительно несобственный, так как его подынтегральная функция  обращается в ¥ в точке х = 0 (
обращается в ¥ в точке х = 0 (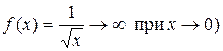 . Вычислим его по формуле Ньютона-Лейбница:
. Вычислим его по формуле Ньютона-Лейбница:

Таким образом  сходится. Его геометрическая иллюстрация дана на рис. 10.
сходится. Его геометрическая иллюстрация дана на рис. 10.
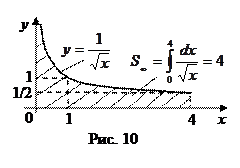 Заметим, что вопрос о сходимости-расходимости несобственных интегралов от неограниченных функций, как и вопрос о сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования, совсем не обязательно выяснять, вычисляя эти интегралы. Можно попробовать сравнить данный несобственный интеграл с каким-либо другим с теми же пределами интегрирования.
Заметим, что вопрос о сходимости-расходимости несобственных интегралов от неограниченных функций, как и вопрос о сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования, совсем не обязательно выяснять, вычисляя эти интегралы. Можно попробовать сравнить данный несобственный интеграл с каким-либо другим с теми же пределами интегрирования.
 Пусть, например, y = f(x) и y = g(x) – две непрерывные в полуинтервале
Пусть, например, y = f(x) и y = g(x) – две непрерывные в полуинтервале
[a; b) и неотрицательные функции. И пусть f(x) £ g(x) для всех х Î [a; b). Пусть, кроме того, f(x) ® +¥ и g(x) ® +¥ при х ® b (рис. 11). Тогда, очевидно,
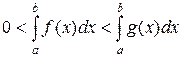
| (29) |
Из этого неравенства очевидным образом вытекает следующий признак сравнения:
а) Если 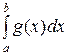 = (число)– сходится, то и = (число)– сходится, то и 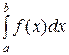 =(число)– сходится.
б) Если =(число)– сходится.
б) Если  – расходится, то и – расходится, то и 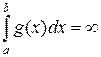 – расходится – расходится
| (30) |
В качестве функции g(x), с которой сравнивают данную функцию f(x), часто используют функцию 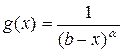 , учитывая при этом, что
, учитывая при этом, что
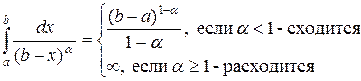
| (31) |
Пример 14. Исследовать на сходимость-расходимость 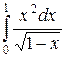 .
.
Решение. Подынтегральная функция 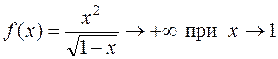 , поэтому данный интеграл является несобственным. При этом очевидно, что для всех х Î [0; 1)
, поэтому данный интеграл является несобственным. При этом очевидно, что для всех х Î [0; 1)
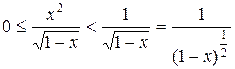
Но 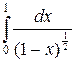 , согласно (31), сходится. Поэтому и меньший интеграл
, согласно (31), сходится. Поэтому и меньший интеграл 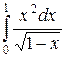 сходится. Более того, можем оценить и значение этого интеграла:
сходится. Более того, можем оценить и значение этого интеграла:
 .
.
Впрочем, мы можем вычислить этот интеграл и точно:
|

– Конец работы –
Эта тема принадлежит разделу:
Подстановка в определенных интегралах
Подстановка в определенных интегралах... Пусть y f x непрерывная на промежутке a b оси ox функция а...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Несобственные интегралы с бесконечными пределами интегрирования.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов