ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
Конспект лекций по дисциплине
«ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ»
Литература
1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. – 304 с.
2. Кирсанов М.Н. Графы в Maple. Задачи, алгоритмы, программы. – М.: ФИЗМАТЛИТ, 2007. – 168 с.
3. Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. – СПб.: Издательство «Лань», 2004. – 960 с. (глава V. Дискретная математика).
4. Фудзисава Т., Касами Т. Математика для радиоинженеров: Теория дискретных структур: Пер. с япон. – М.: Радио и связь, 1984. – 240 с.
5. Lovasz L., Vesztergombi K. Discrete Mathematics. – Yale: by Yale University Publishing, 1999. – 139 p.
6. Яблонский С. В. Введение в дискретную математику. – М.: Наука, 1986.
7. Мендельсон Э. Введение в математическую логику. М.: Наука, 1984.
8. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по курсу дискретной математики – М.: Наука. – 1992.
9. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.
10. Нефедов В. Н., Осипова В. А. Курс дискретной математики. – М.: Издательство МАИ, 1992.
11. Булос Дж., Джеффри Р. Вычислимость и логика. М.: Мир, 1994.
12. Курант Р., Роббинс Г. Что такое математика? –М.: МЦНМО, 2007. – 568 с.
Лекция № 1. ДИСКРЕТНОЕ И НЕПРЕРЫВНОЕ
Введение
Дискретная математика – это математика, не связанная с понятиями бесконечности, предела и непрерывности. Термин «дискретная математика» эквивалентен термину «конечная математика». Дискретная математика имеет широкий спектр приложений, прежде всего в областях, связанных с информационными технологиями и компьютерами. Когда говорят «цифровая вычислительная машина», то слово «цифровая» указывает на принципиально дискретный характер работы данного устройства.
Хотя различие между дискретным и непрерывным интуитивно понятно, все-таки оно достаточно тонко. Чтобы правильно понять его смысл и избежать недоразумений, необходимо ознакомиться с основами теории множеств.
Счетные и несчетные числовые множества
Среди других множеств особое положение занимают так называемые числовые множества. Первое числовое множество, которое открылось человеческому… Но даже простые натуральные числа имели какую-то тайну. Это множество имело… Существуют счетные и несчетные числовые множества. Очевидно, что множество, составленное из конечного числа…Лекция № 2. СИСТЕМЫ СЧИСЛЕНИЯ
Позиционные и непозиционные системы
Позиционная система счисления – система записи чисел в виде последовательности символов, в которой численное значение каждого символа зависит от его… Примером позиционной системы является хорошо известная десятичная система… Изобретение позиционной системы приписывается шумерам и вавилонянам. Затем она была развита индусами. В средневековой…Десятичная система
Десятичная система использует десять различных знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – которые обозначают натуральные числа в порядке их возрастания… Например, запись 483,56 в десятичной системе означает, что данное число… . (2.1)Двоичная система
Таблица 2.1 Десятичное число Бинарный код Код Грея Десятичное число … Предположим, что нам нужно преобразовать двоичное число с дробной частью 1100,1011 в более привычное десятичное число.…Код Грея
0110 0111 1000 1001. Числа 6 и 7, а также 8 и 9 отличаются друг от друга на один бит. Однако числа… Код Грея – система нумерации, в которой два соседних значения различаются только в одном разряде.Троичная система счисления
Таблица 2.3 Десятичная -3 -2 -1 … Элементы троичной системы существовали еще у древних шумеров. Полноценную симметричную троичную систему впервые…Восьмеричная и шестнадцатеричная системы счисления
В табл. 2.4 представлено 24-битное двоичное слово и соответствующие ему 8-ричный и 16-ричный коды. Таблица 2.4 Двоичный код Восьмеричный код …Лекция № 3. ФРАКТАЛЫ
Канторово множество
Рис. 3.1. Троичное канторово множествоElse
b(i)=1;
End
Sum=Sum+b(i)/(3^i);
End
x(k)=2*Sum;
y(k)=k/1024;
End
Plot(x, y)
Ковер Серпинского и снежинка Коха
Стохастические фракталы
В 1977 году в свет вышла книга американского математика Бенойта Мандельброта (1924-2010) «Фрактальная геометрия природы», в которой этот ученый… Графики случайных процессов, которые можно наблюдать на дисплеях приборов или… , (3.1)Энтропийная размерность
Пример 3.1. Например, если X – это отрезок [0, 1] с обычной метрикой, то значение приближенно равно 1/(2r), потому что необходимо 1/(2r) шаров (т.е.… Пример 3.2. Возьмем единичный квадрат . Тогда значение имеет порядок , потому… Определение. Если X – вполне ограниченное метрическое пространство, тогда число называется энтропийной размерностью…Фрактал Мандельброта
, (3.2) при начальном условии , не уходит в бесконечность.Лекция № 4. ОСНОВЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Виды доказательства
Рассмотрим классический пример. Задана так называемая большая посылка (или общее утверждение): «Все люди смертны». Также задана малая посылка… Если из малой посылки и заключения получают большую посылку, то такой метод… Таким образом, дедукция обладает неоспоримым преимуществом перед индукцией. Однако научное знание, как правило,…Логические высказывания, связки и операции
Высказывание – имеющее смысл языковое выражение, относительно которого можно утверждать, что оно либо истинно (True), либо ложно (False). Вместо слов True и False часто употребляются числа 1 и 0 соответственно.
Пример 4.1. Имеем два высказывания: «Дважды два четыре» и «3+5=9». Первое высказывание имеет истинное значение, а второе – ложное.
Если отвлечься от смысла высказывания, его можно обозначить буквой и рассматривать как переменную. Используя логические связки: «НЕ», «И», «ИЛИ», «ЕСЛИ ..., ТО...» и другие – можно из одних высказываний строить новые высказывания. Построение из заданных высказываний нового высказывания называется логической операцией.
Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д. В алгебре логики логические операции чаще всего описываются с помощью таблиц истинности. Для одноместной операции «не» («инверсия») таблица истинности выглядит так.
Таблица 4.1.
| «А» | «не А» |
«Не А» обозначается как  А, или Ā, или ~А, или !A. В табл. 2.2 приведены основные двухместные логические операции.
А, или Ā, или ~А, или !A. В табл. 2.2 приведены основные двухместные логические операции.
Таблица 4.2
| Обозначение логической операции | Другие обозначения логической операции | Набор истинностных значений | Название логической операции и связки | Как читается выражение |
А 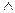 B B
| А & B
А B
АB
min (А, B) B
АB
min (А, B)
| Конъюнкция, логическое умножение, логическое «И» | А и B | |
А 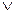 B B
| А+B max (А, B) | Дизъюнкция, логическое сложение, логическое «ИЛИ» | А или B | |
А 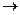 B B
| А 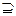 B
А B
А  B B
| Импликация, логическое следование | Если А, то B; А имплицирует B; А влечет B | |
А  B B
| А~ B
А  B
А B
А 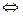 B B
| Эквиваленция, эквивалентность, равнозначность, тождественность | А тогда и только тогда, когда B; А эквивалентно B | |
А 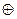 B B
| А+B
А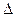 B B
| Сумма по модулю 2, разделительная дизъюнкция, разделительное «ИЛИ» | А плюс B; либо А, либо B | |
| А | B |
А 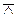 B B
| Штрих Шеффера, антиконъюнкция | Неверно, что А и B; А штрих Шеффера B | |
А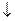 B B
|
А 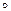 B
А B
А  B B
| Стрелка Пирса, антидизъюнкция, функция Вебба, ф-я Даггера | Ни А, ни B; А стрелка Пирса B |
Набор истинностных значений 0001 в первой строке таблицы соответствует результатам операций:
0  0 = 0;
0 = 0;
0  1 = 0;
1 = 0;
1  0 = 0;
0 = 0;
1  1 = 1.
1 = 1.
Как известно, в арифметике вначале выполняются операции умножения или деления, а затем – сложения или вычитания. Логические связки также подчиняются подобному правилу. Приоритет применения связок возрастает в следующем порядке: 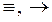 ,
, ,
, ,
,  . Чтобы изменить этот порядок, то, как и в арифметике, необходимо использовать скобки.
. Чтобы изменить этот порядок, то, как и в арифметике, необходимо использовать скобки.
Переменные и формулы в исчислении высказываний
1) выражение, состоящее только из пропозициональной переменной, является пропозициональной формулой; 2) если A и B – пропозициональные формулы, то каждое из выражений A, (AB),… 3) последовательность символов только тогда является пропозициональной формулой, когда она построена в соответствии с…Булевы функции
Особое значение имеют так называемые элементарные булевы функции. Двухместными элементарными булевыми функциями являются конъюнкция, дизъюнкция,… Имеются две одноместные булевы функции, зависящие от x: тождественная функция…Предикаты
Индивидная (или предметная) переменная представляет собой знак, обозначающий произвольный индивид из некоторого непустого подмножества множества… Пусть – индивиды из предметной области I. Рассмотрим какое-либо высказывание… Возьмем предметные переменные (с областями изменения соответственно; здесь – подмножество множества I, ). Выражение…Семантика исчисления предикатов
Английское слово «predicate» переводится на русский язык как «сказуемое». Рассмотрим предложение: «Гамлет пронзил Лаэрта мечом». В нем слово… пронзил(гамлет, лаэрт, меч). (4.1) Здесь пронзил– это предикат, а гамлет, лаэрт, меч – его термы. Такая запись похожа на обозначение функции, пронзил–…Равно(плюс(два, три), пять)
X(личность(Х)любит(Х, грибы)) «Никто не любит платить налоги» X любит(Х, платить(налоги))Правила логического вывода
Одним из наиболее важных правил логического вывода является «MODUS PONENS» (переводится с латинского как «правило отделения»). Другие полезные… · Если известно, что предложения A и AB истинны, то модус поненс позволяет… · Согласно правилу вывода модус толленс, если известно, что AB является истинным и B ложно, то можно вывести…Правило резолюции
. Предложения PAC и QBC называются резольвируемыми (или родительскими),… Правило резолюции является более общим правилом логического вывода по сравнению с рассмотренными ранее. Модус поненс и…Лекция № 5. МНОЖЕСТВА И ПОДМНОЖЕСТВА
Задание множеств
Если объект 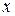 является элементом множества
является элементом множества 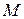 , то говорят, что
, то говорят, что 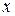 принадлежит
принадлежит 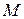 . Обозначение
. Обозначение 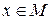 . В противном случае говорят, что
. В противном случае говорят, что 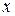 не принадлежит
не принадлежит 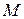 . Обозначение
. Обозначение 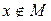 .
.
Множество, не содержащее элементов, называется пустым. Обозначение:  .
.
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами.
· Перечислением элементов:  .
.
· Характеристическим предикатом: 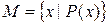 .
.
· Порождающей процедурой: 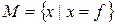 .
.
При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Характеристический предикат (от латинского praedicatum) – это некоторое условие, выраженное в форме логического утверждения, возвращающего логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит. Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.
Пример 5.1. 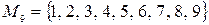 ;
;
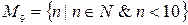 ;
;
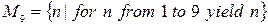 .
.
Парадокс Рассела
Если множество существует, то мы должны иметь возможность ответить на следующий вопрос: ? Пусть , тогда . Пусть , тогда . Получается неустранимое… 1. Ограничить используемые характеристические предикаты видомСравнение множеств
Мощность множества обозначается как . Для конечных множеств мощность – это число элементов. Например, , но . Если , то множества и называются… Иногда в литературе вместо мощности множества используется другой равнозначный…Операции над множествами
Обычно рассматриваются следующие операции над множествами:
· Объединение: 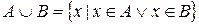 .
.
· Пересечение: 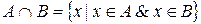 .
.
· Разность: 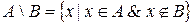 .
.
· Симметрическая разность:
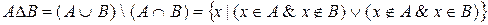 .
.
· Дополнение: 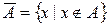 .
.
Операция дополнения подразумевает некоторый универсум:
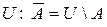 .
.
· Декартово произведение множеств:
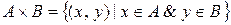 .
.
Декартово произведение двух множеств 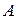 и
и  есть множество всех упорядоченных пар (x, y), где
есть множество всех упорядоченных пар (x, y), где 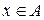 и
и 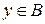 .
.
Пример 5.2. Пусть 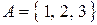 ,
, 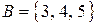 . Тогда
. Тогда
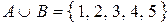 ,
, 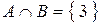 ,
, 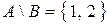 ,
, 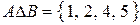 .
.
На рис. 5.1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Сами исходные множества изображаются геометрическими фигурами (бесконечные множества точек на плоскости), результат выделяется с помощью штриховки.

Рис. 5.1. Диаграммы Эйлера
Свойства операций над множествами
1. Инволютивность: ; 2. Идемпотентность:Булеан
Множество всех подмножеств множества 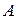 называется булеаном.
называется булеаном.
Теорема 5.1. Множество из n элементов имеет 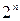 подмножеств.
подмножеств.
Доказательство: Эту теорему можно доказать разными способами (так же, как и многие другие теоремы). Мы докажем ее, используя бинарные представления чисел. Предположим, что мы имеем множество из трех элементов 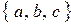 . Каждое подмножество этого множества зашифруем с помощью бинарного кода. Этот код будет состоять из трех бит (по количеству членов исходного множества). Если в рассматриваемом подмножестве присутствует элемент
. Каждое подмножество этого множества зашифруем с помощью бинарного кода. Этот код будет состоять из трех бит (по количеству членов исходного множества). Если в рассматриваемом подмножестве присутствует элемент  , первому биту кода присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент
, первому биту кода присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент  , второму биту присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент
, второму биту присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент 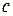 , третьему биту присваиваем значение единицы, в противном случае – нуля. Рассматривая все возможные подмножества исходного множества
, третьему биту присваиваем значение единицы, в противном случае – нуля. Рассматривая все возможные подмножества исходного множества 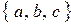 , включая пустое множество
, включая пустое множество 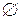 , получим следующий результат.
, получим следующий результат.
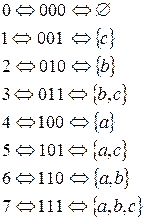
Как можно видеть, подмножества множества 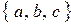 соответствуют восьми числам: 0, 1, …, 7. Мы рассмотрели все бинарные комбинации в пределах трех бит. Как известно, количество таких комбинаций равно
соответствуют восьми числам: 0, 1, …, 7. Мы рассмотрели все бинарные комбинации в пределах трех бит. Как известно, количество таких комбинаций равно 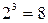 .
.
Применяя данный метод к множеству из четырех элементов, получим количество подмножеств: 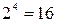 . Для множества из пяти элементов:
. Для множества из пяти элементов: 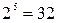 . Обобщая эти результаты, приходим к выводу, что множество из n элементов имеет
. Обобщая эти результаты, приходим к выводу, что множество из n элементов имеет 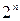 подмножеств.
подмножеств.
Проблема континуума
Лекция № 6. МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ
Сумма нечетных чисел
1 = 1 1+3 = 4 1+3+5 = 9Сумма натуральных чисел
. Таким образом, сумма первых n положительных целых чисел также обладает… Необходимо заметить, что метод индукции позволяет проверять уже известные формулы, но не позволяет выводить новые…Снова считаем подмножества
Добавление еще одного элемента в исходное множество приведет к тому, что появятся новые подмножества. Всего таких новых подмножеств будет ,… . Таким образом, наш результат подтверждает теорему 5.1.Биномиальные коэффициенты
, , .Треугольник Паскаля
Бином Ньютона для дробных и отрицательных показателей
В этом, более общем, случае формула бинома Ньютона начинается так же, как и формула (4.1), биномиальным коэффициентом служит выражение: , которое в случае целого положительного n, обращается в нуль при всяком , вследствие чего формула (6.1) содержит лишь…Гамма-функция
. По сути, факториал является функцией аргумента n. Однако это дискретная… Возникает вопрос: существует ли непрерывная функция непрерывного аргумента n, которая в частных случаях целого…Лекция № 7. КОМБИНАТОРИКА
Введение
Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Раздел математики, который их изучает, называется комбинаторикой.
Одними из наиболее важных понятий комбинаторики являются размещения и сочетания.
Способ расположения в определенном порядке некоторого числа элементов из заданного множества, когда существенна последовательность выбора элементов, называется размещением. Если же последовательность выбора элементов несущественна, то способ выбора называется сочетанием.
Пример 7.1. Дано множество S, состоящее из трех элементов: a, b, c. Необходимо определить количество комбинаций по два элемента из представленных трех.
1. Повторение элементов не допускается:
а) существует 6 размещений (ab, ac, ba, bc, ca, cb);
б) существует 3 сочетания (ab, bc, ca).
2. Повторение элементов разрешается:
а) существует 9 размещений (aa, ab, ac, ba, bb, bc, ca, cb, cc);
б) существует 6 сочетаний (aa, ab, ac, bb, bc, cc).
Размещения без повторений
Теорема 7.1. . (7.1) Доказательство. Задача сводится к заполнению k пустых мест символами элементов (рис. 7.1).Сочетания без повторений
Теорема 7.2. (7.2) Доказательство. Очевидно, что , поскольку одному сочетанию элементов… С учетом формулы (7.1) формулу (7.2) можно записать следующим образом:Размещения с повторением
Теорема 7.3. Общее число размещений с повторениями k элементов, взятых из совокупности n различных элементов, равно . Доказательство. Задача… Пример 7.4. Максимальное число знаков, которые могут быть представлены с… Пример 7.5. Код Бодо (Жан Морис Эмиль Бодо (1845-1903) – французский изобретатель в области телеграфии) использует для…Сочетания с повторением
. (7.5) Доказательство. Сведем задачу к случаю сочетаний без повторений. Для этого… Поэтому количество добавленных элементов не может быть равно k (или превосходить это число). Однако легко построить…Формула Стирлинга
. (7.6) Погрешность такого приближения определяется формулой . (7.7)Подстановки
, . Произведением подстановок и называется их суперпозиция . Суперпозиция – это… .Лекция № 8. ЧИСЛА ФИБОНАЧЧИ И ПРОСТЫЕ ЧИСЛА
Задача Фибоначчи
Нужно определить, сколько кроликов будет на ферме через n месяцев, если в начальный момент времени был только один новорожденный кролик. Очевидно, что фермер имеет одного кролика в первый месяц и одного кролика – во… Можно построить алгоритм, позволяющий найти при любом n.Сумма чисел Фибоначчи
0 = 0, 0+1 = 1, 0+1+1 = 2,Формула для чисел Фибоначчи
. Доказательство. Убедимся в справедливости этой формулы для n = 0, 1, а затем…Простые числа
Свойства простых чисел и их связь со всеми натуральными числами изучалась Евклидом (3 век до нашей эры). Если выписывать простые числа подряд, то… Среди простых чисел попадаются пары таких, разность между которыми равна двум… Евклид считал очевидным, что с помощью умножения только простых чисел можно получить все натуральные числа, причем…Лекция № 9. КОДИРОВАНИЕ
Введение
Вопросы кодирования издавна играли заметную роль в математике. Десятичная позиционная система счисления – это способ кодирования натуральных чисел. Римские цифры – другой способ кодирования натуральных чисел, причем гораздо более наглядный и естественный: палец – I, пятерня – V, две пятерни – X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен позиционной десятичной системой. Любопытно, что у римлян не было символа для обозначения нуля.
Декартовы координаты – способ кодирования геометрических объектов числами.
Задачу кодирования можно сформулировать следующим образом, Пусть заданы алфавиты 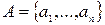 ,
, 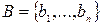 и функция
и функция 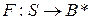 , где
, где 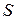 – некоторое множество слов в алфавите
– некоторое множество слов в алфавите 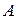 ,
, 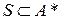 . Тогда функция
. Тогда функция 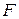 называется кодированием, элементы множества
называется кодированием, элементы множества 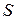 – сообщениями, а элементы
– сообщениями, а элементы 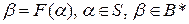 – кодами соответствующих сообщений.
– кодами соответствующих сообщений.
Обратная функция 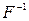 (если она существует) называется декодированием.
(если она существует) называется декодированием.
Если 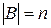 , то
, то 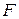 называется n-ичным кодированием. Наиболее распространенный случай
называется n-ичным кодированием. Наиболее распространенный случай 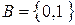 – двоичное кодирование. Именно этот случай рассматривается далее.
– двоичное кодирование. Именно этот случай рассматривается далее.
Алфавитное кодирование
Пусть задано конечное множество , которое называется алфавитом. Элементы алфавита называются буквами. Последовательность букв называется словом.… Пустое слово обозначается . Если , то называется началом, или префиксом, слова , а – окончанием, или постфиксом, слова . Если при этом…Разделимые схемы
Рассмотрим схему алфавитного кодирования 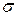 и различные слова, составленные из элементарных кодов. Схема
и различные слова, составленные из элементарных кодов. Схема 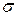 называется разделимой, если
называется разделимой, если
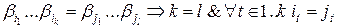 ,
,
то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование.
Схема 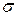 называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы:
называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы:
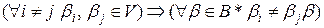 .
.
Теорема 9.1. Префиксная схема является разделимой.
Доказательство. От противного. Пусть кодирование со схемой 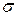 не является разделимым. Тогда существует такое слово
не является разделимым. Тогда существует такое слово 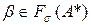 , что
, что
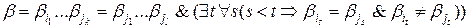 .
.
Поскольку 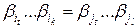 , значит,
, значит, 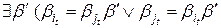 , но это противоречит тому, что схема префиксная.
, но это противоречит тому, что схема префиксная.
Замечание. Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы.
Пример 9.2. Разделимая, но не префиксная схема: 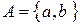 ,
, 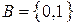 ,
, 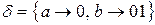 .
.
Чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению, известному как неравенство Макмиллана.
Теорема 9.2. Если схема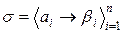 разделима, то
разделима, то
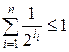 , где
, где 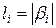 .
.
Доказательство. Обозначим: 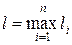 . Рассмотрим n-ю степень левой части неравенства
. Рассмотрим n-ю степень левой части неравенства 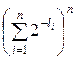 . Раскрывая скобки, имеем сумму
. Раскрывая скобки, имеем сумму 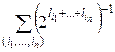 , где
, где 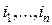 – различные наборы номеров элементарных кодов. Обозначим через
– различные наборы номеров элементарных кодов. Обозначим через 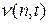 количество входящих в эту сумму слагаемых вида
количество входящих в эту сумму слагаемых вида 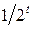 , где
, где 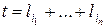 . Для некоторых
. Для некоторых 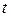 может быть
может быть 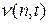 =0. Приводя подобные, имеем сумму
=0. Приводя подобные, имеем сумму 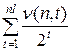 . Каждому слагаемому вида
. Каждому слагаемому вида  можно однозначно сопоставить код (слово в алфавите B) вида
можно однозначно сопоставить код (слово в алфавите B) вида 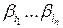 . Это слово состоит из n элементарных кодов и имеет длину t.
. Это слово состоит из n элементарных кодов и имеет длину t.
Таким, образом, 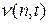 – это число некоторых слов вида
– это число некоторых слов вида 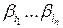 , таких что
, таких что 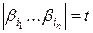 . В силу разделимости схемы
. В силу разделимости схемы 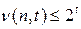 , в противном случае заведомо существовали бы два одинаковых слова
, в противном случае заведомо существовали бы два одинаковых слова 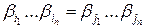 , допускающих различное разложение. Имеем
, допускающих различное разложение. Имеем
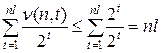 .
.
Следовательно, 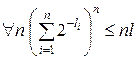 , и значит,
, и значит, 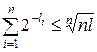 , откуда
, откуда
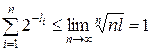 .
.
Неравенство Макмиллана является не только необходимым, но и достаточным условием разделимости схемы алфавитного кодирования.
Пример 9.3. Азбука Морзе – это схема алфавитного кодирования 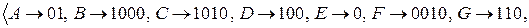

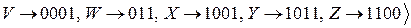 ,
,
где по историческим и техническим причинам 0 называется точкой, а 1 называется тире. Имеем
1/4+1/16+1/16+1/8+1/2+1/16+1/8+1/16+1/4+1/16+1/8+1/16+1/4+1/4+
+1/8+1/16+1/16+1/8+1/8+1/2+1/8+1/16+1/8+1/16+1/16+116=
=2/2+4/4+7/8+12/16=3+5/8 > 1.
Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта схема не является разделимой. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщения. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.
Помехоустойчивое кодирование
, где S – множество переданных, а – соответствующее множество принятых по каналу… ,Лекция № 10. ШИФРОВАНИЕ
Введение
Шифрование – это кодирование данных с целью защиты от несанкционированного доступа. Область знаний о шифрах, методах их создания и раскрытия называется криптографией (или тайнописью).
Криптография известна с глубокой древности и использует самые разнообразные шифры, как чисто информационные, так и механические. В настоящее время наибольшее практическое значение имеет защита данных в компьютере, поэтому далее рассматриваются программные шифры для сообщений в алфавите {0,1}.
Начнем с определения операции: 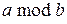 . Здесь операнды: a и b – целые числа, а результат данной операции – остаток, возникающий при целочисленном делении a на b.
. Здесь операнды: a и b – целые числа, а результат данной операции – остаток, возникающий при целочисленном делении a на b.
Пример 10.1.
15 2 =
2 = 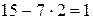 ,
,
26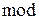 3 =
3 = 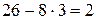 ,
,
32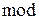 4 =
4 = 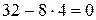 .
.
Пусть имеется генератор псевдослучайных чисел, работающий по определенному алгоритму. Часто используется следующий алгоритм:
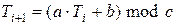 , (10.1)
, (10.1)
где 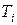 – предыдущее псевдослучайное число,
– предыдущее псевдослучайное число, 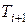 – последующее псевдослучайное число, а коэффициенты a, b, c постоянны и хорошо известны. Обычно c=
– последующее псевдослучайное число, а коэффициенты a, b, c постоянны и хорошо известны. Обычно c=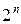 , где
, где  – разрядность процессора,
– разрядность процессора, 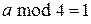 , а b – нечетное. В этом случае последовательность псевдослучайных чисел имеет период c.
, а b – нечетное. В этом случае последовательность псевдослучайных чисел имеет период c.
Пример 10.2.В табл. 10.1 приведены результаты расчетов по формуле (10.1) для различных ключей шифра 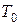 и коэффициентов: a=81, b=9, c=65536.
и коэффициентов: a=81, b=9, c=65536.
Таблица 10.1
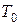
| 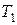
| 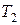
| 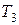
| 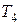
| 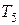
| 
| 
| 
| 
| 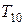
|
Процесс шифрования определяется следующим образом. Шифруемое сообщение представляется в виде последовательности слов 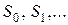 , каждое длины
, каждое длины  , которые складываются по модулю два со словами последовательности
, которые складываются по модулю два со словами последовательности 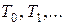 , то есть
, то есть
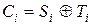 .
.
Последовательность 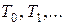 называется гаммой шифра. Процесс расшифровывания заключается в том, чтобы еще раз сложить шифрованную последовательность с той же самой гаммой шифра:
называется гаммой шифра. Процесс расшифровывания заключается в том, чтобы еще раз сложить шифрованную последовательность с той же самой гаммой шифра:
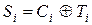 .
.
Ключом шифра является начальное значение 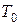 , которое является секретным и должно быть известно только отправителю и получателю шифрованного сообщения. Шифры, в которых для зашифровки и расшифровки используется один и тот же ключ, называются симметричными.
, которое является секретным и должно быть известно только отправителю и получателю шифрованного сообщения. Шифры, в которых для зашифровки и расшифровки используется один и тот же ключ, называются симметричными.
Описанный метод шифрования обладает существенным недостатком. Если известна хотя бы часть исходного сообщения, то все сообщение может быть легко дешифровано. Действительно, пусть известно одно исходное слово 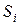 . Тогда
. Тогда
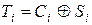 ,
,
и далее вся правая часть гаммы шифра определяется по указанной формуле генератора псевдослучайных чисел.
Для повышения криптостойкости симметричных шифров применяются различные приемы.
· Вычисление гаммы шифра по ключу более сложным (или секретным) способом.
· Применение вместо 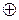 более сложной (но обратимой операции) для вычисления шифровки.
более сложной (но обратимой операции) для вычисления шифровки.
· Предварительное перемешивание битов исходного сообщения по фиксированному алгоритму.
В настоящее время широкое распространение получили шифры с открытым ключом. Эти шифры не являются симметричными – для зашифровки и расшифровки используются разные ключи. При этом ключ, используемый для зашифровки, является открытым (не секретным) и может быть сообщен всем желающим отправить шифрованное сообщение. А ключ, используемый для расшифровки, является закрытым и хранится в секрете получателем шифрованных сообщений. Даже знание всего зашифрованного сообщения и открытого ключа, с помощью которого оно было зашифровано, не позволяет дешифровать сообщение без знания закрытого ключа.
Для описания метода шифрования с открытым ключом нужны некоторые факты из теории чисел, изложенные (без доказательства) в следующем разделе.
Модулярная арифметика
. Отношение сравнимости рефлексивно, симметрично и транзитивно и является… Над вычетами (по модулю n) определены операции сложения и умножения по модулю n, обозначаемые соответственно и , и…Пример 10.3.
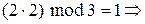
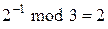 ,
,
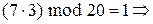
 ,
,
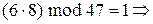
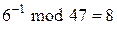 .
.
Функция: 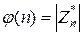 – называется функцией Эйлера. Если
– называется функцией Эйлера. Если 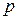 – простое число, то
– простое число, то 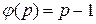 , и вообще
, и вообще 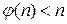 .
.
Можно показать, что
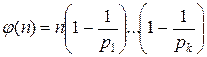 ,
,
где 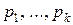 – все простые делители n.
– все простые делители n.
Пример 10.4.
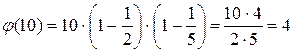 ,
,
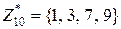 ,
, 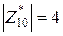 .
.
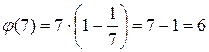 ,
,
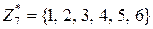 ,
, 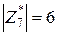 .
.
Теорема 10.1. (Эйлера). Если 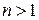 , то
, то 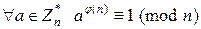 .
.
Пример 10.5.Пустьn=10. Тогда 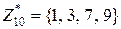 и
и 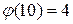 .
.
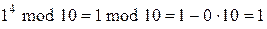 ,
,
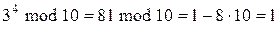 ,
,
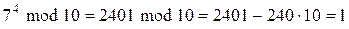 ,
,
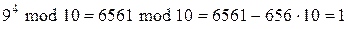 .
.
Из теоремы Эйлера непосредственно выводима
Теорема 10.2. (малая теорема Ферма). Если 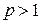 , то
, то 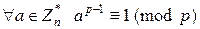 .
.
Имеет место следующее утверждение
Теорема 10.3. Если числа 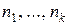 попарно взаимно простые, число
попарно взаимно простые, число 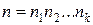 – их произведение, x и a – целые числа, то
– их произведение, x и a – целые числа, то 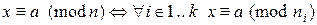 .
.
Последнее утверждение является следствием теоремы, которая известна как «китайская теорема об остатках».
Пример 10.6.Пустьn=10=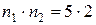 ; x=81; a=61. Тогда
; x=81; a=61. Тогда
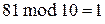 ,
, 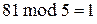 ,
, 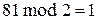 ,
,
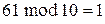 ,
, 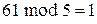 ,
, 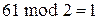 .
.