Examples Commutative operations in mathematics

Two well-known examples of commutative binary operations:^[7]

· The addition of real numbers is commutative, since

For example 4 + 5 = 5 + 4, since both expressions equal 9.

· The multiplication of real numbers is commutative, since

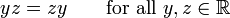
For example, 3 × 5 = 5 × 3, since both expressions equal 15.

11. In mathematics, especially order theory, a partially ordered set (or poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the set, one of the elements precedes the other. Such a relation is called a partial order to reflect the fact that not every pair of elements need be related: for some pairs, it may be that neither element precedes the other in the poset. Thus, partial orders generalize the more familiar total orders, in which every pair is related. A finite poset can be visualized through its Hasse diagram, which depicts the ordering relation.^[1]

A familiar real-life example of a partially ordered set is a collection of people ordered by genealogical descendancy. Some pairs of people bear the descendant-ancestor relationship, but other pairs bear no such relationship.

A partial order is a binary relation "≤" over a set P which is antisymmetric, transitive, and either reflexive or irreflexive, i.e., for all a, b, and c in P, we have that:

· Either: a ≤ a (reflexivity) for all a in P, or: a ≰ a (irreflexivity) for all a in P;

· if a ≤ b and b ≤ a then a = b (antisymmetry);

· if a ≤ b and b ≤ c then a ≤ c (transitivity).

In other words, a partial order is an antisymmetric preorder.

A set with a partial order is called a partially ordered set (also called a poset). The term ordered set is sometimes also used for posets, as long as it is clear from the context that no other kinds of orders are meant. In particular, totally ordered sets can also be referred to as "ordered sets", especially in areas where these structures are more common than posets.

For a, b, elements of a partially ordered set P, if a ≤ b or b ≤ a, then a and b are comparable. Otherwise they are incomparable. A partial order under which every pair of elements is comparable is called a total order or linear order; a totally ordered set is also called a chain (e.g., the natural numbers with their standard order). A subset of a poset in which no two distinct elements are comparable is called an antichain.

Linear order -A set with an ordering ≤ such that for any two elements a and b either a≤b or b≤a.

In this chapter we prove some results about linearly ordered sets which form a useful

background in much of set theory. Among these facts are: any two denumerable densely

ordered sets are isomorphic, the existence of ηα sets, the existence of completions, and a

discussion of Suslin lines.

A linearly ordered set (A, <) is densely ordered iff |A| > 1, and for any a < b in A

there is a c ∈ A such that a < c < b. A subset X of a linearly ordered set L is dense in L

iff for any two elements a < b in L there is an x ∈ X such that a < x < b. Note that if X

is dense in L and L has at least two elements, then L itself is dense.

Theorem 7.1. If L is a dense linear order, then L is the disjoint union of two dense

subsets.

12. In mathematics, an equivalence relationis a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent (with respect to the equivalence relation) if and only if they are elements of the same cell. The intersection of any two different cells is empty; the union of all the cells equals the original set. A given binary relation ~ on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive. Equivalently, for all a, b and c in A:

· a ~ a. (Reflexivity)

· if a ~ b then b ~ a. (Symmetry)

· if a ~ b and b ~ c then a ~ c. (Transitivity)

A together with the relation ~ is called a setoid. The equivalence class of a under ~, denoted [a], is defined as .