рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Definitions
Реферат Курсовая Конспект
Definitions
Definitions - раздел Математика, A set in mathematics is a collection of well defined and distinct objects, considered as an object in its own right A Linear Order On A Set S Is A (Binary) Relation <...
A linear order on a set S is a (binary) relation < with the following properties:
- irreflexivity: x≮x;
- asymmetry: x<y and y<x cannot both be true;
- transitivity: if x<y<z, then x<z;
- comparison: if x<z, then x<y or y<z;
- connectedness: if x≮y and y≮x, then x=y.
In classical mathematics, one may see these versions of asymmetry and connectedness:
- x≮y or y≮x;
- x<y or y<x or x=y.
15. In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x < y, there is a z in X such that x < z < y.
The rational numbers with the ordinary ordering are a densely ordered set in this sense, as are the real numbers. On the other hand, the ordinary ordering on the integers is not dense.
Any binary relation R is said to be dense if, for all R-related x and y, there is a z such that x and z and also z and y are R-related.[citation needed] Formally:

Every reflexive relation is dense. A strict partial order < is a dense order iff < is a dense relation.
16. First-order logic is a formal system used in mathematics , philosophy , linguistics , and computer science At its core, mathematical logic deals with mathematical concepts expressed using formal logical systems. These systems, though they differ in many details, share the common property of considering only expressions in a fixed formal language, or signature. The systems of propositional logic and first-order logic are the most widely studied today, because of their applicability tofoundations of mathematics and because of their desirable proof-theoretic properties.[3] Stronger classical logics such as second-order logic or infinitary logic are also studied, along with nonclassical logics such as intuitionistic logic.
First-order logic is a particular formal system of logic. Its syntax involves only finite expressions as well-formed formulas, while its semantics are characterized by the limitation of all quantifiersto a fixed domain of discourse.
Early results about formal logic established limitations of first-order logic. The Löwenheim–Skolem theorem (1919) showed that if a set of sentences in a countable first-order language has an infinite model then it has at least one model of each infinite cardinality. This shows that it is impossible for a set of first-order axioms to characterize the natural numbers, the real numbers, or any other infinite structure up to isomorphism. As the goal of early foundational studies was to produce axiomatic theories for all parts of mathematics, this limitation was particularly stark.
Gödel's completeness theorem (Gödel 1929) established the equivalence between semantic and syntactic definitions of logical consequence in first-order logic. It shows that if a particular sentence is true in every model that satisfies a particular set of axioms, then there must be a finite deduction of the sentence from the axioms. The compactness theorem first appeared as a lemma in Gödel's proof of the completeness theorem, and it took many years before logicians grasped its significance and began to apply it routinely. It says that a set of sentences has a modelif and only if every finite subset has a model, or in other words that an inconsistent set of formulas must have a finite inconsistent subset. The completeness and compactness theorems allow for sophisticated analysis of logical consequence in first-order logic and the development of model theory, and they are a key reason for the prominence of first-order logic in mathematics.
Gödel's incompleteness theorems (Gödel 1931) establish additional limits on first-order axiomatizations. The first incompleteness theorem states that for any sufficiently strong, effectively given logical system there exists a statement which is true but not provable within that system. Here a logical system is effectively given if it is possible to decide, given any formula in the language of the system, whether the formula is an axiom. A logical system is sufficiently strong if it can express the Peano axioms. When applied to first-order logic, the first incompleteness theorem implies that any sufficiently strong, consistent, effective first-order theory has models that are not elementarily equivalent, a stronger limitation than the one established by the Löwenheim–Skolem theorem. The second incompleteness theorem states that no sufficiently strong, consistent, effective axiom system for arithmetic can prove its own consistency, which has been interpreted to show that Hilbert's program cannot be completed.
The signature of a structure consists of a set of function symbols and relation symbols along with a function that ascribes to each symbol s a natural number 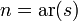 which is called the arity of s because it is the arity of the interpretation of s.
which is called the arity of s because it is the arity of the interpretation of s.
Since the signatures that arise in algebra often contain only function symbols, a signature with no relation symbols is called an algebraic signature. A structure with such a signature is also called an algebra; this should not be confused with the notion of an algebra over a field.
17. In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth. In classical logic, with its intended semantics, the truth values are true (1 or T) and false (0 or ⊥); that is, classical logic is a two-valued logic. This set of two values is also called the Boolean domain. Corresponding semantics of logical connectives are truth functions, whose values are expressed in the form of truth tables. Logical biconditional becomes the equality binary relation, and negation becomes a bijection which permutes true and false. Conjunction and disjunction are dual with respect to negation, which is expressed by De Morgan's laws:
¬(p∧q) ⇔ ¬p ∨ ¬q
¬(p∨q) ⇔ ¬p ∧ ¬q
Propositional variables become variables in the Boolean domain. Assigning values for propositional variables is referred to as valuation.
| T true | ·∧· conjunction | ||
| ¬ | |||
| ⊥ false | ·∨· |
Logical disjunction is an operation on two logical values, typically the values of two propositions, that produces a value of false if and only if both of its operands are false. More generally a disjunction is a logical formula that can have one or more literals separated only by ORs. A single literal is often considered to be a degenerate disjunction.
The disjunctive identity is 0, which is to say that OR-ing an expression with 0 will never change the value of the expression. In keeping with the concept of vacuous truth, when disjunction is defined as an operator or function of arbitrary arity, the empty disjunction (OR-ing over an empty set of operands) is often defined as having the result 0.
The set of terms is inductively defined by the following rules:
1. Variables. Any variable is a term.
2. Functions. Any expression f(t1,...,tn) of n arguments (where each argument ti is a term and f is a function symbol of valence n) is a term. In particular, symbols denoting individual constants are 0-ary function symbols, and are thus terms.
Only expressions which can be obtained by finitely many applications of rules 1 and 2 are terms. For example, no expression involving a predicate symbol is a term.
– Конец работы –
Эта тема принадлежит разделу:
A set in mathematics is a collection of well defined and distinct objects, considered as an object in its own right
A is a proper subset of B and conversely B is a proper superset of A... In set theory and related branches of mathematics a collection F of subsets... If every member of set A is also a member of set B then A is said to be a subset of B written A B A is...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Definitions
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов