Системы линейных алгебраических уравнений
Определители:
Вычисление определителя порядка п=2:
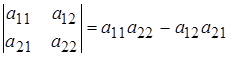
порядка п=3 (и выше):
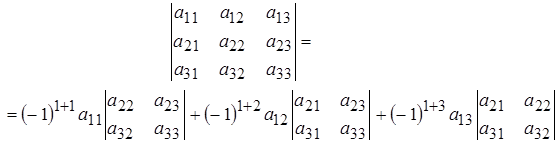
(аналогичное разложение допустимо для любой строки или столбца)
Системы линейных алгебраических уравнений
Метод Крамера
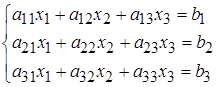
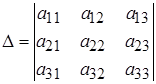 ,
,  ,
, 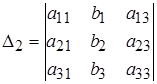 ,
, 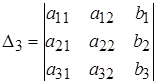
1) При 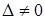 :
: 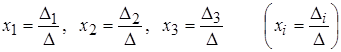 .
.
2) При 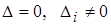 система несовместна.
система несовместна.
3) При  система требует исследования другими методами.
система требует исследования другими методами.
Метод Гаусса:
Расширенная матрица системы т уравнений с п неизвестными (составленная из всех коэффициентов и правых частей уравнений) приводится к треугольному виду с помощью элементарных преобразований над строками. При этом количество уравнений может уменьшиться с т до 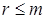 .
.
Число независимых (базисных) переменных определяется разностью между общим количеством переменных (п) и числом оставшихся в системе уравнений (r).Через n-r базисные переменные выражаются оставшиеся (зависимые) r переменные (начиная с нижнего, самого короткого уравнения).
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Коллинеарные векторы: || ||т, ||т (т – некоторая прямая) Компланарные векторы: ||ω, ||ω, ||ω (ω – некоторая… Ортогональная проекция вектора на вектор :ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Окрестность точки 
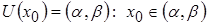
r-окрестность: 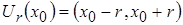

Ограниченные множества:
А ограничено сверху:  (верхняя граница):
(верхняя граница): 
А ограничено снизу  (нижняя граница):
(нижняя граница): 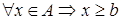
А ограничено  :
: 
Минимум множества: 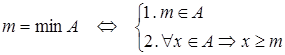
Максимум множества: 
Верхняя грань (точная верхняя граница) – наименьшая из верхних границ: 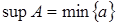
Нижняя грань (точная нижняя граница) – наибольшая из нижних границ: 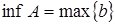
Последовательность: 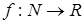 или
или 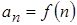
Монотонная последовательность:
возрастающая - 
убывающая - 
Ограниченная последовательность: 
Предел последовательности ап: 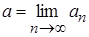
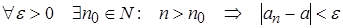
Если последовательность ограничена и монотонна, она сходится (имеет предел).
Сходящаяся последовательность ограничена.
Второй замечательный предел: 
Предел функции 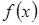 в точке
в точке 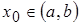
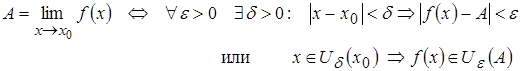
Бесконечно малые и бесконечно большие функции
Бесконечно малая функция 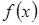 в точке
в точке 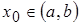 :
: 
Бесконечно большая функция 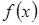 в точке
в точке 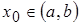 :
:


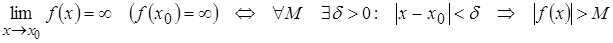
Теорема.  ;
; 
Сравнение бесконечно малых:
Если 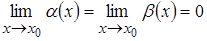 и
и 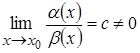 , то
, то 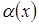 и
и 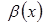 - бесконечно малые одного порядка.
- бесконечно малые одного порядка.
При с=1 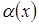 и
и 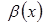 эквивалентны:
эквивалентны: 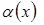 ~
~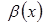 .
.
При с=0 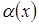 -бесконечно малая большего порядка малости относительно
-бесконечно малая большего порядка малости относительно 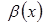
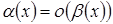
Первый замечательный предел: 
Следствия: (при  )
) 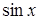 ~
~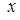 ,
,  ~
~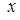 ,
, 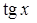 ~
~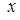 ,
,  ~
~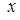
Второй замечательный предел: 
Следствия: (при  )
) 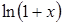 ~
~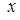 ,
, 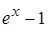 ~
~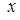
Непрерывность функции
Функция 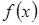 непрерывна в точке
непрерывна в точке 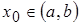 , если
, если 
Если х0 – точка разрыва, 
1. 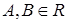 – х0 разрыв I рода, (В-А) – скачок (А=В – устранимый разрыв)
– х0 разрыв I рода, (В-А) – скачок (А=В – устранимый разрыв)
2.  – х0 разрыв II рода
– х0 разрыв II рода
ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Геометрически производная – угловой коэффициент касательной к графику…Таблица производных
1.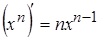 8.
8.
2.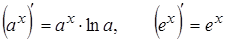 9.
9.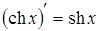
3.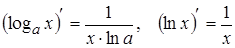 10.
10.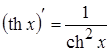
4. 11.
11.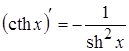
5.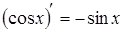 12.
12.
6.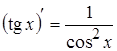 13.
13.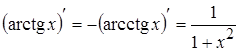
7.
Производная сложно-показательной функции 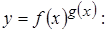

Дифференциал: 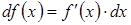 (где
(где 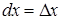 )
)
ТеоремаЛагранжа (формула конечных приращений):
 или
или 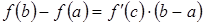
ТеоремаЛопиталя: 
Исследование функций
1.Если 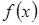 возрастает (убывает), то
возрастает (убывает), то 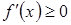
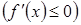 .
.
2.Если 
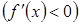 , то
, то 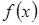 возрастает (убывает).
возрастает (убывает).
3.(т.Ферма) Если 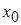 - т. extr, и существует
- т. extr, и существует  , то
, то  .
.
4.Если в т. 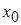
 , то при
, то при  (
( )
) 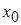 - т. min (
- т. min (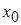 - т. max).
- т. max).
5.Если на 
 (
( ), то функция выпукла вниз (вверх).
), то функция выпукла вниз (вверх).
6.Наклонная асимптота y=kx+b, где 
Формула Тейлора
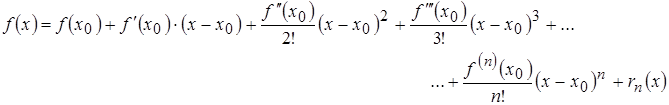
Формула Маклорена (х0=0):
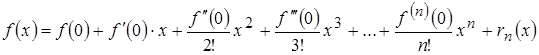
ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Таблица неопределенных интегралов
1. 
2. 
3. 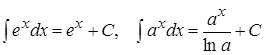
4.  8.
8. 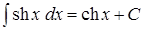
5.  9.
9. 
6.  10.
10. 
7.  11.
11. 
12. 
13. 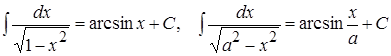
14. 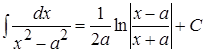 16.
16. 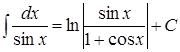
15. 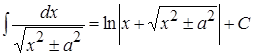 17.
17. 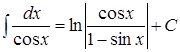
-------------------------------------------------------------------------------

Интегрирование по частям

Основные подстановки:
1.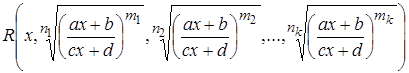 :
:
 , где
, где 
2. 
3. 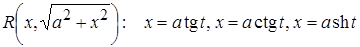
4. 
5. 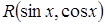 :
:  ,
, 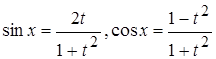 ,
, 
Применение определенного интеграла для вычисления площадей, длин, объемов
Площадь плоской фигуры
1.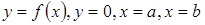 :
: 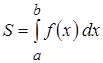
2. :
: 
3. :
: 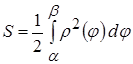
Длина дуги плоской кривой 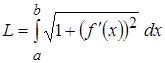
Объем тела вращения 
Площадь поверхности вращения 
Несобственные интегралы
Первого рода: 

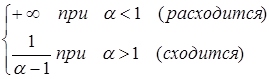
Второго рода: 

Признаки сходимости
1) Если неотрицательные функции 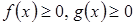 таковы, что
таковы, что  , то из сходимости
, то из сходимости  следует сходимость
следует сходимость  , а из расходимости
, а из расходимости  следует расходимость
следует расходимость  .
.
2) Если неотрицательные функции 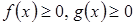 таковы, что
таковы, что 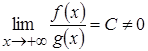 , то интегралы
, то интегралы  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Дифференцирование функции двух переменных
Градиент: 
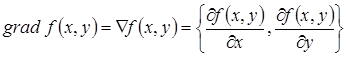
Производная по направлению 

Дифференциал функции двух переменных
Первого порядка: 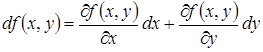
Второго порядка: 
Экстремум функции двух переменных
Локальный экстремум
 - т. max (min) функции
- т. max (min) функции  , если:
, если:
1. 
2. 
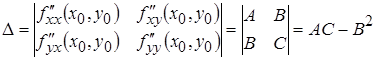
1) 
2) 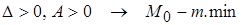
3) 
4)  - требуется дополнительное исследование
- требуется дополнительное исследование
Условный экстремум
Экстремумы функции  при дополнительном условии
при дополнительном условии 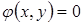 соответствуют экстремумам функции Лагранжа
соответствуют экстремумам функции Лагранжа  , которые находятся из условий
, которые находятся из условий
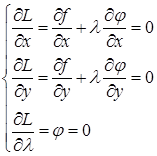
Числовой ряд 
Сумма ряда – предел последовательности частичных сумм:
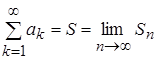 , где
, где 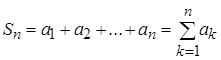
Необходимое условие сходимости – если ряд сходится, то  .
.
Достаточные признаки сходимости знакоположительных рядов ().