Математическая статистика
Математическая статистика.
Вариационный ряд.
Х1 – размер обуви; х1 – 35; 36; Х2 – рост;Таблица 1.
| 
| … | 
|
| 
| … | 
|
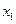
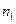
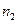
Можно также рассматривать частости для каждой варианты.
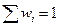
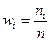
Замечание: частости являются аналогом вероятности.
Если значения признака не дискретны, т.е. заполняют некоторый интервал, то этот интервал разбивают на несколько возрастающих интервалов и получают так называемый интервальный вариационный ряд.
Таблица 2.
| 
| … | 
|
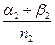
Любой интервальный ряд можно превратить в дискретный, используя вместо хi середины интервалов.
Числовые характеристики дискретного числового ряда.
Среднее значение (аналог математического ожидания).
(1) 
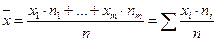
Дисперсия вариационного ряда (аналог дисперсии случайной величины).
(2) 
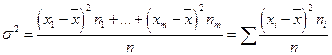
Среднее квадратическое отклонение вариационного ряда (аналог среднего квадратического отклонения случайной величины).
Свойства числовых характеристик вариационного ряда аналогичны свойствам характеристик случайных величин. Пример: Х – рост. 150-160 160-170 …Выборочный метод.
Определение: Пусть требуется изучить признак Х. Все элементы подлежащие изучению называются генеральной совокупностью.
Обозначение: N – количество элементов генеральной совокупности (объем генеральной совокупности).
На всей генеральной совокупности признак Х имеет следующий вариационный ряд.
Таблица 1.
|
|
| … |
|
| 
| … | 
|
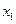
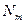
Вариационный ряд для всей генеральной совокупности называется генеральным вариационным рядом.
Характеристики генерального вариационного ряда называются генеральными характеристиками.
1. Генеральное среднее:
(1) 
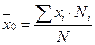
2. Генеральная дисперсия:
(2) 
3. Генеральное среднее квадратическое отклонение:
(3) 
4. Генеральная доля или вероятность признака:
(4) 
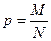
Как правило, распределение признака Х во всей генеральной совокупности неизвестно, т.е. неизвестен генеральный вариационный ряд, неизвестны все генеральные характеристики (формула 1-4).
Неизвестные параметры генеральной совокупности можно оценить с помощью результатов случайной выборки. Обследование всей генеральной совокупности бывает либо слишком дорого, либо практически невозможно (разрушаются элементы генеральной совокупности).
Определение: Часть элементов генеральной совокупности отобранных случайно называются случайной выборкой.
Количество элементов в выборке называется объемом выборки.
Выборка должна обладать свойством репрезентативности, т.е. она должна представлять всю генеральную совокупность. Для этого выборка должна отвечать следующим требованиям:
1. Выборка должна быть достаточно большой, чтобы проявились массовые закономерности.
2. Выборка должна быть случайной, чтобы каждый элемент генеральной совокупности мог иметь одинаковый с другими шанс попасть в выборку.
Существуют различные способы образования выборки (см. учебник).
Математическая статистика рассматривает собственно случайную выборку с повторным и бесповторным отбором членов. При повторном отборе элемент после обследования возвращается в генеральную совокупность, при бесповторном не возвращается. Бесповторная выборка более информативна, т.к. один и тот же элемент не может попасть в выборку дважды.
Пусть образована выборка объема n. В результате изучения признака Х на этой выборке получаем вариационный ряд, который называется выборочным вариационным рядом.
Таблица 2.
|
|
| … |
|
|
|
| … |
|
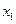
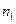
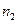
Все характеристики выборочного вариационного ряда называются выборочными характеристиками:
1. Выборочное среднее:
(5) 
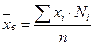
2. Выборочная дисперсия:
(6) 
3. Выборочная средняя квадратическая ошибка:
(7) 
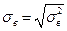
4. Выборочная доля или частость:
(8) 
Все характеристики выборочного вариационного ряда являются случайными величинами, т.к. отобраны случайным образом.
Точечные оценки.
Обозначение: θ (тэта). Определение: Оценкой неизвестного параметра θ называется случайная… Для практических целей вместо неизвестного параметра берут приближенно значение его оценки θ ≈ Х.Теоремы об оценках.
(9) (10)- повторная выборкаТребования к оценкам.
1. Оценка называется несмещенной, если математическое ожидание оценки совпадает с оцениваемыми параметрами, т.е.: (13) 2. Оценка называется состоятельной, если при достаточно большом объеме выборки n практически достоверно, что оценка…Средние квадратические ошибки.
Обозначение: (15) Определение: Среднеквадратической ошибкой для выборочной доли называется среднеквадратическое отклонение выборочной…Табл. 3 Среднеквадратические ошибки.
| Повторная выборка | Бесповторная выборка | |
| Средняя |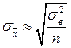 
| 
|
| Доля |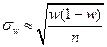 
| 
|
Замечания:
1. т.к.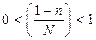 
, то средние квадратические ошибки для бесповторной выборки меньше, чем для повторной (если ошибки меньше, то они лучше, т.е. бесповторная выборка лучше, чем повторная);
2. если объем генеральной совокупности N очень велик, то 
. В этом случае результаты повторной и бесповторной выборок практически совпадают;
Доверительная вероятность.
Интервальное оценивание.
∆ - называется предельной ошибкой выборки, т.е. предельная ошибка выборки – max отклонение по модулю оценки от оцениваемого параметра, которое… Определение: Надежностью или доверительной вероятностью называется вероятность… (17) -доверительная вероятность (надежность).Доверительная вероятность при оценивании среднего значения.
Рассмотрим формулу *: Применим формулу * к выборочной средней. Получаем:Доверительная вероятность при оценивании генеральной доли (вероятности).
(19)- доверительная вероятность для оценки доли, где: Р – доверительная вероятность; w – выборочная доля, случайная величина, имеет нормальный закон распределения, оценка;Проверка гипотез.
Критерии согласия.
Формируется гипотеза Н0 о неизвестном законе распределения и по выборочным данным эта гипотеза либо отвергается либо принимается. Правило, по которому решается отвергнуть гипотезу Н0 или нет называется… Гипотеза Н0 может быть выдвинута не только о неизвестном законе распределения. Поскольку о признаке Х в генеральной…Проверка гипотезы о нормальном законе распределения.
Критерий согласия Пирсона (критерий согласия (хи)).
(1) , где - вероятность того, что случайная величина заключена в интервале . И эти… (2)Двумерная случайная величина.
Каждое значение двумерной случайной величины Z это упорядоченная пара чисел x и y. Вероятность этого значения это вероятность совместного… Пусть двумерная случайная величина Z принимает только дискретные значения, т.е. обе случайные величины x и y являются…Условные математические ожидания.
Если фиксировано значение , то условное математическое ожидание для y вычисляется по формуле: (5) Если фиксировано значение , то условное математическое ожидание для х определяется формулой:Виды зависимости между случайными величинами.
2. Статистическая – если каждому значению х соответствует целый ряд распределения значения y (и наоборот). Такая зависимость задается корреляционной… 3. Корреляционная – это функциональная зависимость между значениями одной… Частота или мера корреляционной зависимости определяется корреляционным моментом.Линейная регрессия.
Линейная корреляционная зависимость задается следующими уравнениями зависимости: (I) - I линейное уравнение регрессии y по х; (II) - II линейное уравнение регрессии х по y;Свойства коэффициента линейной корреляции.
2. r принимает значения от ; 3. если r = 0, то между х и y не существует линейной корреляционной… 4. чем ближе модуль r к 1, тем теснее линейная корреляционная связь;Нахождение параметров линейных уравнений регрессии методом наименьших квадратов.
- I - II Метод наименьших квадратов состоит в том, что неизвестные параметры a и b – I, c, d – II находятся из принципа…Свойства коэффициентов регрессии.
2. коэффициенты регрессии являются угловыми коэффициентами для соответствующих прямых I и II относительно соответствующих осей, поэтому, если μ… Замечание: Прямые регрессии пересекаются в точке А с координатами .Связь между коэффициентами корреляции и коэффициентами регрессии.
Сравнивая формулы 11, 12 и 13 получаем, что
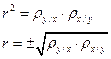, где значение r выбирается так, чтобы он совпадал со знаком μ.