рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Критерий согласия Пирсона (критерий согласия (хи)).

Реферат Курсовая Конспект

Выберите учебное заведение

Критерий согласия Пирсона (критерий согласия (хи)).

Критерий согласия Пирсона (критерий согласия (хи)). - раздел Математика, Математическая статистика Пусть Закон Распределения Случайной Величины Х Во Всей Генеральной Совокупнос...

Пусть закон распределения случайной величины Х во всей генеральной совокупности неизвестен. Образована выборка объема n. По результатам выборки получено значение . Данные выборки позволяют сформулировать гипотезу Н₀о том, что случайная величина Х имеет нормальный закон распределения с параметрами 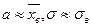. Для проверки этой гипотезы применяется критерий согласия Пирсона, статистика которого

(1) 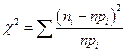, где

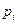- вероятность того, что случайная величина заключена в интервале 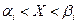. И эти вероятности вычислены с предположением, что гипотеза Н₀верна, т.е. Х имеет нормальный закон распределения с параметрами 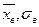. Тогда для вычисления 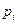можно применить формулу для нормального закона.

(2)

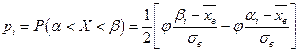
Случайная величина имеет известный закон распределения, который затабулирован на странице 558.

Значение , полученное по ф. (1) – опытное (эмпирическое), т.к. получено по результатам выборки.

Критическое значение находим по таблице стр. 558 и определяется двумя параметрами α и k, где

α – уровень значимости;

k – называется числом степеней свободы и равняется m = 3, где m – это количество интервалов признака в выборке.

Если 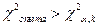, то (гипотеза о нормальном законе отвергается). В противном случае принимается.

Пример:

По результатам обследования 100 станков из 10000 для определения времени бесперебойной работы станка, получены данные, которые занесены в таблицу.

1) Проверить гипотезу Н₀ о нормальном законе распределения случайной величины Х – времени бесперебойной работы станка. Применить критерий согласия при уровне значимости равном 0,05;

2) Выписать плотность вероятности и функцию распределения этой случайной величины;

3) Найти вероятность того, что время бесперебойной работы станка будет не менее 35 часов;

4) Построить гистограмму и кривую распределения этой случайной величины;

Дано:

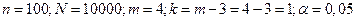
Время бесперебойной работы t α - β	кол-во станков ni	xi	xi *ni
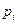
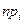
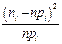
20-30				0,1	0,084	0,29
30-40				0,3	0,321	0,14
40-50				0,4	0,400	0,00
50-60				0,2	0,164	0,79
m = 4	n = 100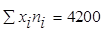

;

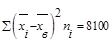
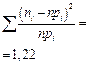
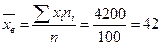
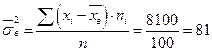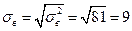
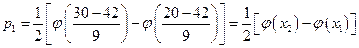
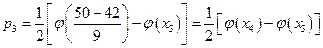
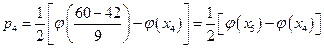
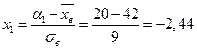
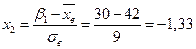
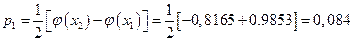
По таблице получено опытное значение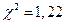

По таблице на странице 558 получено критическое значение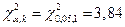

Опытное значение < 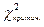, следовательно Н₀ не отвергается.

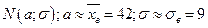
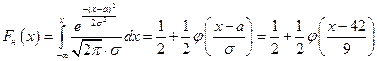
Неизвестные параметры α и σ приближенно равны их выборочным оценкам 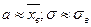. При достаточно большом объеме выборки в соответствии с законом больших чисел практически достоверно, что разница между оценкой и параметром сколь угодно мала.

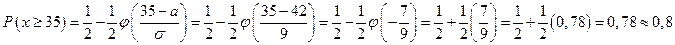
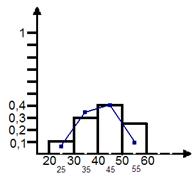
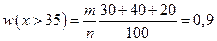
Расхождение между теоретическим и опытным значением связано с тем, что изучалась не вся совокупность, а лишь ее часть.

Замечание:

Расхождение между теоретическими и опытными данными неизбежно, т.к. рассматривается лишь часть генеральной совокупности, однако, если расхождение велико, то это заставляет предполагать, что теоретическая модель неадекватна реальности.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Математическая статистика

Вариационный ряд Х размер обуви х Х рост... Таблица... Можно также рассматривать частости для каждой варианты...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Критерий согласия Пирсона (критерий согласия (хи)).

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Вариационный ряд.
Пусть изучается признак Х, который может принимать значение х. Например: Х1 – размер обуви; х1 – 35; 36; Х2 – рост; х2

Среднее квадратическое отклонение вариационного ряда (аналог среднего квадратического отклонения случайной величины).
(3) Свойства числовых характеристик вариационного ряда аналогичны свойствам характери

Точечные оценки.
Характеристики генеральной совокупности называются неизвестными параметрами. Обозначение: θ (тэта). Определение: Оценкой неизвестного параметра θ называется случайная ве

Теоремы об оценках.
Теорема 1:Для повторной и бесповторной выборок при достаточно большом объеме выборки n выборочное среднее является случайной величиной распределенной по нормальному закону со следу

Требования к оценкам.
Пусть случайная величина Х является оценкой неизвестного параметра θ: 1. Оценка называется несмещенной, если математическое ожидание оценки совпадает с оцениваемыми параметрами, т.е.:

Средние квадратические ошибки.
Определение: Среднеквадратической ошибкой для выборочной средней называется среднеквадратическое отклонение выборочной средней. Обозначение: (15)

Интервальное оценивание.
Заменяя неизвестный параметр θ его оценкой Х, мы допускаем некоторую ошибку ∆, т.е. . ͧ

Доверительная вероятность при оценивании среднего значения.
Пусть требуется оценить неизвестное генеральное среднее, т.е. параметр . В соответствие с теоремой 3 его оценко

Доверительная вероятность при оценивании генеральной доли (вероятности).
Пусть требуется оценить неизвестный генеральный параметр. Р – генеральная доля (вероятность), т.е. в формуле 17 неизвестным параметром является θ. В качестве оценки Х берем выборочную долю w (

Критерии согласия.
В некоторых случаях нас интересует неизвестный закон распределения изученного признака Х во всей генеральной совокупности. В этом случае информация о законе распределения поступает с помощью выборк

Двумерная случайная величина.
Двумерной случайной величиной называется упорядоченная пара случайных величин . Каждое значение двумер

Условные математические ожидания.
Если построить условное распределение, т.е. ряд распределения одной случайной величины при фиксированном значении другой случайной величины, то можно для каждого из условных распределений посчитать

Виды зависимости между случайными величинами.
1. Функциональная – если каждому значению х соответствует единственное значение y. 2. Статистическая – если каждому значению х соответствует целый ряд распределения значения y (и наоборот)

Линейная регрессия.
Если уравнение регрессии является линейным, то говорят, что между x и y существует линейная корреляционная зависимость. Линейная корреляционная зависимость задается следующими уравнениями

Свойства коэффициента линейной корреляции.
1. r служит для определения тесноты линейной корреляционной зависимости; 2. r принимает значения от ;

Нахождение параметров линейных уравнений регрессии методом наименьших квадратов.
После того, как сделана выборка, в линейных уравнениях регрессии I и II условные математические ожидания заменяются их оценками – групповыми средними. Тогда уравнения регрессии принимают следующий

Свойства коэффициентов регрессии.
1. коэффициенты регрессии имеют одинаковый знак , совпадающий со знаком μ; 2. коэффициенты регрессии являются угловыми коэффициентами для соответствующих прямых I и II относительно с

Проверка значимости коэффициента корреляции.
Выдвигается гипотеза Н0, которая заключается в том, что между переменными х и y во всей генеральной совокупности не существует линейной корреляции не существует линейной корреляционной з