рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Прогнозування.

Реферат Курсовая Конспект

Выберите учебное заведение

Прогнозування.

Прогнозування. - раздел Математика, ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА Після Побудови Моделі (Теоретичної Регресійної Залежності) Та Перевірки Її Ад...

Після побудови моделі (теоретичної регресійної залежності) та перевірки її адекватності можна виконувати прогнозування. При цьому отримуємо точкові та інтервальні прогнози. Точковий прогноз дає оцінку значення залежної змінної, наприклад, для значення 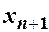за побудованою вибірковою моделлю:

При інтервальному оцінюванні застосовується -розподіл Стьюдента з 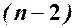ступенями вільності при заданому рівні значущості :

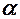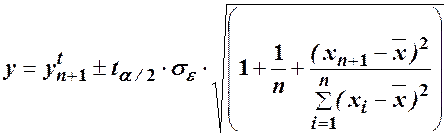де - середня квадратична помилка, 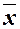- середнє значення фактора (регресора). Для нашого приклада (див.Додаток ) знайдено 95% довірчий інтервал прогнозованого випуску при збільшенні ОВФ до 70 млн.грн.

Економічна інтерпретація: коефіцієнт при змінній Х в моделі означає, що при збільшенні ОВФ на 1 млн.грн випуск зросте приблизно на 0,646 тон.

Класична модель лінійної регресії: основні припущення,

що лежать в основі методу найменших квадратів

Узагальнена лінійна регресійна модель

де - правильні параметри усієї генеральної сукупності, 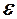- неспостережувана випадкова величина.

Мета регресійного аналізу полягає не тільки у визначенні невідомих параметрів вибіркової лінійної моделі , а, насамперед, у висновках, які ми можемо зробити щодо дійсних значень параметрів узагальненої моделі . Для того, щоб відповісти на запитання, наскільки наближаються знайдені оцінки до відповідних значень параметрів узагальненої моделі, або, що те ж саме, наскільки наближається теоретичне значення 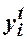до дійсного значення свого математичного сподівання 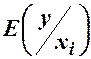, ми повинні не тільки точно визначити функціональну форму моделі, а й зробити певні припущення щодо випадкової величини (ВВ) 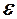та зв’язку між випадковою величиною та незалежною змінною .

Припущення 1. Математичне сподівання ВВ 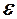дорівнює нулю:

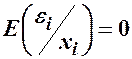Графічно:

Припущення 1 реально стверджує, що фактори, які не враховано в моделі і тому віднесено до , не впливають систематично на математичне сподівання , тобто додатні значення нейтралізують від’ємні , тому їхній усереднений чи очікуваний вплив на дорівнює нулю.

Зазначимо, що припущення 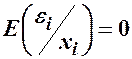еквівалентне умові .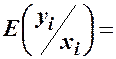

Припущення 2. Відсутність автокореляції між ВВ . Це припущення означає, що ВВ незалежні між собою, тобто коефіцієнт коваріації між ними дорівнює нулю:

На рисунках покажемо випадки відсутності автокореляції, а також наявність додатного та від’ємного зв’язку між ВВ:

Припущення 2 дає змогу розглянути найпростіший випадок, коли вивчається систематичний вплив (якщо він є) на 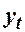без урахування впливу інших факторів, виражених ВВ 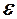. У супротивному випадку 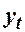залежатиме не тільки від , а й від 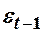. Тому потрібно тестувати наявність зв’язку між ВВ .

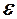Припущення 3. Гомоскедастичність, або однакова дисперсія ВВ незалежно від номера спостереження:

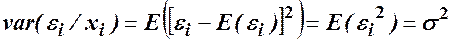Це припущення свідчить, що умовна дисперсія розподілу є також сталою величиною. Покажемо дану ситуацію, а також її порушення, тобто випадок гетероскедастичності на рисунках:

Припущення 4. Незалежність між значеннями і значеннями змінної , або нульова коваріація між ними:

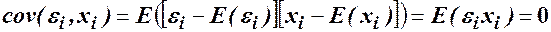Припущення 4 виконується автоматично, якщо змінна 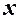є невипадковою, або нестохастичною (як у нашому прикладі ряду динаміки). Дане припущення суттєве у випадку, коли значення 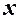випадкові.

Припущення 5. Регресійну модель визначено (специфіковано) правильно (відсутність похибки). Покажемо, що може бути у випадку порушення цього припущення на прикладі так званої кривої Філіпса:

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ... ОДЕСЬКИЙ ДЕРЖАВНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ... В М МАЦКУЛ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Прогнозування.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Одеса 2010
УДК 519.2 ББК 22.17я73 М 36 Рецензенти: С.В.Левинський –кандидат фізико-мат

Переставлення (перестановки).
Нехай потрібно підрахувати число способів, за якими можна розмістити в ряд

Приклади.
Властивості: 1.Для довільної події

Приклади.
Геометричне означення імовірності. Означення. Імовірність події

Приклади.
Статистичне означення імовірності. Означення.Нехай проводиться

ТеМА №2
1. Події залежні та незалежні. 2. Умовна імовірність. 3. Теорема добутку та наслідки з неї. 4. Теорема додаванн

ТЕМА №4
1. Незалежні повторні випробування (НПВ). 2. Формула Бернуллі. 3. Біноміальний закон розподілу (закон Бернуллі).

ТЕМА №5
1. Інтегральна функція розподілу та її властивості. 2. Диференціальна функція розподілу та її властивості. 3. Числові характеристики непе

Центральна гранична теорема.
4. Інтегральна теорема Муавра-Лапласа та її частинні випадки. Група теорем, які встановлюють відповідність між теоретичними та експериментальними характери

Система випадкових величин.
2. Закон розподілу двохвимірної ДВВ. 3. Функції розподілу двохвимірної ВВ. Залежність та незалежність ВВ. 4. Числові характеристики двохв

ТЕМА №8
1. Предмет математичної статистики. Статистичні сукупності (генеральна та вибіркова). 2. Способи відбору. Проста випадкова вибірка. Впорядкування даних та їх розпо

Приклади.
Часто необхідно знати закон розподілу ознаки у генеральній сукупності. Наприклад, є підстави вважати, що він має вигляд А. Тоді висувають гіпотезу (припущення): генеральна с

ТЕМА №10
1. Функціональна, статистична та кореляційна (регресійна) залежності. 2. Проста лінійна регресія. Основні положення. 3. О

ТЕМА №11
1. Множинний регресійний аналіз. Багатофакторна лінійна регресія. 2. Кореляційна матриця та її вибіркова оцінка. 3. Оцінка взаємозв’язку

Теорема добутку.
ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ. Приклад 1.1. Дана множина

Теореми добутку (продовження) та суми.
2. Повна імовірність. 3. Формула Байєса. ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ. Приклад 2.1. Два

ПРАКТИЧНЕ ЗАНЯТТЯ №3
1. Дискретні випадкові величини (ДВВ), їх закони розподілу. 2. Операції над ДВВ. 3. Числові характеристики ДВВ та їх властивості.

Локальна формула Лапласа, формула Пуассона.
15. Закон Пуассона (закон рідкісних подій). ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ. Приклад 4.1. В середньому 30% пакетів акцій продаються н

ПРАКТИЧНЕ ЗАНЯТТЯ №5
1. Функція розподілу імовірностей (інтегральна функція) та її властивості. 2. Щільність розподілу імовірностей (диференціальна функція) та її властивості.

Центральна гранична теорема.
4. Інтегральна теорема Муавра-Лапласа та її частинні випадки. ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ Приклад 6.1. Середня кі

ПРАКТИЧНЕ ЗАНЯТТЯ №8
1. Статистичні сукупності (генеральна та вибіркова), ознаки та їх розподіли. Числові характеристики статистичних розподілів. 2. Точкові та інтервальні оцінк

ПРАКТИЧНЕ ЗАНЯТТЯ №9
1. Статистичні гіпотези. Похибки перевірки гіпотез. 2. Критерії узгодження для перевірки гіпотез. Критична область та її знаходження. 3.

ПРАКТИЧНЕ ЗАНЯТТЯ №10
5. Функціональна, статистична та кореляційна (регресійна) залежності. 6. Проста лінійна регресія. Основні положення. 7. Оцінка щільності

ПРАКТИЧНЕ ЗАНЯТТЯ №11
1. Багатофакторна регресія. Основні положення. Особливості (відмінності від однофакторної). 2. Оцінка взаємозв’язку між змінними. Матриця коефіцієнтів парної корел