Линейные неравенства

Различают два типа линейных неравенств:

1) Строгие неравенства: .

2) Нестрогие неравенства: .

Какой геометрический смысл этих неравенств? Если линейное уравнение задаёт прямую, то линейное неравенство определяет полуплоскость.

Как известно, ось абсцисс задаётся уравнением y=0 – «игрек» всегда (при любом значении «икс») равняется нулю

Рассмотрим неравенство y >0 . Как его понимать неформально? «Игрек» всегда (при любом значении «икс») положителен. Очевидно, что данное неравенство определяет верхнюю полуплоскость – ведь там и находятся все точки с положительными «игреками».

В том случае, если неравенство нестрогое y >=0 , к верхней полуплоскости дополнительно добавляется сама ось Ox .

Аналогично: неравенству y <0 удовлетворяют все точки нижней полуплоскости, нестрогому y=<0 неравенству соответствует нижняя полуплоскость + ось Ox .

С осью ординат OY та же самая прозаичная история:

– неравенство x>0 задаёт правую полуплоскость; – неравенство x>=0 задаёт правую полуплоскость, включая ось ординат; – неравенство x<0 задаёт левую полуплоскость; – неравенство x=<0 задаёт левую полуплоскость, включая ось ординат.

На втором шаге рассмотрим неравенства, в которых отсутствует одна из переменных.

Отсутствует «игрек»: Ax+C >0 , Ax+C >=0, Ax+C <0, Ax+C =<0

Или отсутствует «икс»: By+C >0 , By+C >=0, By+C <0, By+C =<0

Решить линейное неравенство – это значит найти полуплоскость, точки которой удовлетворяют данному неравенству (плюс саму прямую, если неравенство нестрогое). Решение, как правило, графическое.

Правило: В неравенстве слагаемые переносятся из части в часть со сменой знака, при этом знак САМОГО неравенства не меняется (например, если был знак «меньше», то так и останется «меньше»).

Правило: Обе части неравенства можно умножить (разделить) на ПОЛОЖИТЕЛЬНОЕ число, при этом знак неравенства не меняется.

Решить систему линейных неравенств – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы.

В качестве простейших примеров рассмотрим системы неравенств, определяющих координатные четверти прямоугольной системы координат

Система неравенств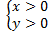 задаёт первую координатную четверть (правая верхняя).

Координаты любой точки первой четверти, например,(3;5),и т.д. удовлетворяют каждому неравенству данной системы.

Аналогично: – система неравенств 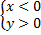задаёт вторую координатную четверть (левая верхняя); – система неравенств 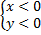задаёт третью координатную четверть (левая нижняя); – система неравенств задаёт четвёртую координатную четверть (правая нижняя).

Система линейных неравенств может не иметь решений, то есть, быть несовместной. Снова простейший пример: 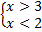. Совершенно очевидно, что «икс» не может одновременно быть больше трёх и меньше двух.

Решением системы неравенств может являться прямая, например:

Но самый распространённый случай, когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называется многоугольником решений системы.

Пример,

Решить систему линейных неравенств

На практике в большинстве случаев приходится иметь дело с нестрогими неравенствами, поэтому оставшуюся часть урока водить хороводы будут именно они.

Решение: то, что неравенств многовато, пугать не должно. Сколько может быть неравенств в системе? Да сколько угодно. Главное, придерживаться рационального алгоритма построения области решений:

1) Сначала разбираемся с простейшими неравенствами. Неравенства x>=0, y>=0 определяют первую координатную четверть, включая границу из координатных осей. Уже значительно легче, так как область поиска значительно сузилась. На чертеже сразу отмечаем стрелочками соответствующие полуплоскости (красные и синие стрелки)

2) 2) Второе по простоте неравенство – здесь отсутствует «игрек». Во-первых, строим саму прямую , а, во-вторых, после преобразования неравенства к виду x=<6 , сразу становится понятно, что все «иксы» меньше, чем 6. Отмечаем зелёными стрелками соответствующую полуплоскость. Ну что же, область поиска стала ещё меньше – такой не ограниченный сверху прямоугольник.

3) 3) На последнем шаге решаем неравенства «с полной амуницией»: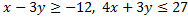. Алгоритм решения мы подробно рассмотрели в предыдущем параграфе. Вкратце: сначала строим прямую, потом с помощью подопытной точки находим нужную нам полуплоскость.

Область решений системы представляет собой многоугольник OABCD, на чертеже он обведён малиновой линией и заштрихован. Перестарался немного =) В тетради область решений достаточно либо заштриховать, либо жирнее обвести простым карандашом.

 

Любая точка данного многоугольника удовлетворяет КАЖДОМУ неравенству системы (для интереса можете проверить).

 

Ответ: решением системы является многоугольник OABCD .

 

52. Задача об оптимальном плане выпуска продукции

1. Построение задачи.

Предприятие выпускает n-видов продукции, используя для этого m- видов ограниченные ресурсов запасы, которых 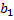, , 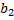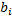(i=)

- количество ресурсов i - того вида.

I = - необходимо для изготовления одного изделия вида j.

Прибыль от реализации одного изделия вида j. Требуется определить сколько изделий нужно выпустить , чтобы суммарная прибыль от их реализации была максимальной.

Найти оптимальный план производства продукции по критерию максимума суммарной прибыли от реализации всех выпущенных изделий.

2. Построение математических моделей.

Пусть предприятие выпускает 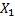,,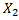 …. , 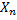изделий 1, 2, …,n-ого вида соответственно.

Количество изделий не может выражаться отрицательным числом

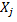>=0 (j=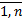) (1)

На изготовление одного изделия первого вида затрачивается единиц первого ресурса, а на изготовление 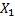изделий первого вида будет затрачено ресурсов первого вида.На изготовления изделий второго вида первый ресурс будет израсходован в количестве .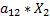

Всего первого ресурса будет израсходовано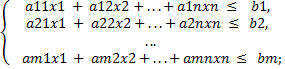

(2)

Суммарная прибыль от реализации всех изделий:

Z =+ =+ 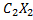... + =→ max

(1) И (2) —система ограничений задачи

(3)—целевая функция или критерий оптимальности.

Любая задача состоит из таких 2-х частей.

53. Общая задача линейного программирования (ЗЛП). ЗЛП в стандартной форме. Различные формы записи ЗЛП.

Общая постановка задачи линейного программирования (ЗЛП). Примеры ЗЛП

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Несколько слов о самом термине линейное программирование. Он требует правильного понимания. В данном случае программирование - это, конечно, не составление программ для ЭВМ. Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:

задача об оптимальном использовании ресурсов при производственном планировании;

задача о смесях (планирование состава продукции);

задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");

транспортные задачи (анализ размещения предприятия, перемещение грузов).

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим:

математические модели большого числа экономических задач линейны относительно искомых переменных;

данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;

многие задачи линейного программирования, будучи решенными, нашли широкое применение;

некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

целевая функция Z =+ =+ 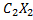... + =→max(min); (2.1)

 

ограничения:

(2.2)

 

требование неотрицательности: Xj ≥ 0, (2.3)

При этом aij, bi, cj (i=, j=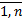) - заданные постоянные величины.

Задача состоит в нахождении оптимального значения функции (2.1) при соблюдении ограничений (2.2) и (2.3).

Систему ограничений (2.2) называют функциональными ограничениями задачи, а ограничения (2.3) - прямыми.

Вектор 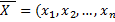) , удовлетворяющий ограничениям (2.2) и (2.3), называется допустимым решением (планом) задачи линейного программирования. План 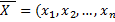) , при котором функция (2.1) достигает своего максимального (минимального) значения, называется оптимальным.

Далее приведем примеры некоторых типовых задач, решаемых при помощи методов линейного программирования. Такие задачи имеют реальное экономическое содержание. Сейчас лишь сформулируем их в терминах ЗЛП, а методы решения подобных задач рассмотрим ниже.

1. Задача об оптимальном использовании ресурсов при производственном планировании.

Общий смысл задач этого класса сводится к следующему.

Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b1, b2,..., bm условных единиц.

Известны также технологические коэффициенты aij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида (i=, j=).

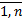Прибыль, получаемая предприятием при реализации изделия j-го вида, равна cj.

В планируемом периоде значения величин aij, bi и cj остаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.