АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

1. Плоскости α и β пересекают вспомогательной плоскостью γ.

2. Строят линии пересечения вспомогательной плоскости с заданными α и β. Это линии 1-2 и 3-4.

3. Отмечают точку пересечения построенных линий 1-2 ∩ 3-4 = М.

 

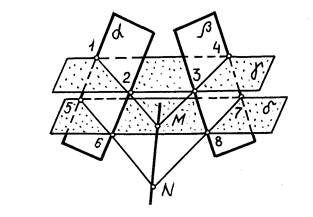
Рис.6

Для построения второй точки N алгоритм решения повторяют.

Пример. Построить проекции линии пересечения двух плоскостей общего положения.

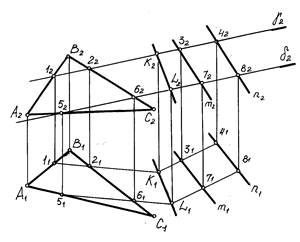Рис.7

 

Как видно из рис.7 одна из плоскостей α задана треугольником α(АВС), а вторая β – параллельными прямыми (m ║ n). Для решения задачи обе плоскости пересечены вспомогательными проецирующими плоскостями γ₂ и δ₂.

(В качестве вспомогательных плоскостей можно было провести плоскости уровня). Плоскость γ пересекает плоскость α(АВС) по линии 1-2, а плоскость β(m ║ n) - по линии 3-4. В пересечении этих линий определена точка K, общая для двух плоскостей.

Аналогично пересекая заданные плоскости второй вспомогательной плоскостью δ, можно найти вторую точку L общую обеим плоскостям.

Следует заметить, что если вспомогательные плоскости γ и δ параллельны, то и линия пересечения 1-2 параллельна 5-6, а линия 3-4 параллельна линии 7-8.

Прямая, проходящая через точки K и L, определяет искомую линию пересечения плоскостей α и β.

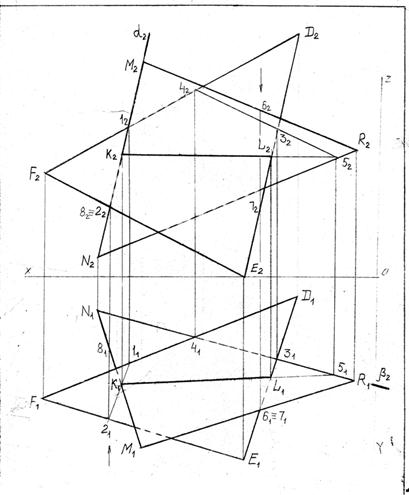
В работе №1 студенты строят линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты

 

вершин которых заданы в таблице исходных данных.

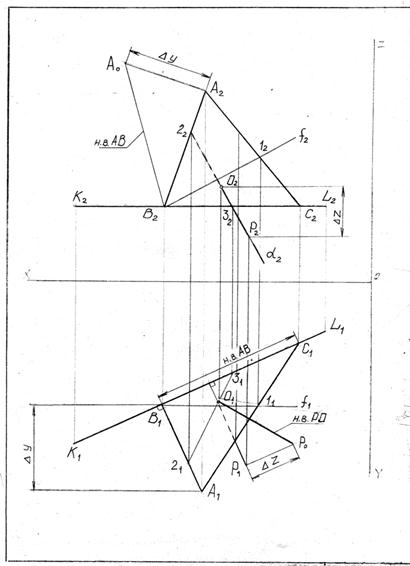
Решение задачи можно упростить (рис.8) если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.

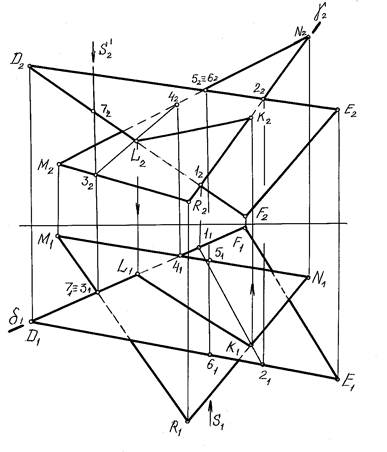
Рис. 8

Так точка K этой линии определена с помощью фронтальнопроецирущей плоскости γ₂, проведенной через сторону RN треугольника MNR. Именно линия RN является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью γ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.

Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной γ), находится в пересечении прямых 1-2 и RN.

Следует отметить, что если вспомогательная плоскость γ фронтальнопроецирущая, то сначала определяется горизонтальная проекция точки K₁, т.е. K₁ = 1₁-2₁∩R₁N₁, а затем по линии проекционной связи находится K₂ – фронтальная проекция точки K.

Аналогично, заключая сторону DF в горизонтальнопроецирующую плоскость δ₁, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Например, определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции (см рис.8). Для этого проведем луч зрения s перпендикулярно П₂ через точку пересечения фронтальных проекций D₂E₂ и M₂N₂. В пересечении D₂E₂ и M₂N₂ расположены две конкурирующие по видимости точки (5₂ и 6₂). Точка 5 принадлежит стороне MN, а точка 6 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D₁E₁ в точке 6₁, а затем M₁N₁ в точке 5₁. Следовательно, фронтальная проекция D₂E₂ – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П₁ через две конкурирующие на П₁ точки скрещивающихся прямых (например, луч s^/, проходящий через точки 3 и 7, соответственно принадлежащие прямым MR и DF).

 

ЗАДАЧА№3

Определить натуральную величину расстояния от точки Р до плоскости.

 

Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.

Для решения задачи необходимо:

1. Из заданной точки Р опустить перпендикуляр на плоскость α.

2. Определить точку пересечения (точка К) перпендикуляра с плоскостью.

3. Определить натуральную величину перпендикуляра.

Рассмотрим более подробно каждый пункт приведенного выше алгоритма.

Пример 1. Из точки Р опустить перпендикуляр n на плоскость α(a∩b)

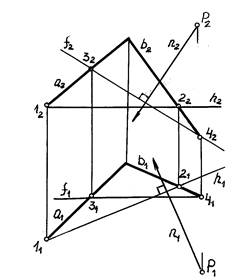(рис.9)

Рис.9

На основании теоремы о перпендикуляре к плоскости горизонтальная проекция n₁ перпендикуляра n проводится перпендикулярно к горизонтальной проекции горизонтали h. Не- зависимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости α(a∩b) проведена произвольная фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.

 

Пример 2. Построить точку пересечения прямой n с плоскостью α. Пространственное решение задачи на рис.10.

 

 

Рис.10

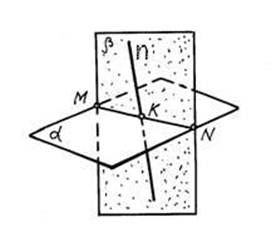
Задача решается в три этапа:

1. Данная прямая n заключается во вспомогательную плоскость β

n € β

Построения будут простейшими, если β будет проецирующей;

2. Строится линия пересечения MN вспомогательной плоскости β с заданной α

β∩α=MN;

3. В пересечении полученной линии MN с заданной n находится искомая точка K

MN∩n=K

Пример 3. Определить точку К пересечения перпендикуляра n с плоскостью α(h∩ƒ) и натуральную величину перпендикуляра (рис.11).

 

Прямая n заключена во фронтальнопроецирующую плоскость β, n € β. Затем определена линия пересечения 1-2 вспомогательной плоскости β с заданной плоскостью α(h∩ƒ), 1-2=β∩α.

В пересечении линии 1-2 с прямой n найдена искомая точка К. Сначала определяется горизонтальная проекция К₁(К₁=1₁-2₁∩n₁), а затем по линии проекционной связи определена ее фронтальная К₂ проекция.

 

Натуральная величина перпендикуляра определена способом прямоугольного треугольника.

Исходными данными для решения задачи 3 являются точка Р, заданная координатами и плоскость треугольника АВС, проекции которого построены в задаче № 1.

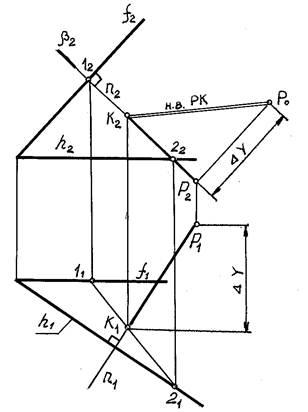
Рис.11

 

Рис.12

 

 

 

Список литературы

 

1. Крылов Н.Н., Начертательная геометрия – М.: Высшая школа, 2005г.

2. Четверухин Н.Ф., Начертательная геометрия – М.: Высшая школа, 1963г.

3. Кузнецов Н.С., Начертательная геометрия – М.: Высшая школа, 1982г.

 

Учебно-методическое издание

 

Горбачева Нина Петровна

Начертательная геометрия

Методические указания к

выполнению работы №1

 

 

Подписано в печать- Формат 60х84/16 Тираж 300

 

Усл.- печ. л. 1,5 Изд. № Заказ №

127994, Москва, ул. Образцова, 15. Типография МИИТа