Поток тепла; точечный источник вблизи бесконечной плоской границы - Лекция, раздел Физика, Фейнмановские лекции по физике Ранее Мы Уже Обсуждали (Гл. 3, § 4) Поток Тепла. Вообразите Кусок Какого-То М...
Ранее мы уже обсуждали (гл. 3, § 4) поток тепла. Вообразите кусок какого-то материала, необязательно однородного (в разных местах может быть разное вещество), в котором температура меняется от точки к точке. Как следствие этих температурных изменений возникает поток тепла, который можно обозначить вектором h. Он представляет собой количество тепловой энергии, которое проходит в единицу времени через единичную площадку, перпендикулярную потоку. Дивергенция h есть скорость ухода тепла из данного места в расчете на единицу объема:
Ñ•h = Скорость ухода тепла на единицу объема.
(Мы могли, конечно, записать уравнение в интегральном виде, как мы поступали в электродинамике с законом Гаусса, тогда оно выражало бы тот факт, что поток через поверхность равен скорости изменения тепловой энергии внутри материала. Мы не будем больше переводить уравнения из дифференциальной формы в интегральную и обратно, это делается точно так же, как в электростатике.)
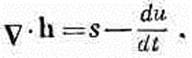
Скорость, с которой тепло поглощается или рождается в разных местах, конечно, зависит от условий задачи. Предположим, например, что источник тепла находится внутри материала (возможно, радиоактивный источник или сопротивление, через которое пропускают ток). Обозначим через s тепловую энергию, производимую этим источником в единице объема за 1 сек. Кроме того, могут возникнуть потери (или, наоборот, дополнительное рождение) тепловой энергии за счет перехода в другие виды внутренней энергии в данном объеме. Если и — внутренняя энергия в единице объема, то —du/dt будет тоже играть роль «источника» тепловой энергии. Итак, имеем
(12.5)
Мы не собираемся здесь обсуждать полное уравнение, величины в котором изменяются со временем, потому что мы проводим аналогию с электростатикой, где ничто не зависит от времени. Мы рассмотрим только задачи с постоянным потоком тепла, в которых постоянные источники создают состояние равновесия. В таких случаях

(12.6)
Нужно иметь, конечно, еще одно уравнение, которое описывает, как поток течет в разных местах. Во многих веществах поток тепла примерно пропорционален скорости изменения температуры с положением: чем больше разность температур, тем больше поток тепла. Мы знаем, что вектор потока тепла пропорционален градиенту температуры. Константа пропорциональности К, зависящая от свойств материала, называется коэффициентом теплопроводности
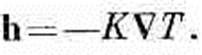
(12.7)
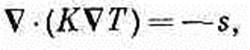
Если свойства материала меняются от точки к точке, то К=К (х, у, z) и есть функция положения. [Уравнение (12.7) не столь фундаментально, как (12.5), выражающее сохранение тепловой энергии, потому что оно зависит от характерных свойств вещества.] Подставляя теперь уравнение (12.7) в (12.6), получаем
(12.8)
что в точности совпадает по форме с (12.4). Задачи с постоянным потоком тепла и задачи электростатики одинаковы. Вектор потока тепла h соответствует Е, а температура Т соответствует j.
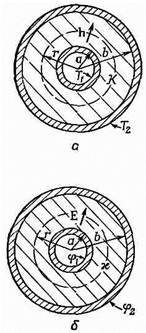
Фиг. 12.1. Поток тепла в случае цилиндрической симметрии (а) и соответствующая задача из электричества (б).
Мы уже отмечали, что точечный тепловой источник создает поле температур, меняющееся, как 1/r, и поток тепла, меняющийся, как 1/r2. Это есть не более чем простой перенос утверждений электростатики, что точечный заряд дает потенциал, меняющийся, как 1/r, и электрическое поле, меняющееся, как 1/r2. Вообще мы можем решать статистические тепловые задачи с той же степенью легкости, как и задачи электростатики.
Рассмотрим простой пример. Пусть имеется цилиндр с радиусом а при температуре T1? поддерживающейся за счет генерации тепла в цилиндре. (Это может быть, скажем, проволока, по которой течет ток, или трубка с конденсацией пара внутри цилиндра.) Цилиндр покрыт концентрической обшивкой из изолирующего материала с теплопроводностью К. Пусть внешний радиус изоляции равен b, а в наружном пространстве поддерживается температура T2 (фиг. 12. 1, а). Нам нужно определить скорость потери тепла проволокой или паропроводом (все равно чем), проходящим по центру цилиндра. Пусть полное количество тепла, теряемого на длине трубы L, равно G, его-то мы и хотим найти.
Как надо решать такую задачу? У нас есть дифференциальные уравнения, но поскольку они такие же, как в электростатике, то математическое решение их нам уже известно. Аналогичная задача электростатики относится к проводнику радиусом а при потенциале j1, отделенном от другого проводника радиусом b при потенциале j2, с концентрическим слоем диэлектрика между ними (фиг. 12.1, б). Далее, поскольку поток тепла h соответствует электрическому полю Е, то наша искомая величина G соответствует потоку электрического поля от единичной длины (другими словами, электрическому заряду на единице длины, деленному на e0). Мы решали электростатическую задачу с помощью закона Гаусса. Нашу задачу о потоке тепла будем решать таким же способом.
Из симметрии задачи мы видим, что h зависит только от расстояния до центра. Поэтому мы окружим трубку гауссовой поверхностью — цилиндром длиной L и радиусом r. С помощью закона Гаусса мы выводим, что поток тепла h, умноженный на площадь поверхности 2prL, должен быть равен полному количеству тепла, рождаемому внутри, т. е. тому, что мы назвали G:

(12.9)
Поток тепла пропорционален градиенту температуры
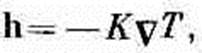
или в данном случае величина h равна
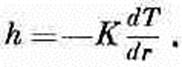
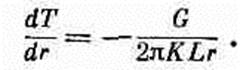
Вместе с (12.9) это дает
(12.10)

Интегрируя от r=а до r=b, получаем
(12.11)
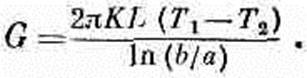
Разрешая отнсительно G, находим
(12.12)
Этот результат в точности соответствует формуле для заряда цилиндрического конденсатора:
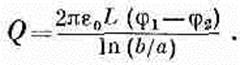
Задачи одинаковые и имеют одинаковые решения. Зная электростатику, мы тем самым знаем, сколько тепла теряет изолированная труба.
Рассмотрим еще один пример. Пусть мы хотим узнать поток тепла в окрестности точечного источника, расположенного неглубоко под поверхностью земли или же вблизи поверхности большого металлического предмета. В качестве локализованного источника тепла может быть и атомная бомба, которая взорвалась под землей и представляет собой мощный источник тепла, или же небольшой источник радиоактивности внутри железного блока — возможностей очень много.
Рассмотрим идеализированную задачу о точечном источнике тепла, мощность которого G, на расстоянии а под поверхностью бесконечной однородной среды с коэффициентом теплопроводности К. Теплопроводностью воздуха над поверхностью среды мы пренебрежем. Мы хотим определить распределение температуры на поверхности среды. Насколько горячо будет прямо над источником и в разных местах на поверхности?
Как же решить эту задачу? Она похожа на задачу по электростатике, в которой имеются два материала с разной диэлектрической проницаемостью x по обе стороны от разделяющей их границы. Здесь что-то есть! Возможно, это похоже на точечный заряд вблизи границы между диэлектриком и проводником или что-нибудь вроде этого. Посмотрим, что происходит вблизи границы. Физическое условие состоит в том, что нормальная составляющая h на поверхности равна нулю, поскольку мы предположили, что потока из блока нет. Мы должны задать вопрос: в какой электростатической задаче возникает условие, что нормальная компонента электрического поля Е (представляющая собой аналог h) равна нулю у поверхности? Нет такой!
Это один из тех случаев, к которым следует относиться с осторожностью. По физическим причинам могут быть определенные ограничения тех математических условий, которые возникают в каком-либо случае. Поэтому если мы проанализировали дифференциальное уравнение только для некоторых ограниченных примеров, то вполне можем упустить ряд решений, возникающих в других физических условиях. Например, нет материала, обладающего диэлектрической проницаемостью, равной нулю, а теплопроводность вакуума равна нулю. Поэтому нет электростатического аналога идеального теплоизолятора. Мы можем, однако, попытаться использовать те же методы. Попробуем вообразить, что произошло бы, если бы диэлектрическая проницаемость была равна нулю. (Разумеется, в реальных условиях диэлектрическая проницаемость никогда не обращается в нуль. Но может представиться случай, когда вещество имеет очень большую диэлектрическую проницаемость, так что диэлектрической проницаемостью воздуха вне среды можно пренебречь.)
Как же найти электрическое поле, у которого нет составляющей, перпендикулярной к поверхности? Иначе говоря, такое поле, которое всюду касательно к поверхности? Вы заметите, что эта задача обратна задаче о точечном заряде вблизи проводящей плоскости. Там нам нужно было поле, перпендикулярное
к поверхности, потому что проводник всюду находился при одном и том же значении потенциала.
В задаче об электрическом поле мы придумали решение, вообразив за проводящей плоскостью точечный заряд. Можно воспользоваться снова этой же идеей. Попытаемся выбрать такое «изображение» источника, которое автоматически обращало бы в нуль нормальную компоненту поля вблизи поверхности. Решение показано на фиг. 12.2. Электрическое изображение источника с тем же знаком и той же величины, находящееся на расстоянии а над поверхностью, дает поле, горизонтальное повсюду у поверхности. Нормальные компоненты от обоих источников взаимно уничтожаются.
Итак, наша задача о потоке тепла решена. Температура во всем пространстве одинакова по непосредственной аналогии с потенциалом от двух одинаковых точечных зарядов. Температура Т на расстоянии r от одного точечного источника G в бесконечной среде равна
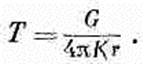
(12.13)

(Это, конечно, полностью аналогично j= q/4pe0r.) Температура точечного источника и, кроме того, его изображения равна
(12.14)
Эта формула дает нам температуру всюду внутри блока. Несколько изотермических поверхностей приведено на фиг. 12.2.
Показаны также линии h, которые можно получить из выражения h =-КÑТ.
В самом начале мы интересовались распределением температуры на поверхности. Для точки на поверхности находящейся на расстоянии р от оси, r1=r2=Ö (р2 + а2),

Фиг. 12.2. Поток тепла и изотерма у точечного источника тепла, расположенного на расстоянии а под поверхностью тела с хорошей теплопроводностью. Вне тела показано мнимое изображение источника.
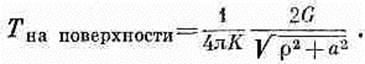
следовательно,
(12.15)
Эта функция также изображена на фиг. 12.2. Естественно, что температура прямо над источником выше, чем вдали от него. Такого рода задачи часто приходится решать геофизикам. Теперь мы видим, что это те же самые задачи, которые мы решали в электричестве.
Все темы данного раздела:
Электрические силы
Рассмотрим силу, которая, подобно тяготению, меняется обратно квадрату расстояния, но только в миллион биллионов биллионов биллионов раз более сильную. И которая отличается еще в одном. Пу
Электрические и магнитные поля
Первым делом нужно несколько расширить наши представления об электрическом и магнитном векторах Е и В. Мы определили их через силы, действующие на заряд. Теперь мы намереваемся говорить об элект
Характеристики векторных полей
Векторные поля обладают двумя математически важными свойствами, которыми мы будем пользоваться при описании законов электричества с полевой точки зрения. Представим себе замкнутую поверхность и зад
Законы электромагнетизма
Первый закон электромагнетизма описывает поток электрического поля:
Что это такое — «поля»?
Сделаем теперь несколько замечаний о принятом нами способе рассмотрения этого вопроса. Вы можете сказать: «Все эти потоки и циркуляции чересчур абстрактны. Пусть в каждой точке пространства есть э
Электромагнетизм в науке и технике
В заключение мне хочется закончить эту главу следующим рассказом. Среди многих явлений, изучавшихся древними греками, были два очень странных. Первое: натертый кусочек янтаря мог поднять маленьки
Понимание физики
Физик должен обладать умением подходить к задаче с разных точек зрения. Точный анализ реальных физических проблем обычно крайне сложен, и любое конкретное физическое явление может оказаться слишко
Скалярные и векторные поля — Т и h
Мы начинаем сейчас рассмотрение абстрактного, математического подхода к теории электричества и магнетизма. Наша цель — объяснить смысл законов, написанных в гл. 1. Но для этого надо сперва объясни
Производные полей — градиент
Когда поля меняются со временем, то их изменение можно описать, задав их производные по t. Мы хотим также описать и их изменение в пространстве, потому что мы интересуемся связью, скажем, ме
Выбрав удобную систему координат, мы можем написать
Т1 = Т(х, у, z) и Т2=Т(х + Dх, у + Dу, z + Dz),
где Dx:, Dy, Dz — компоненты вектора DR (фиг. 2.5). Вспомнив (2.7), напишем
Дифференциальное уравнение потока тепла
Приведем другой пример векторной записи физического закона. Этот закон не из точных, но во многих металлах и других материалах, проводящих тепло, он проявляется совершенно четко. Известно, что есл
Если площадь этой плиты DА, то поток тепла за единицу времени равен
(2.42)
Коэффициент пропорциональности c (каппа) называется теплопроводностью.
Вторые производные векторных полей
Пока мы имели дело только с первыми производными. А почему не со вторыми? Из вторых производных можно составить несколько комбинаций:
Криволинейный интеграл от Ñψ
В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено довольно много, все их можно подытожи
Поток векторного поля
Прежде чем рассматривать следующую интегральную теорему — теорему о дивергенции,— хотелось бы разобраться в одной идее, смысл которой в случае теплового потока легко усваивается. Мы уже определи
Поток из куба; теорема Гаусса
Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, сут
Теплопроводность; уравнение диффузии
Чтобы привыкнуть к теореме, разберем на примере, как ее применяют. Обратимся опять к распространению тепла, скажем в металле, рассмотрим совсем простой случай: все тепло было подведено к телу заран
Циркуляция векторного поля
Мы хотим теперь рассмотреть ротор поля примерно так же, как рассматривали дивергенцию. Мы вывели теорему Гаусса, вычисляя интеграл по поверхности, хотя с самого начала отнюдь не было ясно, что мы б
Циркуляция по квадрату; теорема Стокса
Как нам найти циркуляцию по каждому квадратику? Все зависит от того, как квадрат ориентирован в пространстве. Если ориентация его подобрана удачно (к примеру, он расположен в одной из координатных
Поля без роторов и поля без дивергенций
Теперь перейдем к некоторым следствиям из наших новых теорем. Возьмем сперва случай вектора, у которого ротор (или вихрь) повсюду равен нулю. Тогда, согласно теореме Стокса, циркуляция по лю
Статика
Начнем теперь подробное изучение теории электромагнетизма. Она вся (весь электромагнетизм целиком) запрятана в уравнениях Максвелла:
Магнитостатика
Обратите внима
Закон Кулона
(4.9)
Электрический потенциал
Для начала усвоим понятие электрического потенциала, связа
Электростатический потенциал
(4.22)
Часто очень удобно брать
Поток поля Е
Теперь мы хотим вывести уравнение, которое непосредственно и в лоб учитывает тот факт, что закон силы — это закон обратных квадратов. Кое-кому кажется «вполне естественным», что поле меняется обра
Закон Гаусса; дивергенция поля Е
Наш изящный результат — уравнение (4.32) — был доказан для отдельного точечного заряда. А теперь допустим, что имеются два заряда: заряд ql—в одной точке и заряд (q2 —
Поле заряженного шара
Одной из самых трудных задач, которую пришлось нам решать, когда мы изучали теорию гравитационного притяжения, было доказать, что сила, создаваемая твердым шаром на его поверхности, такая же, как
Линии поля; эквипотенциальные поверхности
Теперь мы собираемся дать геометрическое описание электростатического поля. Два закона электростатики: один — о пропорциональности потока и внутреннего заряда и другой — о том, что электрическое
Электростатика—это есть закон Гаусса плюс...
Существуют два закона электростатики: поток электрического поля из объема пропорционален заряду внутри него — закон Гаусса, и циркуляция электрического поля равна нулю — Е есть градиент. Из этих д
Равновесие в электростатическом поле
Рассмотрим сначала следующий вопрос: в каких условиях точе
Равновесие с проводниками
В системе закрепленных зарядов устойчивого места для пробного заряда нет. А как обстоит дело с системой заряженных проводников? Может ли система заряженных проводников создать поле, в котором для
Устойчивость атомов
Раз заряды не могут иметь устойчивого положения, то, разумеется, неправильно представлять вещество построенным из статических точечных зарядов (электронов и протонов), управляемых только
Поле заряженной прямой линии
Закон Гаусса может быть применен для решения множества задач, связанных с электрическим полем, обладающим специальной симметрией (чаще всего сферической, цилиндрической или плоской). В оставшейся
Заряженная плоскость; пара плоскостей
В качестве другого примера рассчитаем поле однородно заряженного плоского листа. Предположим, что лист имеет бесконечную протяженность и заряд на единицу площади равен а. Сразу приходит в голову сл
Однородно заряженный шар; заряженная сфера
В гл. 4 мы уже применяли закон Гаусса, когда должны были найти поле вне однородно заряженной шаровой области. Тот же метод может дать нам и поле в точках внутри шара. Этот расчет, например,
Точен ли закон Кулона?
Если мы вглядимся чуть пристальнее в то, как поле в
Поля проводника
Проводник электричества — это твердое тело, в котором есть много «свободных» электронов. Электроны могут двигаться в веществе свободно, но не могут покидать поверхности. В металле бывает та
Поле внутри полости проводника
Вернемся теперь к проблеме пустотелого резервуара — проводника, имеющего внутри полость. В металле поля нет, а вот есть ли оно в полости? Покажем, что если полость пуста, то п
Уравнения электростатического потенциала
В этой главе мы расскажем о поведении электрического поля в тех или иных обстоятельствах. Вы познакомитесь с тем, как ведет себя электрическое поле, и с некоторыми математическими методами, испол
Электрический диполь
Сначала возьмем два точечных заряда +q и -q,
Замечания о векторных уравнениях
Здесь, пожалуй, уместно сделать общее замечание, касающееся векторного анализа. Хотя его теоремы и доказаны в общем виде, однако, приступая к расчетам и анализу какой-либо задачи, следует с толко
Диполъный потенциал как градиент
Мы хотели бы теперь отметить любопытное свойство формулы д
Дипольное приближение для произвольного распределения
Столь же интересно и не менее важно поле диполя, возникающее при других обстоятельствах. Пусть у нас есть тело со сложным распределением заряда, скажем, как у молекулы воды (см. фиг. 6.2), а нас и
Поля заряженных проводников
Мы покончим на этом с примерами таких физических задач, в которых распределение зарядов известно с самого начала. Такие задачи решаются без особых затруднений, в худшем случае требуя нескольких ин
Метод изображений
Мы определили поле двух точечных зарядов. На фиг. 6.8 показаны некоторые линии поля и эквипотенциальные поверхности, полученные из расчетов, приведенных в гл. 5. Рассмотрим теперь эквипотенциальн
Точечный заряд у проводящей плоскости
В качестве простейшего применения этого метода используем плоскую эквипотенциальную поверхность В (см. фиг. 6.8). Она поможет нам решить задачу о заряде вблизи проводящей плоскости. Для этог
Точечный заряд у проводящей сферы
А какие еще поверхности, кроме плоскости, имеют простое решение? Самая простая из них — сфера. Попробуем определить поля вокруг металлической сферы с точечным зарядом q вблизи нее (фиг. 6.11
Конденсаторы; параллельные пластины
Теперь обратимся к другому роду задач, связанных с проводниками. Рассмотрим две широкие металлические пластины, параллельные между собой и разделенные узким (по сравнению с их размерами) промежутк
Пробой при высоком напряжении
Сейчас мы качественным образом рассмотрим некоторые характеристики полей вокруг проводников. Зарядим электричеством проводник, но на сей раз не сферический, а такой, у которого есть острие или р
Ионный микроскоп
Сверхвысокое электрическое поле, окружающее всякий острый выступ заряженного проводника, получило интересное применение в одном приборе. Работа ионного микроскопа обусловлена мощными полями
Методы определения электростатического поля
В этой главе мы продолжим рассмотрение характеристик электрических полей в различных условиях. Сперва мы опишем один из наиболее разработанных методов расчета полей в присутствии проводников. Мы
Двумерные поля; функции комплексного переменного
Комплексная величина з определяется так:
Колебания плазмы
Займемся теперь такими физическими задачами, в которых поле создается не закрепленными зарядами и не зарядами на проводящих поверхностях, а сочетанием обоих факторов. Иными словами, полем управляю
Коллоидные частицы в электролите
Обратимся к другому явлению, когда местоположение зарядов определяется потенциалом, создаваемым в какой-то степени самими зарядами. Такой эффект существен для поведения коллоидов. Коллоид — это вз
Электростатическое поле сетки
Напоследок мы хотим изложить еще одно интересное свойство электрических полей. Оно используется в электрических приборах, электронных лампах и для других целей. Речь идет о поведении электрическог
Электростатическая энергия зарядов. Однородный шар
Одно из самых интересных и полезных открытий в механике —это закон сохранения энергии. Зная формулы для кинетической и потенциальной энергий механической системы, мы способны обнаруживать связь
Энергия конденсатора. Силы, действующие на заряженные проводники
Рассмотрим теперь энергию, требуемую на то, чтоб зарядить конденсатор. Если заряд Q был снят с одной обкладки конденсатора и перенесен на другую, то между обкладками возникает разность поте
Электростатическая энергия ионного кристалла
Рассмотрим теперь применение понятия электростатической энергии в атомной физике. Мы не можем запросто измерять силы, действующие между атомами, но часто нас интересует разница в энергиях двух расс
Электростатическая энергия ядра
Обратимся теперь к другому примеру электростатической энергии в атомной физике — к электростатической энергии атомного ядра. Прежде чем заняться этим вопросом, мы должны рассмотреть некоторые свойс
Энергия в электростатическом поле
Рассмотрим теперь другие способы подсчета электростатической энергии. Все они могут быть получены из основного соотношения (8.3) суммированием (по всем парам) взаимных энергий каждой пары зарядов
Энергия точечного заряда
Новое соотношение (8.35) говорит нам, что даже у отдельного точечного заряда q имеется какая-то электростатическая энергия. Поле в этом случае дается выражением
Градиент электрического потенциала в атмосфере
В обычный день над пустынной равниной или над морем электрический потенциал по мере подъема возрастает с каждым метром примерно на 100 в. В воздухе имеется вертикальное электрическое поле Е
Электрические токи в атмосфере
Помимо градиента потенциала, можно измерять и другую величину — ток в атмосфере. Плотность его мала: через каждый квадратный метр, параллельный земной поверхности, проходит около 10-6
Происхождение токов в атмосфере
Теперь нужно ответить на вопрос об источнике больших отрицательных токов, которые должны течь от «верха» к земной поверхности, чтобы поддержать ее отрицательный заряд. Где же те батареи, которые эт
Механизм распределения зарядов
Теперь мы хотим обратиться к обсуждению самой важной для нас стороны дела — к возникновению электрических зарядов. Разного рода эксперименты, включая полеты сквозь грозовой фронт (пилоты, соверша
Диэлектрическая проницаемость
Сейчас мы разберем еще одно характерное свойство материи, возникающее под влиянием электрического поля. В одной из предыдущих глав мы рассмотрели поведение проводников, в которых заряды под
Вектор поляризации Р
Продолжив наш анализ, мы обнаружим, что идея о проводящих и непроводящих участках не так уж существенна. Любой из маленьких шариков действует как диполь, момент которого создается внешним полем. Д
Поляризационные заряды
Посмотрим теперь, что дает эта модель для конденсатора с диэлектриком. Рассмотрим сначала лист материала, в котором на единицу объема приходится дипольный момент Р. Получится ли в результате в сре
Уравнения электростатики для диэлектриков
Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид
Поля и силы в присутствии диэлектриков
Мы докажем сейчас ряд довольно общих теорем электростатики для тех случаев, когда имеются диэлектрики. Мы уже видели, что емкость плоского конденсатора при заполнении его диэлектриком увеличиваетс
Молекулярные диполи
В этой главе мы поговорим о том, почему вещество бывает д
Электронная поляризация
Займемся сначала поляризацией неполярных молекул. Начнем с простейшего случая одноатомного газа (например, гелия). Когда атом такого газа находится в электрическом поле, электроны его тянутся в одн
Полярные молекулы; ориентационная поляризация
Теперь рассмотрим молекулу, обладающую постоянным дипольным моментом р0 , например молекулу воды. В отсутствие электрического поля отдельные диполи смотрят в разных направлениях,
Электрические поля в пустотах диэлектрика
Теперь мы переходим к интересному, но сложному вопросу о диэлектрической проницаемости плотных веществ. Возьмем, например, жидкий гелий, или жидкий аргон, или еще какое-нибудь неполярное вещество.
Следовательно, если поле внутри однородного диэлектрика мы назовем Е, то можно записать
E=Eдырка+Eшарнк,
(11.23)
где Eдырка — поле в дырке, а Eшарик — поле в однородно поляризованном шарике (фиг. 11.6). Поле однородно
Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти
В жидкости мы ожидаем, что поле, поляризующее отдельный атом, скорее похоже на Едырка, чем просто на Е. Если взять Eдырка из (11.25) в качестве поляризующего поля, входящего
Твердые диэлектрики
Обратимся теперь к твердым телам. Первый интересный факт относительно твердых тел заключается в том, что у них бывает постоянная поляризация, которая существует даже и без приложения внешнего элект
Сегиетоэлектричество; титанат бария
Мы опишем здесь особый класс кристаллов, которые, можно сказать, почти случайно обладают «встроенным» постоянным электрическим моментом. Ситуация здесь настолько критична, что, если слегка увеличит
Одинаковые уравнения — одинаковые решения
Вся информация о физическом мире, приобретенная со времени зарождения научного прогресса, поистине огромна, и кажется почти невероятным, чтобы кто-то овладел заметной частью ее. Но фактически физи
Натянутая мембрана
Рассмотрим теперь совсем другую область физики, в которой тем не менее мы придем снова к точно таким же уравнениям. Возьмем тонкую резиновую пленку — мембрану, натянутую на большую горизонтальную р
Диффузия нейтронов; сферически-симметричный источник в однородной среде
Приведем еще один пример, дающий уравнение того же вида, но на сей раз относящееся к диффузии. В гл. 43 (вып. 4) мы рассмотрели диффузию ионов в однородном газе и диффузию одного газа сквозь другой
Безвихревое течение жидкости; обтекание шара
Рассмотрим теперь пример, по существу, не такой уж хороший, потому что уравнения, которые мы будем использовать, на самом деле не описывают новый объект полностью, а отвечают лишь некоторым идеал
Освещение; равномерное освещение плоскости
В этом параграфе мы обратимся к совсем другой физической проблеме — мы ведь хотим показать большое разнообразие возможностей. На этот раз мы проделаем кое-что, что приведет нас к интегралу
Фундаментальное единство» природы
В этой главе мы хотели показать, что, изучая электростатику, вы одновременно учитесь ориентироваться во многих вопросах физики и что, помня об этом, можно выучить почти всю физику за несколько ле
Магнитное поле
Сила, действующая на электрический заряд, зависит не только от того, где он находится, но и от того, с какой скоростью он движется. Каждая точка в пространстве характеризуется двумя векторными вели
Электрический ток; сохранение заряда
Подумаем теперь о том, почему магнитные силы действуют на провода, по которым течет электрический ток. Для этого определим, что понимается под плотностью тока. Электрический ток состоит из движущ
Магнитная сила, действующая на ток
Теперь мы достаточно подготовлены, чтобы определить силу, действующую на находящуюся в магнитном поле проволоку, по которой идет ток. Ток состоит из заряженных частиц, движущихся по проволоке со с
Магнитное поле постоянного тока; закон Ампера
Мы видели, что на проволоку в магнитном поле, создаваемом, скажем, магнитом, действует сила. Из закона о том, что действие равно противодействию, можно ожидать, что, когда по проволоке протекает т
Магнитное поле прямого провода и соленоида; атомные токи
Можно показать, как пользоваться законом Ампера, определ
Относительность магнитныхи электрических полей
Когда мы сказали, что магнитная сила на заряд пропорциональна его скорости, вы, наверное, подумали: «Какой скорости? По отношению к какой системе отсчета?» Из определения В, данного в начале этой г
Преобразование токов и зарядов
Вы, вероятно, были обеспокоены сделанным нами упрощением, когда мы взяли одну и ту же скорость v для частицы и электронов проводимости в проволоке. Можно было бы вернуться назад и снова проделать
Суперпозиция; правило правой руки
Мы закончим эту главу еще двумя замечаниями по вопросам
Векторный потенциал
В этой главе мы продолжим разговор о магнитостатике, т, е. о постоянных магнитных полях и постоянных токах. Магнитное поле и электрические токи связаны нашими основными уравнениями:
Векторный потенциал заданных токов
Раз В определяется токами, значит, и А тоже. Мы хотим теп
Это векторное уравнение, конечно, распадается на три уравнения
Прямой провод
В качестве первого примера снова вычислим поле прямого провода, которое мы находили в предыдущем параграфе, пользуясь уравнением (14.2) и соображениями симметрии. Возьмем длинный прямой провод рад
Длинный соленоид
Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным пI на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каж
Поле маленькой петли; магнитный диполь
Воспользуемся методом векторного потенциала, чтобы найти магнитное поле маленькой петли с током. Как обычно, под словом «маленькая» мы просто подразумеваем, что нас интересуют поля только на больш
Векторный потенциал цепи
Нас часто интересует магнитное поле, создаваемое цепью проводов, в которой диаметр провода очень мал по сравнению с размерами всей системы. В таких случаях мы можем упростить уравнения для магнитн
Закон Био— Савара
В ходе изучения электростатики мы нашли, что электрическ
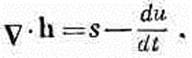

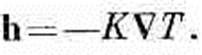
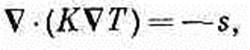


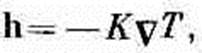
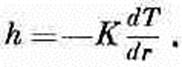
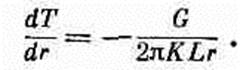

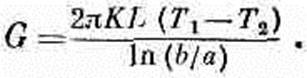
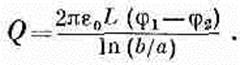
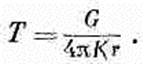


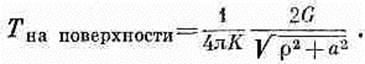







Новости и инфо для студентов