Численные методы решения краевых задач математической физики

Московский Государственный Институт Электронной Техники

(Технический Университет)

 

 

КУРСОВАЯ РАБОТА

по курсу «Численные методы»

на тему «Численные методы решения краевых задач

математической физики».

Вариант – 86

 

 

Выполнил: студент гр. МП-31

Михайлов С.С.

Проверил: преподаватель

Земсков В.Н.

 

Москва

2010

Постановка задачи

Задача:получить приблизительное решение данной краевой задачи уравнения в частных производных математической физики методом сеток.

(1)

 

 

Данное уравнение является уравнением гиперболического типа и физически отражает процесс колебания струны. Искомое решение U(x,y) - вертикальное отклонение струны в точке x в момент времени t.

Данная краевая задача состоит в нахождении функции U(x,y), удовлетворяющей уравнению, а также заданным начальным и граничным условиям.

Граничное условие 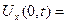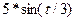определяет закон движения левого конца струны. Для правого конца в качестве граничного условия задано условие .

Начальные условия 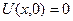и задают начальную форму струны и распределение скоростей в начальный момент времени.

 

 

Решение задачи с помощью явной разностной схемы

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам:

Аппроксимация дифференциального уравнения

Получаем конечно-разностную систему:

Аппроксимация 1-го начального условия

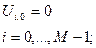(3)

Аппроксимация 1-го граничного условия

Аппроксимация краевого условия используется только для нахождения решения на границе i=0 в явном виде:

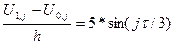
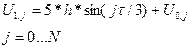(4)

Аппроксимация 2-го начального условия

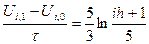
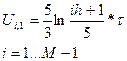(5)

Формула (5) используется на начальном этапе для вычисления значения функции U(x,y) на первом слое, по известным значениям функции на нулевом слое и на границе.

Аппроксимация 2-го граничного условия

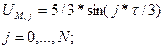
Устойчивость решения

(7) т.е. если это условие устойчивости не будет выполнено, то в процессе… Отсюда, в частности, получаем для явной схемы () условие устойчивости Куранта-Леви: .

Решение задачи с помощью неявной разностной схемы

Рассмотрим снова нашу краевую задачу. Для аппроксимации уравнения используем Т-образный пятиточечный шаблон.

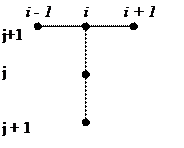
Уравнение аппроксимируется следующими уравнениями :

Аппроксимация дифференциального уравнения

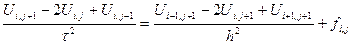(8)

Обозначим g=t/h и приведем (10) к виду удобному для применения метода прогонки:

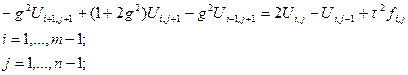(9)

Аппроксимация 1-го начального условия

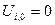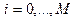, (10)

Аппроксимация 2-го начального условия

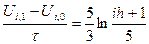
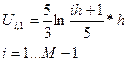(11)

Аппроксимация 2-го граничного условия

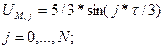(12)

Аппроксимация 1-го граничного условия

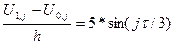
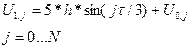(13)

Вычисления прогоночных коэффициентов

Обозначим , тогда, получим систему: получим прогоночные коэффициенты:

Практическая область применимости явной и неявной схем.

Используя неявную схему, можно находить негладкие решения разностным методом. Многие задачи математической физике, описывающие ударные процессы в…  

Приложение

Явная схема

function y=k_1(M,N)

h=1/M;

t=1/N;

if t>h

 

for i=1:10,disp(' ');end;

disp(' ВОЗМОЖНА НЕУСТОЙЧИВОСТЬ!!!');

disp('(невыполнено условие устойчивости Куранта-Леви:t<=h)!!!');

pause

end;

 

t2=t^2;

h2=h^2;

g=t2/h2;

 

U=zeros(M+1,N+1);

S=zeros(M+1);

 

for j=1:N+1

U(M+1,j)=0;

end;

 

U(1:M,1)=-sin(2*(1:M)'*h*pi);

 

U(1:M,2)=U(1:M,1)-t*sin(2*(1:M)'*h*pi);

 

f=@(x,t)sin(2*h*pi).*(2*pi*pi*t2-4*pi*t*sqrt(2)+5)./(0.5*pi*pi*pi*t*t*t-(3*pi*pi*t2/sqrt(2))+3*pi*t-1/sqrt(2));

 

for k=2:N

U(2:M,k+1)=g^2*U(3:M+1,k)+2*(1-g^2)*U(2:M,k)+...

g^2*U(1:M-1,k)-U(2:M,k-1)+t^2*f((2:M)'*h*pi,k*t*pi/2^.5);

end;

U(1,3:N+1)=U(2,3:N+1)-2*h./((3:N+1)*t-1);

 

mesh(U);end

 

 

Построение двумерных параметрических графиков

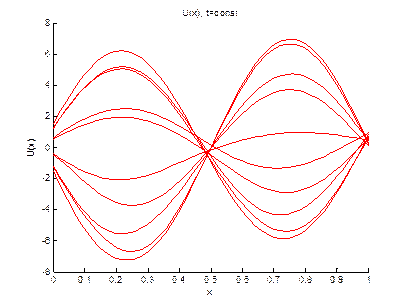
u[10x10]

-0.2694 -0.6292 -0.7352 -0.6487 -0.4149 -0.1136 0.1764	0.4006 0.5376 0.5940 0
-0.5657 -1.0067 -1.1763 -1.0379 -0.6638 -0.1817 0.2822	0.6410 0.8601 0.9505 0
-0.8179 -1.2694 -1.3558 -1.1293 -0.6869 -0.1517 0.3599	0.7664 1.0330 1.1682 0
-0.8038 -1.1852 -1.1898 -0.9271 -0.5137 -0.0484 0.3946	0.7670 1.0466 1.2350 0
-0.4953 -0.7068 -0.6751 -0.4859 -0.2180 0.0787 0.3788	0.6688 0.9392 1.1824 0
-0.0018 0.0195 0.0470 0.0768 0.1205 0.1987 0.3305	0.5247 0.7763 1.0666 0
0.4883 0.7267 0.7334 0.5996 0.4309 0.3112 0.2936	0.4010 0.6287 0.9476 0
0.7793 1.1374 1.1415 0.9353 0.6597 0.4263 0.3121	0.3556 0.5549 0.8730 0
0.7267 1.0778 1.1461 1.0115 0.7699 0.5343 0.4006	0.4187 0.5875 0.8681 0
0.2255 0.5925 0.8181 0.8346 0.7232 0.5983 0.5409	0.5836 0.7208 0.9249 0
-1.0002 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000	0.8000 0.9000 1.0000 0

Неявная схема

function y=k_2(M,N)

h=1/M; t=1/N;

u=zeros(M+1,N+1);

h2=h^2; t2=t^2; g2=t2/h2;

for j=1:N+1

u(M+1,j)=0;

end;

A=zeros(M,1);C=zeros(M+1,1);B=A;A1=A;F=C;B1=C;

for i=1:M

A(i)=g2/2;

B(i+1)=g2/2;

C(i+1)=1+g2;

F(i+1)=-10*sin(2*i*h*pi);

end;

A(M)=0; B(1)=0;

C(1)=1+h*g2+g2;

C(M+1)=1;

F(1)=0; F(M+1)=0;

A1(1)=B(1)/C(1);

B1(1)=F(1)/C(1);

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,2)=B1(M+1);

for i=M:-1:1

u(i,2)=A1(i)*u(i+1,2)+B1(i);

end;

for i=1:M-1

A(i)=g2; B(i+1)=g2;

C(i+1)=1+2*g2;

end

A(M)=0; B(1)=2*g2;

C(1)=1+2*h*g2+2*g2;

C(M+1)=1;

A1(1)=B(1)/C(1);

B1(1)=F(1)/C(1);

F(1)=0;

for j=2:N

for i=1:M-1

F(i+1)=2*u(i+1,j)-u(i+1,j-1)+5*t2*sin(2*i*pi*h)*(2*pi*pi*t2-4*pi*t*sqrt(2)+5)/(0.5*pi*pi*pi*t*t*t-(3*pi*pi*t2/sqrt(2))+3*pi*t-1/sqrt(2));

end;

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

F(M+1)=0;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,j+1)=B1(M+1);

for i=M:-1:1

u(i,j+1)=A1(i)*u(i+1,j+1)+B1(i);

end;

end;

contour(u,20);pause;

for j=0:N,

i=1:1:M;

u1=u(i,j+1);

plot(i,u1);

end;

mesh(u); end

 

Построение двумерных параметрических графиков

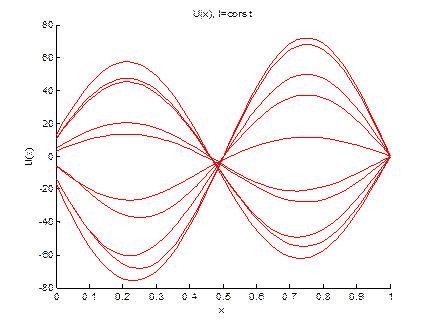
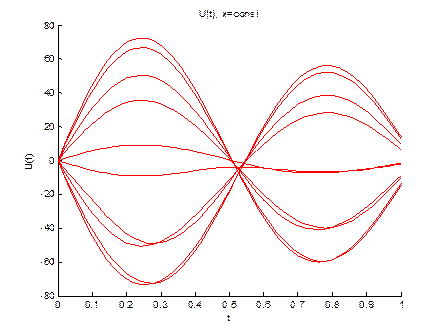
u[10x10]

0.0514 -0.3180 -0.3556 -0.2176 0.0462 0.3547 0.6299	0.8213 0.9133 0.9210 0
-0.4797 -0.8027 -0.8629 -0.6421 -0.2199 0.2736 0.7140	1.0201 1.1674 1.1798 0
-0.7949 -1.1599 -1.1368 -0.8150 -0.3141 0.2345 0.7155	1.0554 1.2333 1.2741 0
-0.7976 -1.1350 -1.0700 -0.7368 -0.2767 0.1955 0.6019	0.9020 1.0895 1.1840 0
-0.4933 -0.6975 -0.6483 -0.4379 -0.1599 0.1210 0.3749	0.5949 0.7855 0.9533 0
0.0001 -0.0003 -0.0027 -0.0070 -0.0052 0.0202 0.0913	0.2247 0.4227 0.6704 0
0.4935 0.6965 0.6407 0.4221 0.1557 -0.0570 -0.1466	-0.0833 0.1245 0.4373 0
0.7986 1.1321 1.0548 0.7176 0.2982 -0.0511 -0.2322	-0.2089 0.0001 0.3387 0
0.7985 1.1503 1.1055 0.8009 0.4061 0.0724 -0.1019	-0.0826 0.1091 0.4172 0
0.4935 0.7693 0.8071 0.6721 0.4713 0.3045 0.2355	0.2848 0.4380 0.6596 0
0.0000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000	0.8000 0.9000 1.0000 0