рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Физика
- /
- Равновесные состояния пучка.
Реферат Курсовая Конспект
Равновесные состояния пучка.
Равновесные состояния пучка. - раздел Физика, Транспортировка сильноточных импульсных РЭП в вакууме Для Осуществления Транспортировки Электронного Пучка С Высокой Эффективностью...
Для осуществления транспортировки электронного пучка с высокой эффективностью на значительные расстояния необходимо, чтобы пучок находился в некотором равновесном состоянии, при котором имеет место компенсация всех сил, действующих на частицы пучка. Установление конкретного типа равновесного состояния зависит от множества факторов, в том числе от переходного процесса, который происходит вблизи плоскости инжекции пучка в дрейфовое пространство. В теории подробно исследованы два типа продольно однородных равновесий: конфигурации пучков с резкими границами, когда отсутствует термодинамическое равновесие; и конфигурации с размытыми границами, в которых имеет место распределение Максвелла электронов по скоростям в системе покоя пучка как целого. Рассмотрим несколько наиболее простых равновесных конфигураций для случая однородного по длине цилиндрического пучка с резкими границами [4]. В этом анализе мы пренебрежем тепловым разбросом электронов по скоростям, а влияние плазмы учтем введением степени нейтрализации пучка по заряду 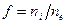 , которую будем считать величиной постоянной. Для равновесия сил, действующих на электроны пучка в радиальном направлении, необходимо выполнить следующее условие:
, которую будем считать величиной постоянной. Для равновесия сил, действующих на электроны пучка в радиальном направлении, необходимо выполнить следующее условие:
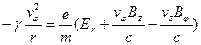 , (6.5)
, (6.5)
в котором использованы самосогласованные электрическое и магнитное поля, удовлетворяющие уравнениям Максвелла:
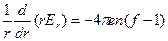 (6.6)
(6.6)
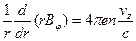 (6.7)
(6.7)
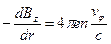 . (6.8)
. (6.8)
Эта система четырех уравнений (6.5-6.8) является незамкнутой относительно шести неизвестных величин 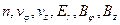 , и для решения ее необходимо дополнить некоторыми предположениями.
, и для решения ее необходимо дополнить некоторыми предположениями.
Предположим, что нам известна зависимость компоненты магнитного поля 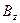 от радиуса
от радиуса  :
: 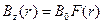 , а плотность электронов пучка
, а плотность электронов пучка  не зависит от радиуса. Также для простоты будем считать, что объемный заряд электронов полностью скомпенсирован холодными неподвижными ионами. Выражая компоненты скоростей из соотношений (6.7-6.8) и подставляя их в (6.5), получим:
не зависит от радиуса. Также для простоты будем считать, что объемный заряд электронов полностью скомпенсирован холодными неподвижными ионами. Выражая компоненты скоростей из соотношений (6.7-6.8) и подставляя их в (6.5), получим:
 . (6.9)
. (6.9)
Это дифференциальное уравнение решить аналитически очень трудно, поскольку в правой его части стоит 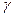 - фактор, который сложным образом выражается через скорости, а они, в свою очередь, через производные компонентов магнитного поля. Но, если пренебречь правой частью равенства (6.9) по сравнению с его первым слагаемым в левой части, что оказывается оправданным в случае, когда выполнено условие:
- фактор, который сложным образом выражается через скорости, а они, в свою очередь, через производные компонентов магнитного поля. Но, если пренебречь правой частью равенства (6.9) по сравнению с его первым слагаемым в левой части, что оказывается оправданным в случае, когда выполнено условие:
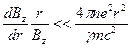 , (6.10)
, (6.10)
что эквивалентно превышению тока пучка над током Альфвена 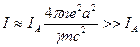 (тем самым мы пренебрегли центробежной силой), тогда все неизвестные величины выражаются через
(тем самым мы пренебрегли центробежной силой), тогда все неизвестные величины выражаются через 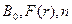 по следующим формулам:
по следующим формулам:
 , (6.11)
, (6.11)
где введена новая функция:
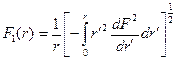 (6.12)
(6.12)
Рассмотрим частный случай подобного равновесного состояния пучка, когда он вращается как целое с угловой скоростью 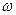 . Из выражения для азимутальной скорости
. Из выражения для азимутальной скорости 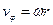 и соотношения (6.8) следует:
и соотношения (6.8) следует:
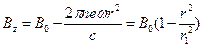 , (6.13)
, (6.13)
где 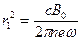 . Подставляя выражение для функции
. Подставляя выражение для функции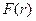 из (6.13) в формулу (6.12), легко получить выражение для функции
из (6.13) в формулу (6.12), легко получить выражение для функции 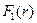 и полного тока пучка
и полного тока пучка 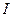 :
:
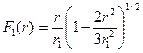 (6.14)
(6.14)
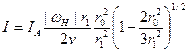 (6.15)
(6.15)
где 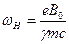 - циклотронная частота электронов в магнитном поле на оси пучка, а
- циклотронная частота электронов в магнитном поле на оси пучка, а 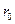 - радиус пучка. Величина полного тока
- радиус пучка. Величина полного тока 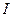 достигает своего максимума при выполнении
достигает своего максимума при выполнении 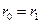 , но тогда нарушится условие (6.10), позволяющее пренебречь центробежной силой в выражении (6.9). Учитывая это условие, можно получить, что
, но тогда нарушится условие (6.10), позволяющее пренебречь центробежной силой в выражении (6.9). Учитывая это условие, можно получить, что 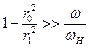 , которое удовлетворяется только в случае
, которое удовлетворяется только в случае 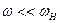 , и тогда в (6.15) можно подставлять
, и тогда в (6.15) можно подставлять  . Рассмотренное равновесное состояние называют «бессиловым», так как в пренебрежении центробежной силой сумма остальных сил в нашем случае равна нулю.
. Рассмотренное равновесное состояние называют «бессиловым», так как в пренебрежении центробежной силой сумма остальных сил в нашем случае равна нулю.
Рассмотрим еще одну модель аксиально-симметричного пучка с неоднородным распределением плотности электронов по радиусу 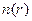 , вращающегося с постоянной угловой скоростью
, вращающегося с постоянной угловой скоростью 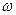 , и с постоянной продольной скоростью
, и с постоянной продольной скоростью  . Из уравнений (6.6-6.8) в указанных предположениях легко получить следующие выражения для полей:
. Из уравнений (6.6-6.8) в указанных предположениях легко получить следующие выражения для полей:
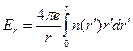
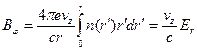 (6.16)
(6.16)
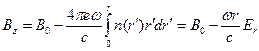
Подставляем эти выражения в уравнение (6.5), из которого получаем 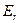 :
:
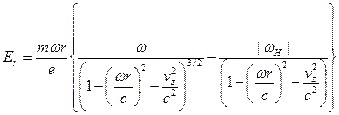 (6.17)
(6.17)
Из этого соотношения можно получить равновесное распределение плотности в пучке:
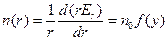 , (6.18)
, (6.18)
где 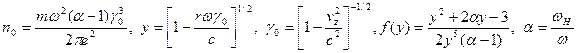 . Это решение существует только в случае
. Это решение существует только в случае 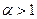 . Граница пучка определяется из условия
. Граница пучка определяется из условия  , что дает радиус пучка
, что дает радиус пучка 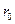 :
:
 . (6.18)
. (6.18)
Зная плотность, продольную скорость и радиус пучка, легко получить его полный ток:
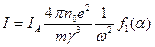 , (6.19)
, (6.19)
где функция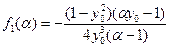 , а
, а 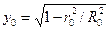 . Асимптотики функции
. Асимптотики функции 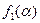 имеют следующий вид:
имеют следующий вид: 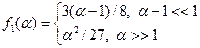 .
.
Из анализа зависимости полного тока пучка от параметра очевидно, что с его ростом ток пучка увеличивается, и для реализации режима
очевидно, что с его ростом ток пучка увеличивается, и для реализации режима  необходимо выполнение условия
необходимо выполнение условия  . Следует отметить, что с ростом
. Следует отметить, что с ростом 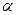 также растет и неоднородность распределения плотности тока пучка по радиусу, она превалирует при больших радиусах, таким образом пучок становится трубчатым.
также растет и неоднородность распределения плотности тока пучка по радиусу, она превалирует при больших радиусах, таким образом пучок становится трубчатым.
Равновесные состояния ленточного пучка
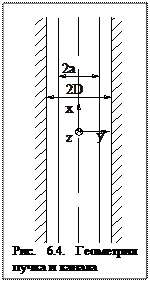 Для простоты рассмотрения будем предполагать, что стационарный пучок бесконечный и однородный в направлении осей X и Z (см. рис.6.4), распространяется в направлении Z внутри плоского щелевого канала, образованного двумя идеально проводящими стенками. Кроме того, внешними условиями, например, геометрией диода задано распределение плотности тока пучка по сечению, а также задана одинаковая начальная энергия электронов. Пренебрежем также и тепловым разбросом электронов по скоростям. Из уравнений Максвелла следует, что электрическое поле потенциально и имеет одну ненулевую компоненту
Для простоты рассмотрения будем предполагать, что стационарный пучок бесконечный и однородный в направлении осей X и Z (см. рис.6.4), распространяется в направлении Z внутри плоского щелевого канала, образованного двумя идеально проводящими стенками. Кроме того, внешними условиями, например, геометрией диода задано распределение плотности тока пучка по сечению, а также задана одинаковая начальная энергия электронов. Пренебрежем также и тепловым разбросом электронов по скоростям. Из уравнений Максвелла следует, что электрическое поле потенциально и имеет одну ненулевую компоненту 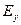 , а магнитное поле, напротив, имеет
, а магнитное поле, напротив, имеет 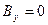 . Тогда интегрируя уравнения Максвелла, получим:
. Тогда интегрируя уравнения Максвелла, получим:
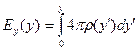 ,
,
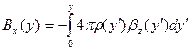 , (6.19)
, (6.19)
 ,
,
где 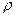 -плотность электронов в пучке,
-плотность электронов в пучке, 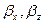 - компоненты скорости электронов, деленные на скорость света. Из предположения, что пучок холодный и находится в равновесии, т.е. не двигается вдоль направления
- компоненты скорости электронов, деленные на скорость света. Из предположения, что пучок холодный и находится в равновесии, т.е. не двигается вдоль направления 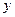 , следует, что
, следует, что 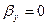 , кроме того, должно выполняться условие равенства нулю силы в поперечном направлении:
, кроме того, должно выполняться условие равенства нулю силы в поперечном направлении:
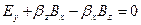 . (6.20)
. (6.20)
Помножим уравнение (6.20) на 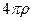 и подставим вместо
и подставим вместо 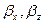 их выражения из (6.19), тогда получим:
их выражения из (6.19), тогда получим:
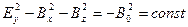 , (6.21)
, (6.21)
где 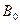 - есть магнитное поле в центральной плоскости пучка. Это соотношение очень похоже на известный из электродинамики инвариант преобразования полей из одной системы координат в другую, но в прямую он здесь неприменим, так как все электроны двигаются с различными продольными скоростями. Зная распределение плотности тока в пучке, легко найти компоненту
- есть магнитное поле в центральной плоскости пучка. Это соотношение очень похоже на известный из электродинамики инвариант преобразования полей из одной системы координат в другую, но в прямую он здесь неприменим, так как все электроны двигаются с различными продольными скоростями. Зная распределение плотности тока в пучке, легко найти компоненту 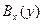 :
:
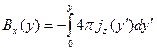 (6.22)
(6.22)
Воспользовавшись соотношениями (6.21) и (6.22), легко получить выражение для  , в которое входит неизвестная компонента поля
, в которое входит неизвестная компонента поля 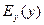 . Из выражения для закона сохранения энергии электрона:
. Из выражения для закона сохранения энергии электрона:  , можно получить связь производной от гамма-фактора электрона с величиной электрического поля:
, можно получить связь производной от гамма-фактора электрона с величиной электрического поля:
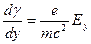 . (6.23)
. (6.23)
Далее, используя известное выражение для гамма-фактора через компоненты скорости 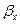 ,
,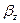 , а также условие равновесия (6.20), составим квадратное уравнение, из решения которого находится выражение для величины
, а также условие равновесия (6.20), составим квадратное уравнение, из решения которого находится выражение для величины 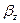 :
:
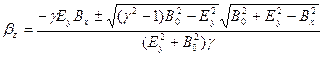 (6.24)
(6.24)
В итоге имеем систему двух дифференциальных уравнений на две неизвестные 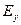 и
и 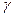 :
:
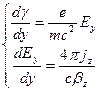 , (6.25)
, (6.25)
в которой компонента скорости 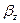 тоже выражена через них и другие известные величины (см. (6.24)). Заметим, что в выражении (6.24) среди корней квадратного уравнения надо выбрать положительный наибольший по модулю корень. Другому значению соответствует неустойчивое решение. Численно решая систему уравнений (6.25) для различных величин
тоже выражена через них и другие известные величины (см. (6.24)). Заметим, что в выражении (6.24) среди корней квадратного уравнения надо выбрать положительный наибольший по модулю корень. Другому значению соответствует неустойчивое решение. Численно решая систему уравнений (6.25) для различных величин 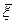 , характеризующих степень заполнения пучком канала и определяемых соотношением:
, характеризующих степень заполнения пучком канала и определяемых соотношением:
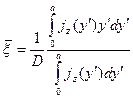 ,
,
в работе [5] были получены зависимости погонного тока пучка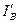 , нормированного на значение погонного предельного вакуумного тока в бесконечном магнитном поле
, нормированного на значение погонного предельного вакуумного тока в бесконечном магнитном поле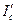 :
:
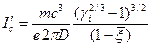 ,
,
как функции от магнитного поля на оси 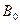 , нормированного на некоторое критическое магнитное поле, равное:
, нормированного на некоторое критическое магнитное поле, равное:
 .
.
 При численном решении в качестве граничных условий были взяты следующие соотношения
При численном решении в качестве граничных условий были взяты следующие соотношения 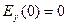 и
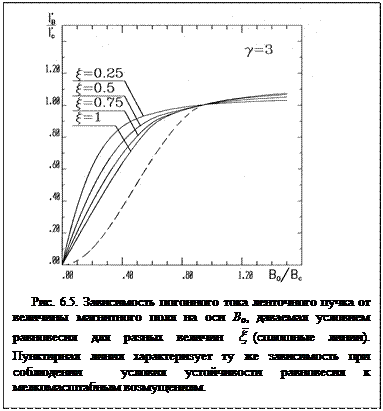
и 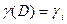 . Результаты расчетов, приведенные на рис. 6.5 для случая
. Результаты расчетов, приведенные на рис. 6.5 для случая  , отражают общий характер зависимости тока пучка от магнитного поля и для других величин
, отражают общий характер зависимости тока пучка от магнитного поля и для других величин 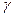 , что позволяют утверждать, что эта зависимость носит универсальный характер. Таким образом, для достижения равновесного состояния ленточного пучка с током, близким или равным предельному вакуумному, необходимо создать индукцию магнитного поля в щелевом канале, превышающую
, что позволяют утверждать, что эта зависимость носит универсальный характер. Таким образом, для достижения равновесного состояния ленточного пучка с током, близким или равным предельному вакуумному, необходимо создать индукцию магнитного поля в щелевом канале, превышающую 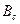 .
.
– Конец работы –
Эта тема принадлежит разделу:
Транспортировка сильноточных импульсных РЭП в вакууме
На сайте allrefs.net читайте: "Транспортировка сильноточных импульсных РЭП в вакууме"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Равновесные состояния пучка.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов