Крупномасштабные неустойчивости.

Рассмотрим устойчивость равновесия по отношению к длинноволновым возмущениям.

Диокотронная неустойчивость.

Известно, что для сильноточных РЭП наиболее опасной является диокотронная неустойчивость. Она возникает в результате поперечного дрейфа электронов в скрещенных полях: собственном электрическом и внешнем магнитном поле. Линейная и нелинейная стадии развития такой неустойчивости рассматривались в работах [8,9]. Рассмотрим подробнее наиболее простую модель - линейную стадию развития диокотронной неустойчивости. Будем исходить из следующих предположений: невозмущенные продольная скорость и плотность электронов не зависят от поперечных координат, а поперечная составляющая, обусловленная дрейфом, мала по сравнению со скоростью света. Также будем считать для простоты, что магнитное поле в канале существенно превышает предел, определяемый критерием (6.31). Тогда основные уравнения, описывающие развитие неустойчивости, имеют следующий вид:

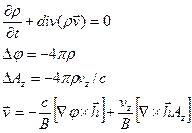(6.33)

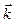Ищем решение этой системы в виде бегущей волны с волновым вектором , направленным перпендикулярно магнитному полю, т.е. вдоль оси 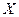. Линеаризуя систему уравнений (6.33), можно получить инкремент развития неустойчивости в следующем виде:

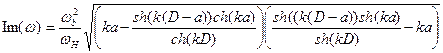, (6.34)

где 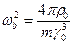- квадрат плазменной частоты пучка, а 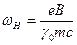- циклотронная частота электронов во внешнем магнитном поле 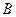. Поведение инкремента диокотронной неустойчивости, нормированного на величину 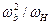, от величины 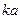при разных степенях заполнения пучком сечения канала 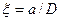демонстрирует рис.6.6. Из него видно, что максимум инкремента, равный достигается в случае очень тонкого пучка (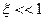) вблизи значения 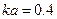. В области 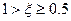неустойчивость не возбуждается. Из аппроксимации кривых, представленных на рис.6.6 для разных 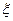, было получено следующее приближенное выражение для максимума инкремента:

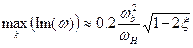. (6.35)

Это выражение может быть использовано в качестве оценки и в случае приближения к границе устойчивости пучка по отношению к коротковолновым возмущениям, когда (см. соотношение (6.31)). Очевидно, что результатом развития диокотронной неустойчивости на линейной стадии является модуляция пучка по плотности заряда, которая на нелинейной стадии, как показано в теории и наблюдалось в экспериментах, приводит к образованию токовых нитей внутри сечения пучка.

Неустойчивости частично или полностью нейтрализованных пучков

Как известно, для решения проблемы устойчивости сильноточных пучков вначале необходимо найти равновесное состояние пучка, а затем решать начальную задачу о развитии во времени малых по амплитуде колебаний. Но в условиях равновесия параметры сильноточных пучков, как правило, неоднородны в пространстве, вследствие чего уравнения на малые колебания содержат переменные коэффициенты. Для упрощения процесса нахождения решения, обычно рассматривают пучки, частично или полностью скомпенсированные по заряду, поскольку равновесные состояния для них наиболее просты из-за отсутствия провисания потенциала. Среди наиболее известных и сравнительно простых в рассмотрении неустойчивостей нейтрализованного пучка является неустойчивость Пирса[9], обусловленная конечными продольными размерами области транспортировки пучка. Рассмотрение проведем методом, описанным в книге [4]. Будем исходить из следующих предположений. Пространство дрейфа представляет собой область, заключенную внутри полой аксиально-симметричной цилиндрической оболочки длиной 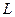и радиусом , закрытой с торцов тонкими фольгами, через одну из которых пучок влетает внутрь оболочки, а через другую вылетает наружу. Стенки оболочки и фольги находятся под нулевым потенциалом. Внутри оболочки создано внешнее однородное магнитное поле, удовлетворяющее условию: 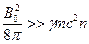, т.е. такой величины, что по отношению к нему можно пренебречь вкладом собственного магнитного поля пучка. Пусть пучок заполняет все пространство дрейфа, а заряд его полностью скомпенсирован зарядом неподвижных ионов, вследствие чего параметры пучка можно выбрать однородными по его сечению. Электроны в пучке на входе в пространство дрейфа будем считать моноэнергетическими, а функцию распределения их произведением двух дельта-функций по продольной и поперечной компонентам импульса:

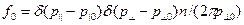. (6.36)

Исходя из малости собственного магнитного поля пучка в сравнении с внешним полем, а также условия сохранения адиабатического инварианта 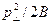, можно заключить, что поперечный импульс электронов практически не изменяется, тогда поперечную скорость электрона можно выразить следующим образом: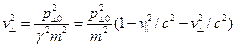и далее: . Подставляя это соотношение в выражение для продольного импульса, легко получить, что . Далее дифференцируя его по времени, получим следующий результат: , где величинойобозначено выражение 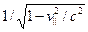. Из выполнения неравенства: 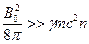следует, что движение электронов пучка происходит только в продольном направлении, следовательно, можно рассматривать только потенциальные возмущения электрического поля. Обозначив возмущение продольной скорости электрона - 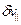и пренебрегая возмущением поперечной скорости, напишем систему уравнений, включающую в себя уравнение движения электрона в продольном направлении, уравнение Пуассона на потенциал, который тоже является возмущением, а также уравнение неразрывности:

(6.36)

Решая систему уравнений (6.36) в цилиндрической системе координат 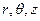с следующими граничными условиями:

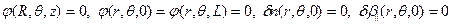, (6.37)

ищем решение для всех переменных в виде бегущей волны . Исключив переменные и 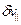из дальнейшего рассмотрения, получим следующее уравнение на потенциал:

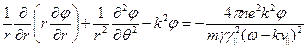, (6.38)

которое решаем методом разделения переменных, т.е. ищем решение в виде: 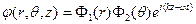. Тогда из условий периодичности по углу 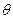в качестве подойдут только функции 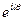для любых целых значений 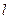, а в качестве соответствующих им радиальных функций необходимо выбрать функции Бесселя , для которых коэффициент 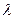должен быть выбран из условия равенства нулю потенциала на поверхности цилиндрической оболочки, т.е. 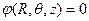. В этом случае в качестве параметра 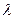можно выбрать любые корни 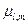номера 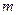функции Бесселя 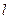порядка. В итоге, общий вид решения для потенциала в случае произвольных значений и 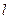будет иметь следующий вид:

. (6.39)

Подставив его в соотношение (6.38), получим характеристическое уравнение, определяющее значения :

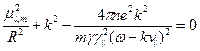, (6.40)

которое имеет четыре различных корня . Очевидно, общее решение уравнения (6.38) будет иметь вид суммы из четырех слагаемых по числу решений (6.40):

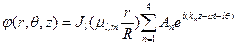. (6.41)

Таким образом, для определения четырех неизвестных констант 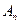имеется четыре граничных условия, последних из набора (6.37). К сожалению, решить уравнение (6.40) при произвольном соотношении величин 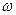и 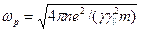невозможно, поэтому рассмотрим только случай 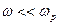. Обозначив 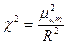, перепишем уравнение (6.40) в более простом виде:

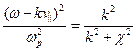. (6.42)

У этого уравнения есть два решения в коротковолновой области, т.е. в случае :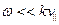

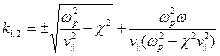, (6.43)

и еще два решения в длинноволновой области, 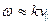(см. рис. 6.7):

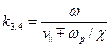(6.45)

Используя значения для четырех корней характеристического уравнения, а также четыре граничные условия, найдем условие, при котором хотя бы одна константа 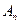не равна нулю, которое и дает дисперсионное уравнение:

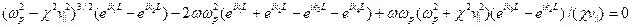Из этого уравнения можно найти интервалы, в которых решения этого уравнения имеют положительную мнимую часть 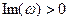, что соответствует возбуждению неустойчивости:

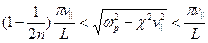, где 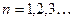(6.46)

Очевидно, что неравенству (6.46) будут удовлетворять только такие значения 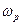, которые описываются выражением: 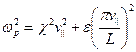, где 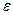находится в интервале 0.5¸1. Тогда в случае длинного пространства дрейфа второй частью этого выражения можно пренебречь, и найти из него минимальное значение 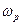, при котором в пучке будет развиваться пирсовская неустойчивость:

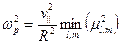. (6.47)

Минимум в (6.47) достигается при 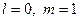, для которых 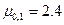. Таким образом, наименьший порог по плотности при возбуждении пирсовской неустойчивости имеет аксиально-симметричная мода, описываемая функцией Бесселя нулевого порядка, которая обращается в ноль первый раз при 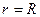. Выразив из (6.47) плотность электронов и умножив ее на заряд, продольную скорость и площадь сечения пучка, найдем критический ток пучка:

. (6.47)

При превышении током пучка величины 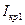в системе будет происходить раскачка колебаний с инкрементом 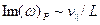, в результате чего образуется виртуальный катод, и часть электронного тока отразится в обратном направлении.

Если сравнить значение предельного тока пучка, ограниченного своим объемным зарядом при его частичной компенсации ионным фоном со степенью нейтрализации :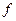

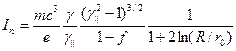, (6.48)

с величиной пирсовского тока, то их отношение при одинаковом заполнении пространства дрейфа будет иметь следующий вид:

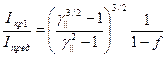. (6.49)

Очевидно, что при отношении токов (6.49) меньше единицы, ток пучка будет определяться равновесием, в противоположном случае – устойчивостью по отношению к возбуждению низкочастотных колебаний.

 

Неустойчивость Будкера –Бунемана

При рассмотрении пирсовской неустойчивости мы считали ионы, нейтрализующие заряд пучка, покоящимися. Как показано в работе [10], можно учесть и их движение. Будем предполагать, что электронный пучок, полностью нейтрализованный по заряду, движется в бесконечно длинной трубе в условиях сильного продольного магнитного поля, удовлетворяющего такому же условию, что и при рассмотрении пирсовской неустойчивости, но ограниченного сверху:

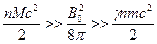. (6.50)

В этих условиях ионная плазменная частота 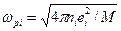будет превышать ионную циклотронную, поэтому ионы можно считать незамагниченными. В сделанных предположениях система уравнений для малых электростатических колебаний нейтрализованного пучка будет иметь следующий вид:

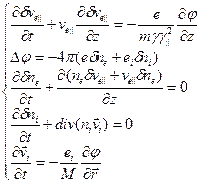, (6.51)

в которой для возмущенных значений использованы обозначения 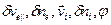, а для невозмущенных, т.е. равновесных -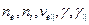. На эту систему уравнений, учитывая большую протяженность дрейфового пространства в продольную направлении, накладывается всего одно граничное условие на потенциал:

(6.52)

Предполагая, что все возмущенные параметры зависят от продольной координаты 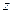и времени 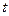также как и у бегущей волны, т.е. , решаем систему уравнений (6.51) и сводим ее к одному уравнению на потенциал:

. (6.53)

Аналогично рассмотрению пирсовской неустойчивости, для потенциала ищем решение в общем виде, удовлетворяющем граничному условию (6.52):

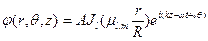. (6.54)

В итоге, мы находим условие существования ненулевого решения, которое представляет собой дисперсионное уравнение:

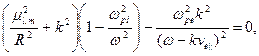(6.55)

в котором использовано обозначение .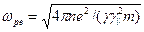

Из анализа этого уравнения [4] следует, что решения с 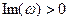существует только в области частот 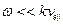, причем из условий:

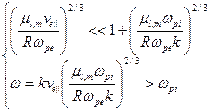(6.56)

можно найти критический ток пучка, выше которого происходит возбуждение неустойчивости Будкера-Бунемана:

. (6.57)

Исходя из условия для частоты 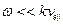, при котором существует эта неустойчивость, можно сделать вывод, что критические токи для неустойчивостей Пирса и Будкера –Бунемана практически совпадают. Различаются эти неустойчивости механизмом возбуждения, у первой он происходит посредством положительной обратной связи через внешнюю электрическую цепь, и поэтому произведение времени пролета электроном пространства дрейфа 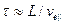на ее инкремент не зависит от длины системы. В отличие от пирсовской неустойчивость Будкера – Бунемана развивается за счет положительной обратной связи, создаваемой ионным движением. Следовательно, если произведение времени пролета на инкремент возбуждения неустойчивости Будкера – Бунемана :

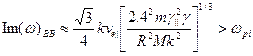, (6.57)

мало по сравнению с единицей, то возбуждается неустойчивость Пирса, для которой это произведение всегда близко к единице. И, наоборот, если , то возбуждается неустойчивость Будкера –Бунемана, как обладающая большим инкрементом.