рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- МОМЕНТ ИМПУЛЬСА
Реферат Курсовая Конспект
МОМЕНТ ИМПУЛЬСА
МОМЕНТ ИМПУЛЬСА - раздел Механика, ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА Мы Уже Рассмотрели Свойства Момента Импульса Одной Частицы, Который Был Связа...
Мы уже рассмотрели свойства момента импульса одной частицы, который был связан с ее движением в пространстве и определялся как
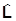 =
= 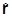 ´
´ 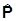
Это есть орбитальный момент. Теперь мы хотим обобщить это понятие, для чего получим его несколько иным способом - из симметрийных соображений.
Рассматриваем систему нескольких частиц с волновой функцией
y(r1,...rN) º y(ra).
Произведем вращение системы координат на угол dj (вектор dj)направлен по оси вращения, а его модуль равен углу поворота). Это означает, что физическая система осталась той же самой, а приборы повернулись на угол dj. Радиусы- векторы изменятся:
r¢a = ra + dra , dra=dj´ra.
Преобразуются и значения y - функции, но так как в «новую» точку ra «придет» «старая» точка ra -dra,то должно быть
y¢(ra) = y(ra-dra).
Разлагая в ряд Тейлора, найдем:
y¢(ra) = y(ra-dra) = y(ra) -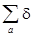 ra
ra 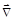 ay(ra) = (
ay(ra) = (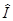 -
-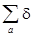 ra
ra 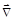 a) y(ra)
a) y(ra)
= (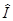 -
-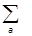 (dj´ra)
(dj´ra)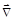 a) y(ra) = (
a) y(ra) = (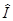 -dj
-dj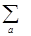 ra
ra 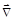 a) y(ra) º
a) y(ra) º
º (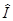 -
-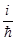 dj
dj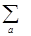 ra ´ (-i
ra ´ (-i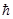
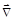 a)) y(ra) = (
a)) y(ra) = (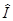 -
- 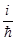 dj
dj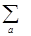
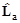 )y(ra).
)y(ra).
Итак,
y¢(ra) = (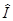 -
-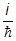 dj
dj 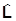 )y(ra), (*),
)y(ra), (*),
где
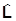 =
=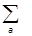
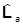 =
=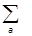
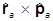 (**)
(**)
В данном случае мы ничего нового не получили. Но важно, что момент импульса можно трактовать двумя способами. Согласно определению (*), оператор 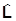 описывает преобразование волновой функции при малом вращении, т.е.
описывает преобразование волновой функции при малом вращении, т.е. 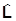 является генератором вращения. Согласно определению (**) оператор
является генератором вращения. Согласно определению (**) оператор 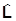 выражается через координаты и импульсы так же, как в классической механике. Еще раз: в данном случае получилось, что это одно и то же. Но в общей ситуации определение (*) может оказаться более общим. Оператор (**) действует только на координаты волновой функции. Но у нее могут быть и другие какие-то переменные, на которые (**) не действует, а (*) - действует.
выражается через координаты и импульсы так же, как в классической механике. Еще раз: в данном случае получилось, что это одно и то же. Но в общей ситуации определение (*) может оказаться более общим. Оператор (**) действует только на координаты волновой функции. Но у нее могут быть и другие какие-то переменные, на которые (**) не действует, а (*) - действует.
И такие дополнительные переменные действительно существуют у многих частиц (прежде всего у электрона). Это - спиновые переменные, являющиеся внутренними, врожденными степенями свободы частицы, никак не связанными с координатами. Обозначая их буквой s, запишем волновую функцию одной частицы как
y = y(r,s),
и в полной аналогии с рассмотренным частным случаем введем по определению оператор полного момента импульса как генератор вращений, т.е. преобразующий волновую функцию по закону
y¢(r,s) = (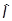 -
- 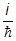 dj
dj )y(r,s).
)y(r,s).
Оператор  можно представить в виде двух слагаемых:
можно представить в виде двух слагаемых:
 =
=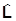 +
+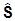 .
.
Оператор 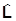 есть рассмотренный ранее оператор орбитального момента, который действует только на координаты. Оператор
есть рассмотренный ранее оператор орбитального момента, который действует только на координаты. Оператор 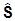 есть новый оператор - оператор спина, который действует только на спиновые переменные s. Оператор спина можно определить как оператор
есть новый оператор - оператор спина, который действует только на спиновые переменные s. Оператор спина можно определить как оператор  ,действующий в системе покоя частицы. Значит это действительно внутренний, врожденный момент импульса частицы.
,действующий в системе покоя частицы. Значит это действительно внутренний, врожденный момент импульса частицы.
Найдем правила коммутации  с операторами других физических величин. Пусть физическая величина F- векторная, и ей соответствует векторный оператор
с операторами других физических величин. Пусть физическая величина F- векторная, и ей соответствует векторный оператор  . Установим закон преобразования среднего значения Fпо произвольному состоянию y. С одной стороны имеем:
. Установим закон преобразования среднего значения Fпо произвольному состоянию y. С одной стороны имеем:
dF ºdá ñy = áy¢ê
ñy = áy¢ê êy¢ñ-áyê
êy¢ñ-áyê êyñ »
êyñ »
áyê(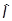 +
+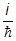 dj
dj )
) (
(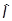 –
– 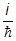 dj
dj )êyñ @
)êyñ @ 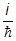 áyê[dj
áyê[dj ,
, ]êyñ.
]êyñ.
С другой стороны, как и для всякой векторной величины,
dF = dj´F = djáyê êyñ = áyêdj´
êyñ = áyêdj´ êyñ.
êyñ.
Сравнение дает
[ ,dj
,dj ] = i
] = i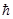 dj´
dj´ .
.
Проектируем на ось 1:
[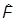 1,dj1
1,dj1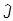 1+dj2
1+dj2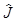 2 + dj3
2 + dj3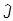 3] = i
3] = i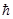 (dj2
(dj2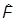 3-dj3
3-dj3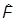 2).
2).
Сравниваем коэффициенты при dj1, а потом при dj2 :
[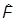 1,
1,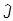 1]=0, [
1]=0, [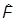 1,
1,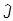 2] = i
2] = i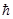
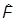 3.
3.
Остальные случаи получаются проектированием на оси 2 и 3, или циклической перестановкой индексов в выписанных соотношениях:
[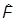 j,
j,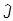 k] = i
k] = i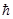 ejkl
ejkl 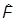 l.
l.
В частности, полагая  =
= ,получим коммутационные соотношения для компонентов самого момента:
,получим коммутационные соотношения для компонентов самого момента:
[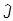 j,
j,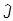 k] = i
k] = i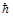 ejkl
ejkl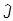 l.
l.
Так как  =
=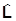 +
+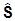 , [
, [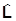 ,
,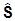 ]=
]=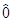 (действуют на разные переменные) и
(действуют на разные переменные) и
[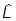 j,
j,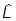 k] = i
k] = i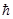 ejkl
ejkl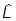 l
l
то для спиновых операторов получаем те же коммутационные соотношения, что и для орбитальных:
[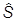 j,
j,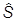 k] = i
k] = i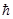 ejkl
ejkl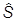 l.
l.
Если оператор F-скалярный, то абсолютно аналогичные рассуждения, основывающиеся на том, что при вращении dF = 0, дают
[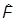 ,
,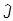 k] =
k] = 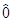 .
.
В частности, для квадратов полного момента и спина получаем
[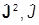 k] =
k] = 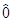 Þ [
Þ [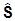 2,
2,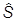 k]=
k]=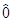
– Конец работы –
Эта тема принадлежит разделу:
ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА
РЕЗЮМЕ... стационарные состояния частицы в центральном поле характеризуются значениями... орбитальным азимутальным квантовым числом l...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МОМЕНТ ИМПУЛЬСА
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов