Быстрое преобразование Фурье

Быстрое преобразование Фурье (БПФ) - это не еще одна разновидность преобразования Фурье, а название целого ряда эффективных алгоритмов, предназначенных для быстрого вычисления дискретно-временного ряда Фурье. Основная проблема, возникающая при практической реализации ДВРФ, заключена в большом количестве вычислительных операций, пропорциональном N2. Хотя еще задолго до появления компьютеров было предложено несколько эффективных вычислительных схем, позволяющих существенно сократить число вычислительных операций, настоящую революцию произвела публикация в 1965 году статьи Кули (Cooly) и Тьюки (Tukey) c практическим алгоритмом быстрого (число операций Nlog₂N) вычисления ДВРФ. После этого было разработано множество вариантов, усовершенствований и дополнений основной идеи, составивших класс алгоритмов, известных под названием быстрого преобразования Фурье. Основная идея БПФ - деление N-точечного ДВРФ на два и более ДВРФ меньшей длины, каждый из которых можно вычислить отдельно, а затем линейно просуммировать с остальными, с тем чтобы получить ДВРФ исходной N-точечной последовательности.
Представим дискретное преобразование Фурье (ДВРФ) в виде

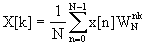, (35)

где величина W_N=exp(-j2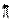/N) носит название поворачивающего множителя (здесь и далее в этом разделе период выборки T=1). Выделим из последовательности x[n] элементы с четными и нечетными номерами

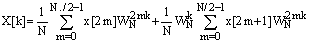. (36)

Но так как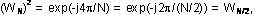 то
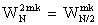. Следовательно, (36) можно записать в виде

, (37)

где каждое из слагаемых является преобразованием длины N/2

(38)

Заметим, что последовательность (WN/2)^nk периодична по k с периодом N/2. Поэтому, хотя номер k в выражении (37) принимает значения от 0 до N-1, каждая из сумм вычисляется для значений k от 0 до N/2-1. Можно оценить число комплексных операций умножения и сложения, необходимых для вычисления преобразования Фурье в соответствии с алгоритмом (37)-(38). Два N/2-точечных преобразования Фурье по формулам (38) предполагают выполнение 2(N/2)² умножений и приблизительно столько же сложений. Объединение двух N/2-точечных преобразований по формуле (37) требует еще N умножений и N сложений. Следовательно, для вычисления преобразования Фурье для всех N значений k необходимо произвести по N+N²/2 умножений и сложений. В то же время прямое вычисление по формуле (35) требует по N² умножений и сложений. Уже при N>2 выполняется неравенство N+N²/2 < N² , и, таким образом, вычисления по алгоритму (37)-(38) требуют меньшего числа математических операций по сравнению с прямым вычислением преобразования Фурье по формуле (35). Так как вычисление N-точечного преобразования Фурье через два N/2-точечных приводит к экономии вычислительных операций, то каждое из N/2-точечных ДПФ следует вычислять путем сведения их к N/4-точечным преобразованиям:

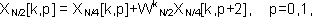, (39)
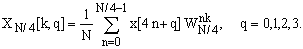(40)

При этом, вследствие периодичности последовательности W^nk_N/4 по k с периодом N/4, суммы (40) необходимо вычислять только для значений k от 0 до N/4-1. Поэтому расчет последовательности X[k] по формулам (37), (39) и (40) требует, как нетрудно подсчитать, уже по 2N+N²/4 операций умножения и сложения.
Следуя таким путем, объем вычислений X[k] можно все более и более уменьшать. После m=log₂N разложений приходим к двухточечным преобразованиям Фурье вида

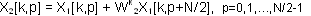(41)

где "одноточечные преобразования" X₁[k,p] представляют собой просто отсчеты сигнала x[n]:

X₁[k,q] = x[q]/N, q=0,1,...,N-1. (42)

В итоге можно записать алгоритм БПФ, получивший по понятным причинам название алгоритма с прореживанием по времени :

X₂[k,p] = (x[p] + W^k₂x[p+N/2]) / N,

где k=0,1, p=0,1,...,N/2 -1;

X_2N/M[k,p] =X_N/M[k,p] + W^k_2N/MX_N/M[k,p+M/2],

где k=0,1,...,2N/M -1, p=0,1,...,M/2 -1;

..X[k] = X_N[k] =X_N/2[k,0] + W^k_NX_N/2[k,1], (43)

где k=0,1,...,N-1

На каждом этапе вычислений производится по N комплексных умножений и сложений. А так как число разложений исходной последовательности на подпоследовательности половинной длины равно log₂N, то полное число операций умножения-сложения в алгоритме БПФ равно Nlog₂N. При больших N имеет место существенная экономия вычислительных операций по сравнению с прямым вычислением ДПФ. Например, при N = 2¹⁰ = 1024 число операций уменьшается в 117 раз.
Рассмотренный нами алгоритм БПФ с прореживанием по времени основан на вычислении преобразования Фурье путем формирования подпоследовательностей входной последовательности x[n]. Однако можно использовать также разложение на подпоследовательности преобразования Фурье X[k]. Алгоритм БПФ, основанный на этой процедуре, носит название алгоритма с прореживанием по частоте. Подробнее о быстром преобразовании Фурье можно прочитать, например, в [2].