СПЕКТР ДЛЯ ПРОЦЕССОВ
Спектр белого шума – константа (т.к.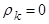 
для любого k>0, в данном случае это 2). Т.е. альтернативный вариант распознавания выхода на белый шум (в отличие от 
) – это изучение периодограммы остатков.
Вывод формулы, связывающей автоковариационную функцию и выборочный спектр.
Т.к. 
, то можно записать:
Воспользуемся выражением для 
:
Подставляя 
и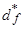 
в выражение для 
, получаем:
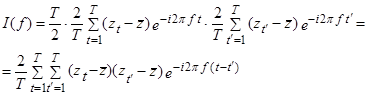
Вспомним, что эмпирическая автоковариация считается так:
и заменяя в 
на k:
[с учетом того, что 
и в силу симметричности можно написать] 
, т.е. разложим сумму на три части: (от (Т-1) до –1), она совпадает с суммой (от 1 до (Т-1)), и выделяем средний элемент 
.
Т.к. это выражение лежит в основе многих выкладок и результатов, то часто курс эконометрии начинается с этой формулы.
Итак, нормированный спектр и автокорреляционная функция в какой-то степени эквивалентны, следовательно, иногда удобно использоваться спектр, чтобы определить тип модели, а иногда удобно использовать автокорреляционную функцию. В нашем курсе основной инструмент для распознавания типа процесса – автокорреляционная функция.
Что делать, если мы переходим к непрерывным функциям, т.е. частоты измеряются не дискретно, а непрерывно?
Принцип остается тем же, а специфика заключается в том, что функция 
, если она непрерывна, не может быть представима в виде конечной суммы. Она представляется в виде бесконечной суммы, т.е. базис тоже является бесконечным. И разлагаем по этому базису.
Сложность в том, что не всякая функция может быть представлена в виде ряда Фурье, а только такая, для которой этот ряд сходится.
Вторая сложность в том, что когда мы определяем коэффициенты разложения Фурье: 
, т.е. совокупность гармоник 
, следовательно, переходим к интегралу, т.к. это непрерывная функция. Итак, в левой части получаем: 
, где t непрерывно изменяется от 0 до Т, а в правой части остается только один элемент: 
(или 
). И сложность состоит в том, чтобы зане6сти интеграл под сумму.
Но, в принципе, механизм остается тот же. Но нам это не надо, т.к. мы работаем с дискретными частотами и ВР.
Выборочный спектр и автокорреляционная функция связаны между собой следующим соотношением:
(*)
Если мы изучаем нормированный спектр, то для чисто случайного процесса это константа, равная 2.
Но мы изучаем периодограмму (т.е. выборочный, а не нормированный спектр), следовательно, критерий для остановки процесса построения модели в виде композиции существующих гармоник – выход на асимптотическую константу. Т.е. для случайного процесса выборочный спектр будет константой.
Вид выборочного спектра основных линейных процессов:
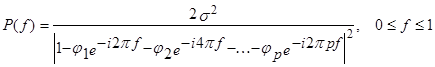
СПЕКТР ДЛЯ ПРОЦЕССОВ AR(p)
(дисперсия белого шума). Покажем это:
Эта функция получена из предыдущей, знаменатель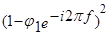 
преобразуется в знаменатель 
.
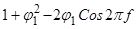Мы знаем, что для AR(1):
- дисперсия процесса
- автоковариация
Если их подставить в функцию спектра, то
у нас как раз 
, т.к. мы работаем со стационарными процессами
Выделяем элемент 
СПЕКТРЫ ПРОЦЕССОВ СКОЛЬЗЯЩЕГО СРЕДНЕГО MA(q)
СПЕКТРЫ АВТОРЕГРЕССИИ СКОЛЬЗЯЩЕГО СРЕДНЕГО ARMA(p,q)
ДИНАМИЧЕСКАЯ СПЕЦИФИКАЦИЯ РЕГРЕССИОННОЙ МОДЕЛИ
Лаг – запаздывание. Обычно под лагом понимают какую-то запаздывающую переменную.
Например, для переменной 
с лагом в 
периодов, такой лаговой переменной будет 
, хотя под лагом иногда подразумевается сама , а иногда структура.
В векторном виде луг записывают следующим образом: 
, т.е. все значения объединяются за весь период времени.
Очень удобно обозначать лаг с помощью лагового оператора, и если применить к вектору В, то 
.
Особенность темы в том, что мы выходим за рамки изучения одного ВР. Не всегда можно обойтись этими моделями. При введении в модель других объясняющих переменных модель усложняется.
МОДЕЛЬ РАСПРЕДЕЛЕННОГО ЛАГА
В модели на изменение исследуемой переменной y влияет не только какой-то объясняющий фактор х, но и его лаги. Тогда МРЛ можно записать так:
- в векторной форме, (1)
где 
, где q – величина максимального лага.
Коэффициенты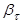 
показывают структуру лага и называются весами.
В случае мультиколлинеарности лаговых переменных обычно на лаговую структуру накладывают какое-нибудь ограничение, чтобы не уменьшать количество оцениваемых параметров.
ПОЛИНОМИАЛЬНЫЙ ЛАГ
(2)
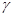- коэффициенты;
- степень многочлена.
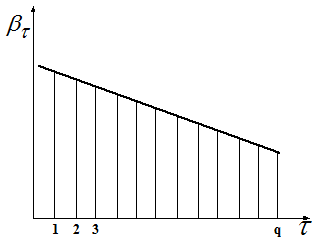
Простейший полиномиальный лаг – линейный, для которого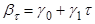 
.
Чтобы оценить такую модель, подставим выражение для 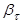в формулу (1), т.е. в исходную модель:
,
т.е. получается новая переменная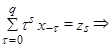 
(3)
где 
, т.е. 
- это преобразованные регрессоры, их значения всегда можно получить, следовательно, мы можем оценить значения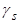 
методом наименьших квадратов. Подставив их в (2), найдем величину весов .
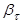ЭКСПОНЕНЦИАЛЬНЫЙ ЛАГ
(геометрический лаг)
Его веса задаются следующим соотношением: 
.
Т.е. веса геометрического лага убывают экспоненциально с увеличением лага, а не линейно.
В модели с геометрическим лагом можно применить преобразование Койка (Koyck transformation).
После этого преобразования модель с распределенным лагом будет выглядеть так:
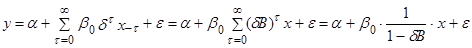(4)
(модель с экспоненциальной лаговой структурой после преобразования Койка)
(5)
Умножим обе части (4) на 
, зная, что если оператор сдвига стоит перед константой, то он ее сохраняет.
Проблема, которая возникает при оценивании модели распределенного лага – это определение величины наибольшего лага. Самый простой способ: взять модель с достаточно большим лагом и проверить гипотезы по отсечению хвоста с помощью t и F-статистик.
ДИНАМИЧЕСКИЕ РЕГРЕССИОННЫЕ МОДЕЛИ