рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Электроника
- /
- СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЯМИ
Реферат Курсовая Конспект
СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЯМИ
СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЯМИ - раздел Электроника, ЗАКОНЫ СОХРАНЕНИЯ Пусть ...
Пусть

Рассмотрим эрмитов оператор  (
(  ) такой, что
) такой, что
 ,
, 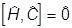 .
.
Построим однопараметрическое семейство операторов
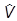 (a) = eia
(a) = eia .
.
Из эрмитовости  следует унитарность
следует унитарность 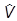 (a):
(a):
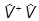 = eia
= eia e-ia
e-ia =
=  .
.
Из коммутативности  с
с  следует коммутативность
следует коммутативность 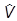 с
с  :
:

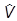 (a) =
(a) = 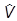 (a)
(a) ,
,
откуда, умножая слева на  и используя унитарность, найдем
и используя унитарность, найдем
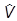 (a)
(a)
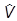 (a) =
(a) =  .
.
Таким образом, после совершения унитарного преобразования гамильтониан остается неизменным:
 =
=  .
.
Это и означает (собственно по определению), что в системе есть симметрия.
Важно, что все рассуждения можно обратить. Если 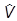 (a) - унитарное однопараметрическое преобразование, сохраняющее гамильтониан, то существует сохраняющаяся наблюдаемая, оператор которой находится как
(a) - унитарное однопараметрическое преобразование, сохраняющее гамильтониан, то существует сохраняющаяся наблюдаемая, оператор которой находится как
 =
=  .
.
Этот оператор эрмитов и коммутирует с гамильтонианом:
 ,
, 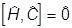 .
.
Пример. Рассмотрим систему с одной степенью свободы (координата x) и в качестве  возьмем оператор импульса:
возьмем оператор импульса:
 =
= 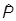 = -ii
= -ii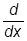 Þ
Þ  (a) = ei/i
(a) = ei/i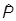 a = ead/dx.
a = ead/dx.
Посмотрим, как он действует на волновую функцию:
 (a)y (x) = ead/dx y(
(a)y (x) = ead/dx y( ) =
) =  y(x) =
y(x) = 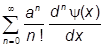 .
.
Но справа стоит разложение функции y (x+a) в ряд Тейлора по a. Таким образом, оператор  (a) есть оператор трансляции на a:
(a) есть оператор трансляции на a:
 y (x) = y (x+a).
y (x) = y (x+a).
Очевидно, что оператор  +(a) есть оператор трансляции на -a:
+(a) есть оператор трансляции на -a:
 +(a) y (x) = y (x-a).
+(a) y (x) = y (x-a).
В результате рассматриваемого преобразования операторы  наблюдаемых переходят в
наблюдаемых переходят в
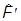 =
= +(a)
+(a)
 (a).
(a).
Найдем 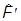 в явном виде, считая, что
в явном виде, считая, что  =
=  (x). Имеем:
(x). Имеем:
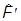 = y (x)
= y (x) (x)
(x)  (a) y (x) =
(a) y (x) =  +(a)(
+(a)( (x) y (x+a)) º
(x) y (x+a)) º +(a)j (x) =
+(a)j (x) =
= j (x-a) =  (x-a) y (x):
(x-a) y (x):
 +(a)
+(a) (x)
(x)  (a) =
(a) =  (x-a).
(x-a).
Если же  =
=  (
( ), то он коммутирует с
), то он коммутирует с (a), а потому не меняется:
(a), а потому не меняется:
 +(a)
+(a) (
( )
) (a) =
(a) = (
( ).
).
Обратные рассуждения (более важные) таковы. Пусть система трансляционно инвариантна. Это значит, что
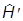 =
= +(a)
+(a)
 (a) =
(a) =  .
.
Так как
 (x),
(x),
то
 =
=  (x-a).
(x-a).
Инвариантность означает, что
U (x-a) = U (x),
т.е. потенциальная энергия не зависит от x. Она есть константа, которую можно положить равной нулю. Тем самым в данном случае результат получается достаточно тривиальным: трансляционно инвариантной является система, состоящая из одной свободной частицы. Сохраняющейся величиной будет
 =
=  =
=  ,
,
что в данном случае приводит к закону сохранения импульса.
– Конец работы –
Эта тема принадлежит разделу:
ЗАКОНЫ СОХРАНЕНИЯ
ЗАКОНЫ СОХРАНЕНИЯ В картине Шредингера затруднительно сразу сказать что такое сохраняющаяся...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЯМИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов