ПОТОК ОСВОБОЖДЕНИЙ И ЕГО МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Заявка (вызов) - это фактически требование источника на установление соединения, поступившее в коммутационную систему. Будем считать заявку обслуженной, если абонент получил соединение в пределах рассматриваемой коммутационной системы (КС). Различают при этом:

полностью обслуженный вызов - это когда произошло соединение с требуемым абонентом;

частично обслуженный вызов - когда соединение выполнено только на конкретном участке КС;

потерянный вызов - то есть не реализованный, получивший отказ из-за отсутствия в момент поступления свободных, доступных и исправных обслуживающих приборов (линий) или мест ожидания в очереди, а также занятости или неответа вызываемого абонента.

Вызовы, получившие неверное (ошибочное) соединение, также относят к потерянным.

Последовательность моментов окончания обслуживания вызовов образует поток освобождений (по подобию и аналогии с потоком вызовов). Свойства потока освобождений в общем случае зависят от свойств поступающего потока вызовов, качества работы КС как СМО, закона распределения времени обслуживания.

Длительность обслуживания заявки в КС может быть признана случайной величиной. Это объективно обусловлено самим случайным характером продолжительности телефонного разговора, возможностью поступления заявки на соединение уже с занятым или отсутствующим абонентом, ошибками установления соединения. Перечисленные ситуации предполагают занятие в КС обслуживающих приборов (ОП).

Вероятность того, что случайное время обслуживания Т поступившей в систему заявки не превысит величинуτ полагают обычно подчиненной показательному закону распределения:

P(Т< τ) = 1 – e^-,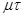

где= 1/Тср - интенсивность обслуживания;

Тср - среднее время обслуживания.

Обычно в телефонии для внутренней связи значение среднего времени обслуживания Тср принимают равным 3 мин., для дальней связи - 5 мин.

Вероятность того, что за время τ занятый обслуживанием заявки ОП не освободится:

P(Т>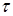) = 1 – Р(Т<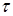) = e^-.

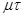При рассмотрении малого интервала , когда τ <<1, вероятность того, что прибор занят обслуживанием:

P(Т>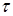) = Р₃ 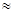1 – .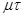

При наличии в системе ровно k занятых приборов вероятность, что ни один из них не освободится, равна

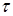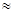Р_3к()+ е^-1-.

Гипотеза о показательном законе распределения интервала между поступающими заявками, равно как и длительности обслуживания заявки, значительно упрощает применяемый математический аппарат анализа КС как СМО и при этом позволяет получить ценные для практики результаты оценки эффективности работы телефонных станций.